
3.1 图像的几何变换 ¤灰度插值: ()最近邻插值法:也称作零阶插值,就是令变换后像素的灰度 值等于距它最近的输入像素的灰度值。 特点:造成的空间偏移误差为1/√2像素单位,计算简单。但当图像中 的像素灰度级有细微变化时,该方法会在图像中产生人工的痕迹。 (②)双线性插值:也称作一阶插值,该方法通常是沿图像矩阵的每 一列(行)进行插值,然后对插值后所得到的矩阵再沿着行 (列)方向进行线性插值。 特点:当对相邻四个像素点采用双线性插值时,所得表面在邻域处是吻 合的,但斜率不吻合。并且双线性灰度插值的平滑作用可能使得图像的细节 产生退化,这种现象在进行图像放大时尤其明显。 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 ◘灰度插值 : (1) 最近邻插值法: 最近邻插值法:也称作零阶插值,就是令变换后像素的灰度 也称作零阶插值,就是令变换后像素的灰度 值等于距它最近的输入像素的灰度值。 值等于距它最近的输入像素的灰度值。 特点:造成的空间偏移误差为 像素单位,计算简单。但当图像中 的像素灰度级有细微变化时,该方法会在图像中产生人工的痕迹。 (2)双线性插值: 也称作一阶插值 也称作一阶插值,该方法通常是沿图像矩阵的每 该方法通常是沿图像矩阵的每 一列(行)进行插值,然后对插值后所得到的矩阵再沿着行 一列(行)进行插值,然后对插值后所得到的矩阵再沿着行 (列)方向进行线性插值。 (列)方向进行线性插值。 特点:当对相邻四个像素点采用双线性插值时,所得表面在邻域处是吻 合的,但斜率不吻合。并且双线性灰度插值的平滑作用可能使得图像的细节 产生退化,这种现象在进行图像放大时尤其明显。 2/1

3.1 图像的几何变换 灰度插值: (③)卷积插值法:当图像放大时,图像像素的灰度值插值可以通 过卷积来实现,即将输入图像两行两列中间插零值,然后通过低 通模板滤波。 X11 0x12 X11 X12 0 00 X21 X22 X21 0x22」 输入图像邻域 插零的邻域 一般低通模板有: 「1 33 17 1 4 6 4 1 2 4 16 24 16 4 1 1 3 9 9 3 1 2 4 2 6 36 6 1 4 3 9 9 3 64 4 16 24 16 4 1 21 331 1 4 6 4 柱形 棱锥形 钟形 三次B样条 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 ◘灰度插值 : (3)卷积插值法 :当图像放大时,图像像素的灰度值插值可以通 当图像放大时,图像像素的灰度值插值可以通 过卷积来实现,即将输入图像两行两列中间插零值,然后通过低 过卷积来实现,即将输入图像两行两列中间插零值,然后通过低 通模板滤波。 输入图像邻域 插零的邻域 一般低通模板有: 一般低通模板有: 柱形 棱锥形 钟形 三次B样条 ⎥⎦⎤ ⎢⎣⎡ 2221 1211 xx xx ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ 21 22 11 12 0 000 0 xx xx ⎥⎦⎤ ⎢⎣⎡ 11 11 ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ 121 242 121 41 ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ 1331 3993 3993 1331 161 ⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎣⎡ 14641 41624164 62436246 41624164 14641 641
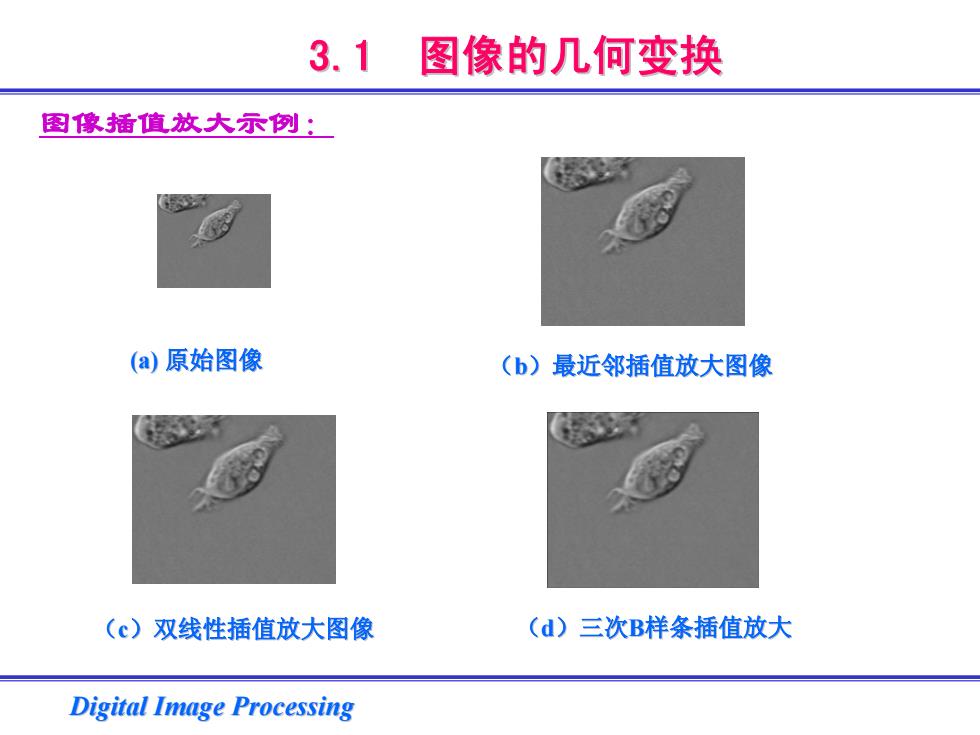
3.1 图像的几何变换 图像插值放大示例: (a)原始图像 (b)最近邻插值放大图像 (c)双线性插值放大图像 (d)三次B样条插值放大 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 (a) 原始图像 (b)最近邻插值放大图像 (c)双线性插值放大图像 (d)三次B样条插值放大 图像插值放大示例:
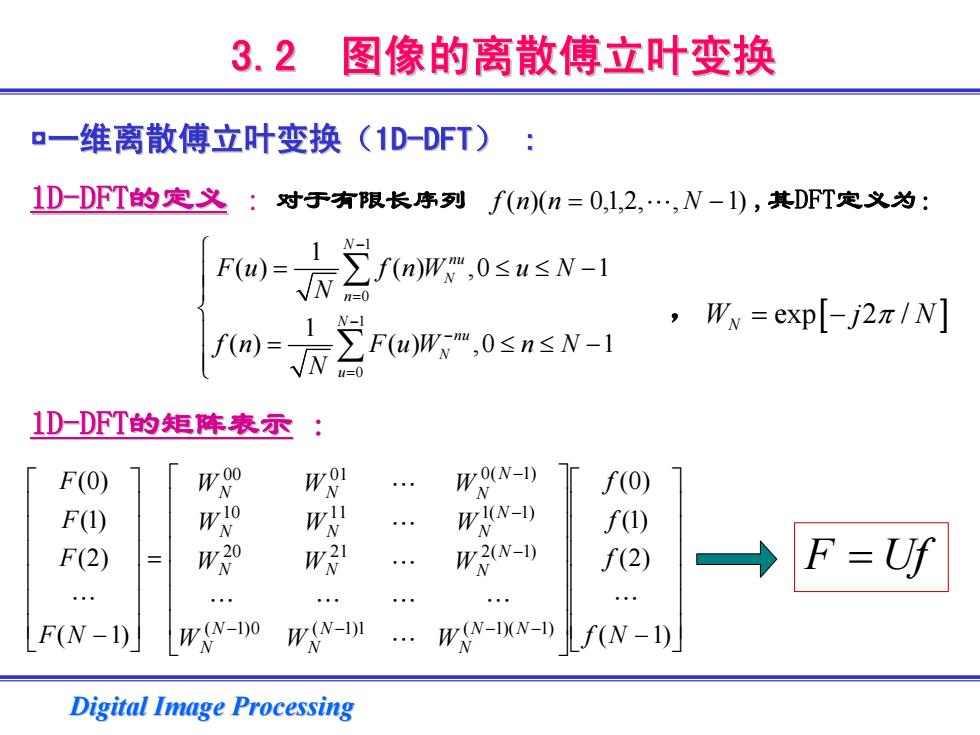
3.2 图像的离散傅立叶变换 o一维离散傅立叶变换(1D-DFT): 1D-DFT的定义:对于有限长序列f(n)(n=0,l,2,,N-I),其DFT定义为: w=∑/0mwW,0susN =2o05asN- N-1 ,W=exp[-j2π/N] 1D-DFT的矩阵表示: F(0) W E9- f(0) F(I) WAo W WJ(N-D f四) F(2) m20 … P2N-) f(2) →F=Uf F(N-1) WXN-10 WN-DI WXN-DXN-D) f(N-1) Digital Image Processing
Digital Image Processing Digital Image Processing 3.2 图像的离散傅立叶变换 图像的离散傅立叶变换 ◘一维离散傅立叶变换( 一维离散傅立叶变换(1D-DFT) : 1D-DFT的定义 :对于有限长序列 ,其DFT定义为: , 1D-DFT的矩阵表示 : nnf = " N − )1,,2,1,0)(( 1 0 1 0 1 ( ) ( ) ,0 1 1 ( ) ( ) ,0 1 N nu N n N nu N u F u f nW u N N f n F uW n N N − = − − = ⎧ = ≤≤ − ⎪⎪⎨⎪ = ≤≤ − ⎪⎩ ∑∑ ⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎣⎡ − ⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎣⎡ = ⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎣⎡ − − − −− −−− )1( )2( )1( )0( )1( )2( )1( )0( 1)1(0)1( )1)(1( 20 21 )1(2 10 11 )1(1 00 01 )1(0 Nf fff W W W WW W WW W WW W NF FFF NNN NN NN N N N N N N N N N N N N " " " """ """ " = UfF W jN N = − exp 2 / [ π ]

3.2 图像的离散傅立叶变换 其中: F=F(0 F(1)F(2)· F(N-1) f=[f(o)fa)f(2) … f(N-1)] W Wo(N-D U= W W Wj(N-D ·· W(N-10 W(W-DI W(N-1XN-1) 其中的U称为变换矩阵。从U的构成形式可知,U是对称的,即 U"=U 又由U(U*)T=IN,则U称为酉矩阵,且U1=(U*)T=U*, 而1D-DFT就称为正交变换。 同理可得到反变换的矩阵表示: f=U-F=U*F Digital Image Processing
Digital Image Processing Digital Image Processing 3.2 图像的离散傅立叶变换 图像的离散傅立叶变换 其中: , , 其中的 称为变换矩阵。从 的构成形式可知, 是对称的,即 又由 ,则 称为酉矩阵,且 , 而1D-DFT就称为正交变换。 同理可得到反变换的矩阵表示: [ ]T = FFFF " NF − )1()2()1()0( 00 01 0( 1) 10 11 1( 1) ( 1)0 ( 1)1 ( 1)( 1) N NN N N NN N N N NN NN N WW W WW W U WW W − − − − −− ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ "" " "" " " [ ]T = " Nfffff − )1()2()1()0( U U U UU T = N T *)( = IUU U **)( 1 UUU T == − * FUFUf 1 == −