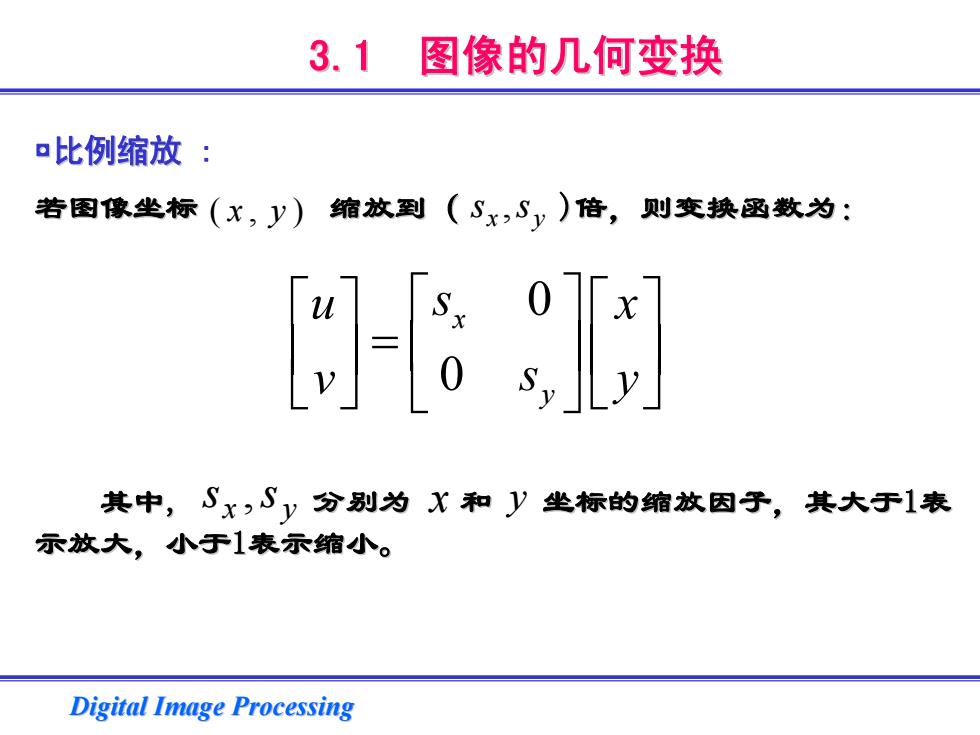
3.1 图像的几何变换 比例缩放: 若图像坐标(X,y)缩放到(Sx,y)倍,则变换函数为: 其中,Sx,Sy分别为X和y坐标的缩放因子,其大于1表 示放大,小于1表示缩小。 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 ◘比例缩放 : 若图像坐标 缩放到( )倍,则变换函数为: 倍,则变换函数为: 其中, , 分别为 和 坐标的缩放因子,其大于 坐标的缩放因子,其大于1表 示放大,小于1表示缩小。 yx ),( yx ,ss 0 0 x y u x s v s y ⎡ ⎤ ⎡⎤ ⎡ ⎤ ⎢ ⎥ ⎢⎥ = ⎢ ⎥ ⎣ ⎦ ⎣⎦ ⎣ ⎦ yx ,ss x y
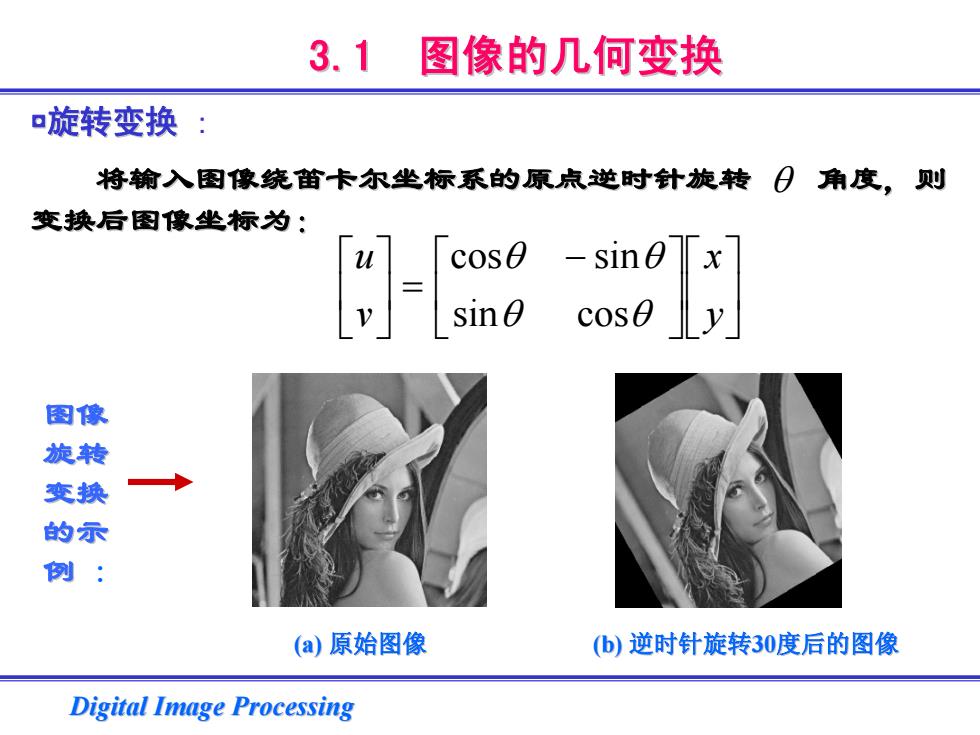
3.1 图像的几何变换 旋转变换: 将输入图像绕笛卡尔坐标系的原点逆时针旋转日角度,则 变换后图像坐标为: 图像 旋转 变换 的示 例: (a)原始图像 (b)逆时针旋转30度后的图像 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 ◘旋转变换 : 将输入图像绕笛卡尔坐标系的原点逆时针旋转 将输入图像绕笛卡尔坐标系的原点逆时针旋转 角度,则 变换后图像坐标为: 变换后图像坐标为: θ ⎥⎦⎤ ⎢⎣⎡⎥⎦⎤ ⎢⎣⎡ − ⎥ = ⎦⎤ ⎢⎣⎡ yx vu θθ θθ cossin sincos 图像 旋转 变换 的示 例 : (a) 原始图像 (b) 逆时针旋转30度后的图像

3.1 图像的几何变换 仿射变换 u 仿射变换的一般表达式为: a, a b2 y b bo 1 平移、比例缩放和旋转变换都是一种称为仿射变换的特殊情况。 仿射变换具有如下性质: (1)仿射变换只有6个自由度(对应变换中的6个系数),因 此,仿射变换后互相平行直线仍然为平行直线,三角形映射后仍 是三角形。但却不能保证将四边形以上的多边形映射为等边数的 多边形。 (2)仿射变换的乘积和逆变换仍是仿射变换。 (3)仿射变换能够实现平移、旋转、缩放等几何变换。 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 ◘仿射变换 : 仿射变换的一般表达式为 仿射变换的一般表达式为: 平移、比例缩放和旋转变换都是一种称为仿射变换的特殊情况。 210 210 1 x u aaa y v bbb ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎢ ⎥ ⎣ ⎦ 仿射变换具有如下性质 仿射变换具有如下性质: (1)仿射变换只有 )仿射变换只有6个自由度(对应变换中的 个自由度(对应变换中的6个系数),因 此,仿射变换后互相平行直线仍然为平行直线,三角形映射后仍 此,仿射变换后互相平行直线仍然为平行直线,三角形映射后仍 是三角形。但却不能保证将四边形以上的多边形映射为等边数的 是三角形。但却不能保证将四边形以上的多边形映射为等边数的 多边形。 (2)仿射变换的乘积和逆变换仍是仿射变换。 )仿射变换的乘积和逆变换仍是仿射变换。 (3)仿射变换能够实现平移、旋转、缩放等几何变换。 )仿射变换能够实现平移、旋转、缩放等几何变换

3.1图像的几何变换 上式可以表示成如下的线性表达式 设定加权因于☑;和b:的值,可以得到不同的变换。例如,当选定 a2=b=1,b2=-0.1,41=a40=b0=0,该情况是图像剪切的一种到剪 切。 (a)原始图像 (b)仿射变换后图像 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 上式可以表示成如下的线性表达式 上式可以表示成如下的线性表达式 : 设定加权因子 和 的值,可以得到不同的变换。例如,当选定 , , ,该情况是图像剪切的一种列剪 切。 (a)原始图像 (b)仿射变换后图像 ⎥⎦⎤ ⎢⎣⎡ ⎥ +⎦⎤ ⎢⎣⎡⎥⎦⎤ ⎢⎣⎡ ⎥ =⎦⎤ ⎢⎣⎡ 00 12 12 ba yx bb aa vu ai bi = ba 12 = 1 b2 −= 1.0 0 = = baa 001 =
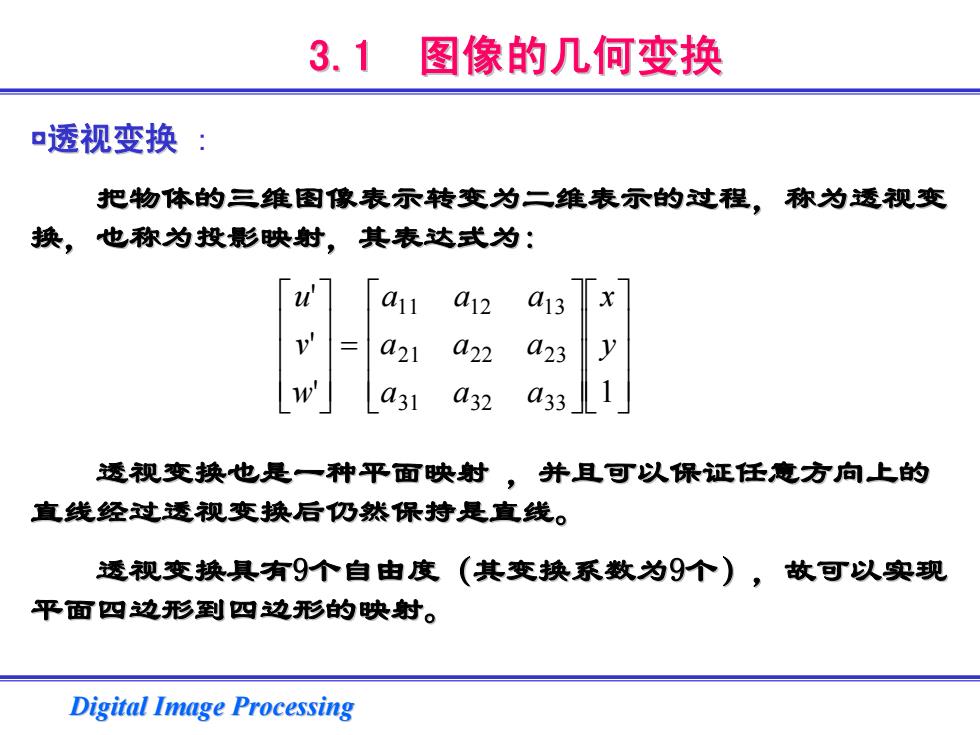
3.1 图像的几何变换 透视变换: 把物体的三维图像表示转变为二维表示的过程,称为透视变 换,也称为投影映射,其表达式为: C11 a12 a13 a21 a22 023 w a31 a32 033 透视变换也是一种平面映射,并且可以保证任意方向上的 直线经过透视变换后仍然保持是直线。 透视变换具有9个自由度(其变换系数为9个),故可以实现 平面四边形到四边形的映射。 Digital Image Processing
Digital Image Processing Digital Image Processing 3.1 图像的几何变换 图像的几何变换 ◘透视变换 : 把物体的三维图像表示转变为二维表示的过程,称为透视变 把物体的三维图像表示转变为二维表示的过程,称为透视变 换,也称为投影映射,其表达式为 换,也称为投影映射,其表达式为: 透视变换也是一种平面映射 透视变换也是一种平面映射 ,并且可以保证任意方向上的 ,并且可以保证任意方向上的 直线经过透视变换后仍然保持是直线。 直线经过透视变换后仍然保持是直线。 透视变换具有9个自由度(其变换系数为 个自由度(其变换系数为9个),故可以实现 个),故可以实现 平面四边形到四边形的映射。 平面四边形到四边形的映射。 ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ =⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ ' 1 '' 333231 232221 131211 yx aaa aaa aaa wvu