
压杆稳定$13.2细长压杆的临界压力一、两端铰支压杆的临界压力假定压力已达到临界值,杆已经处于微弯状态,如图从挠曲线入手,求临界压力。①弯矩: M(x,y)=-PyP2Ax②挠曲线近似微分方程:PM1LMEIEIPy=y"+k?y=0DhPETJXp其中k2EI
§13.2 细长压杆的临界压力 一、两端铰支压杆的临界压力: M (x, y) = −Py 假定压力已达到临界值,杆已经处于微弯状态,如图, 从挠曲线入手,求临界压力。 y EI P EI M y = = − ①弯矩: ②挠曲线近似微分方程: 0 2 + y=y +k y= EI P y EI P k = 2 其中: P P x

压杆稳定③微分方程的解:y=Asin x+ Bcosx④确定积分常数:y(0)-y(L)-00Ax0+B=00即sinkL coskLAsin kL+BcoskL-oP.:hnr.. sinkL-0LVEI临界力 P是微弯下的最小压力,故,只能取n-1;且杆将绕惯性矩最小的轴弯曲。..P.元"ElmnL?
③微分方程的解: ④确定积分常数: y=Asin x+Bcosx y(0)=y(L)=0 + = + = sin cos 0 0 0 : A k L B k L A B 即 0 sin cos 0 1 = k L k L sinkL=0 EI P L n k= = 临界力 Pcr 是微弯下的最小压力,故,只能取n=1 ;且 杆将绕惯性矩最小的轴弯曲。 2 min 2 L EI Pcr =

压杆稳定_元ElminPL2两端铰支细长压杆临界力的欧拉公式此公式的应用条件:1. 理想压杆;2.线弹性范围内:3.两端为球铰支座
此公式的应用条件: 1.理想压杆; 2.线弹性范围内; 3.两端为球铰支座。 ——两端铰支细长压杆临界力的欧拉公式 2 2 L EI Pcr min =

压杆稳定二、其他支座条件下压杆的临界压力其他约束情况下,分析方法与两端铰支的相同其它支承情况下,压杆临界力为,_元EImin(μuL)?压杆临界力欧拉公式的一般形式μ-长度系数(或约束系数)
—长度系数(或约束系数)。 压杆临界力欧拉公式的一般形式 2 2 ( ) min L EI Pcr = 其它支承情况下,压杆临界力为 其他约束情况下,分析方法与两端铰支的相同 二、其他支座条件下压杆的临界压力
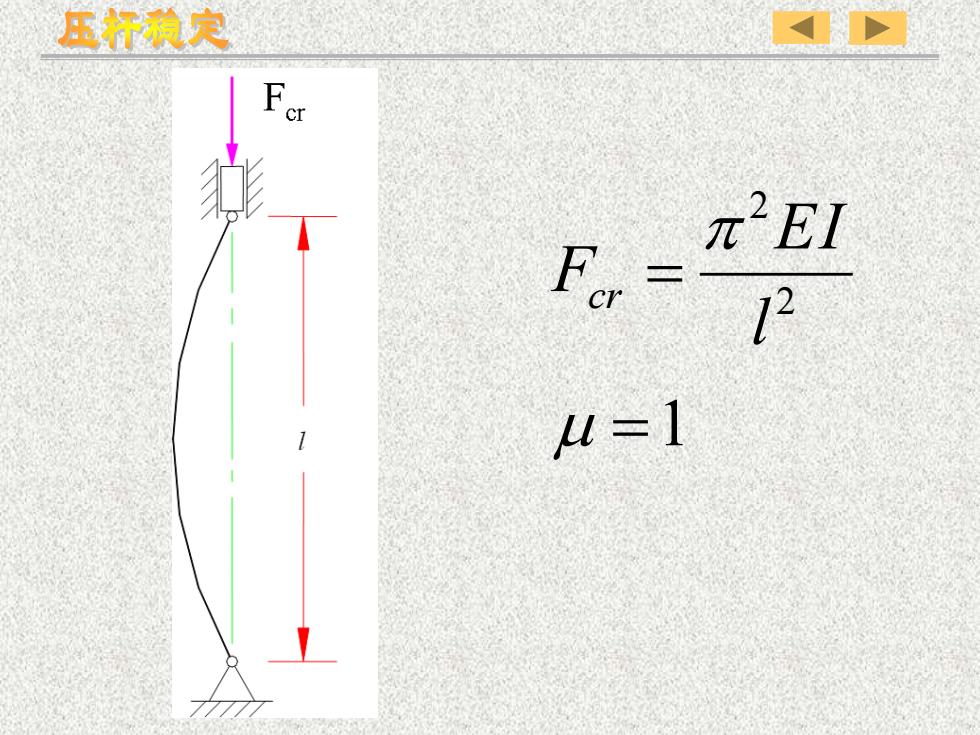
压杆稳定F.a元EI家Fer-12u=1
1 2 2 = = l EI Fcr