
5.2.4.凸优化问题 ·凸优化问题是指约束最优化问题 min f(w) s.t. 8(w)≤0,i=1,2,..,k h(w)=0,i=1,2,..,1 ·目标函数f(w)和约束函数g(w)都是R”上的连续 可微的凸函数,h,(w)是R”上的仿射函数。 。当目标函数f(w)是二次函数,且约束函数g(w)是 仿射函数时,成为凸二次规划问题。 ·注意:带约束条件凸函数成立条件:(1)目标函数是凸函数;(2) 约束条件是凸集。我们将在后面证明此处的约束条件是凸集。 20/154
5.2.4. 凸优化问题 ▶ 凸优化问题是指约束最优化问题: min w f (w) s.t. gi(w) ≤ 0, i = 1, 2, . . . , k hi(w) = 0, i = 1, 2, . . . , l 目标函数 f (w) 和约束函数 gi(w) 都是 R n 上的连续 可微的凸函数, hi(w) 是 R n 上的仿射函数。 当目标函数 f (w) 是二次函数,且约束函数 gi(w) 是 仿射函数时,成为凸二次规划问题。 ▶ 注意:带约束条件凸函数成立条件:(1)目标函数是凸函数;(2) 约束条件是凸集。我们将在后面证明此处的约束条件是凸集。 20 / 154

凸函数 ·如果连接任意在集合C内两点的线段依然在C内,则 集合C称为凸集。对任意x1,x2∈C,0≤0≤1,我们有: 0x1+(1-0)x2∈C. ·函数f:R”→R称为凸函数,如果dom(f)(自变量取值 范围)是一个凸集,且对于所有x,y∈dom(),0≤9≤1, 有: f(0x+(1-8)y)≤0f(x)+(1-0)fy) 定义域上的加权平均的函数小于等于值域上的加权平均 。如果-f(x)是凸函数,则称(x)为凹函数。 如果函数f:R”→Rm是一些线性函数和常数之和,称 为仿射(affine)函数。 f(x)=Ax+b,A∈Rmxm,b∈Rm 21/154
凸函数 ▶ 如果连接任意在集合 C 内两点的线段依然在 C 内,则 集合 C 称为凸集。对任意 x1, x2 ∈ C, 0 ≤ θ ≤ 1 , 我们有: θx1 + (1 − θ)x2 ∈ C. ▶ 函数 f : R n → R 称为凸函数,如果 dom( f ) (自变量取值 范围)是一个凸集,且对于所有 x, y ∈ dom( f ), 0 ≤ θ ≤ 1 , 有: f (θx + (1 − θ)y) ≤ θf (x) + (1 − θ)f (y) ▶ 定义域上的加权平均的函数小于等于值域上的加权平均 ▶ 如果 − f (x) 是凸函数,则称 f (x) 为凹函数。 ▶ 如果函数 f : R n → R m 是一些线性函数和常数之和,称 为仿射 (affine) 函数。 f (x) = Ax + b, A ∈ R m×n , b ∈ R m 21 / 154
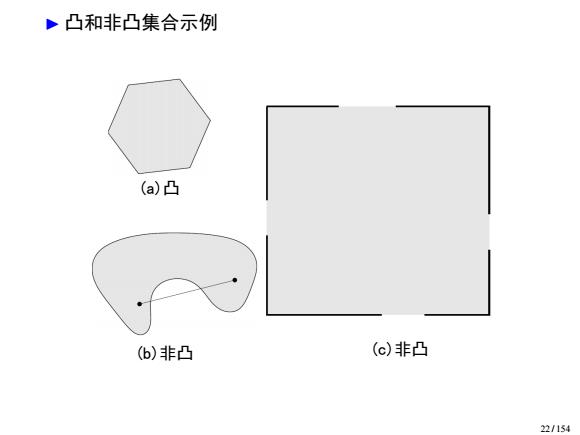
·凸和非凸集合示例 (a)凸 (6)非凸 (c)非凸 22/154
▶ 凸和非凸集合示例 文泉(计算机学院) 凸优化简介 (a)凸 (b)非凸 (c)非凸 22 / 154
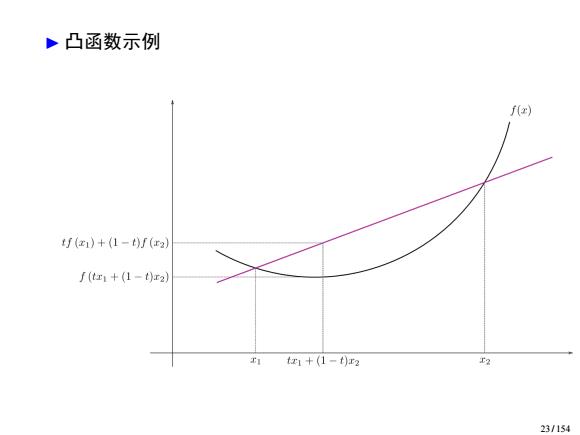
·凸函数示例 f() j(z1)+(1-t)f(r2) ∫(t红1+(1-t)x2】 tx1+(1-)2 T2 23/154
▶ 凸函数示例 23 / 154

凸函数的判断 f(y) f(x)+Vf(a)T(y-x) (x.f()) First-order conditions:Suppose fis differentiable(i.e.,its gradient Vfexists at each point in dom(f),which is open). Then f is convex if and only if: ①dom(f)is convex 2fy)≥f(x)+f(x)Ty-x),x,y∈dom(f) First order Taylor expansion approximation 24/154
凸函数的判断 ▶ First-order conditions: Suppose f is differentiable (i.e., its gradient ∇f exists at each point in dom( f ), which is open). Then f is convex if and only if: 1 dom( f ) is convex 2 f (y) ≥ f (x) + ∇f (x) T (y − x), ∀x, y ∈ dom( f ) First order Taylor expansion approximation 24 / 154