
·一般地,当训练数据集线性可分时,存在无穷个分离超 平面可将两类数据正确分开。 ·感知机利用误分类最小的策略,求得分离超平面。这时, 解有无穷多个。 ·线性可分支持向量机利用间隔最大化,求最优分离超平 面。这时,解是唯一的 10/154
▶ —般地,当训练数据集线性可分时,存在无穷个分离超 平面可将两类数据正确分开。 ▶ 感知机利用误分类最小的策略,求得分离超平面。这时, 解有无穷多个。 ▶ 线性可分支持向量机利用间隔最大化,求最优分离超平 面。这时,解是唯一的. 10 / 154

SVM的分类 支持向量机(Support Vector Machine,.SVM)模型可分为: 线性可分SVM(linear SVM in linearly separable case)。当 训练数据线性可分时,采用硬间隔最大化(hard margin maximization),学习线性的分类器,即线性可分SVM,又称 为硬间隔SVM; ·线性SVM(linear SVM)。当训练数据近似线性可分时, 通过软间隔最大化(soft margin maximization),也学习一个 线性的分类器,即线性SVM,又称为软间隔$VM ·非线性SVM(non--linear SVM)。当训练数据线性不可分 时,通过使用核技巧(kernel trick)及软间隔最大化,学习非 线性SVM。 ·简单模型是复杂模型的基础,也是复杂模型的特殊情况, 11/154
SVM 的分类 支持向量机 (Support Vector Machine, SVM) 模型可分为: ▶ 线性可分SVM(linear SVM in linearly separable case)。当 训练数据线性可分时,采用硬间隔最大化(hard margin maximization), 学习线性的分类器,即线性可分 SVM,又称 为硬间隔SVM; ▶ 线性 SVM(linear SVM)。当训练数据近似线性可分时, 通过软间隔最大化(soft margin maximization),也学习一个 线性的分类器,即线性 SVM,又称为软间隔SVM. ▶ 非线性 SVM(non-linear SVM)。当训练数据线性不可分 时,通过使用核技巧 (kernel trick) 及软间隔最大化,学习非 线性 SVM。 ▶ 简单模型是复杂模型的基础,也是复杂模型的特殊情况. 11 / 154
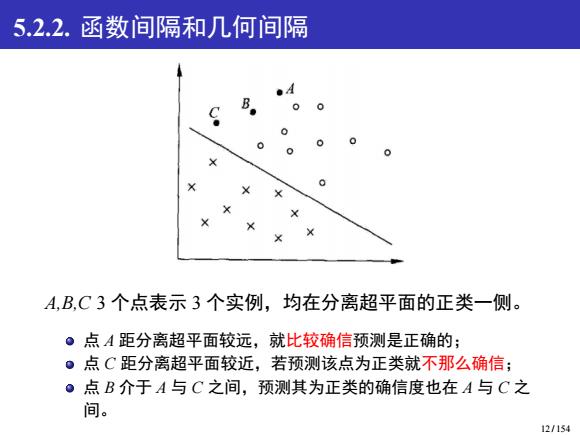
5.2.2.函数间隔和几何间隔 A,B,C3个点表示3个实例,均在分离超平面的正类一侧。 ●点A距分离超平面较远,就比较确信预测是正确的; ·点C距分离超平面较近,若预测该点为正类就不那么确信; ●点B介于A与C之间,预测其为正类的确信度也在A与C之 间。 12/154
5.2.2. 函数间隔和几何间隔 A,B,C 3 个点表示 3 个实例,均在分离超平面的正类一侧。 点 A 距分离超平面较远,就比较确信预测是正确的; 点 C 距分离超平面较近,若预测该点为正类就不那么确信; 点 B 介于 A 与 C 之间,预测其为正类的确信度也在 A 与 C 之 间。 12 / 154

函数间隔 ·一般来说,一个点距离分离超平面的远近可以表示分类 预测的确信程度 函数间隔(functional margin). 对于给定的训练数据集T和超平面(w,b),定义 ·超平面(w,b)关于样本点(x,)的函数间隔为: :=y(w·x+b) ·超平面(w,b)关于训练数据集T的函数间隔为: Y=min i=1,N 13/154
函数间隔 ▶ 一般来说,一个点距离分离超平面的远近可以表示分类 预测的确信程度. ▶ 函数间隔 (functional margin) 对于给定的训练数据集 T 和超平面 (w, b) ,定义 超平面 (w, b) 关于样本点 (xi , yi) 的函数间隔为: γˆi = yi(w · xi + b) 超平面 (w, b) 关于训练数据集 T 的函数间隔为: γˆ = min i=1,..., N γˆi 13 / 154

·函数间隔可以表示分类预测的正确性及确信度。但是选 择分离超平面时,只有函数间隔还不够。 只要成比例地改变w和b,例如将它们改为2w和2b, 超平面并没有改变,但函数间隔却成为原来的2倍。 ·可以对分离超平面的法向量加某些约束,如规范化, llwll =1 使得间隔是确定的。这时函数间隔成为几何间隔(geometric margin). 14/154
▶ 函数间隔可以表示分类预测的正确性及确信度。但是选 择分离超平面时,只有函数间隔还不够。 ▶ 只要成比例地改变 w 和 b , 例如将它们改为 2w 和 2b , 超平面并没有改变,但函数间隔却成为原来的 2 倍。 ▶ 可以对分离超平面的法向量 w 加某些约束,如规范化, kwk = 1 使得间隔是确定的。这时函数间隔成为几何间隔(geometric margin)。 14 / 154