
②过渡区或阿伦定律区(Allen) (2<Rep<500) 18.5 (5-7) 4,0.27 gde Yp Y 阿伦公式 ③湍流区或牛顿定律区(Nuton) (500<Rep<2x105) 10.44 (5-8) dpY。Yg (5-20) 4,1.74, 一牛顿公式 Y
0.6 Re 18.5 p 0.6 Re 0.27 p p p t gd u ——阿伦公式 ③ 湍流区或牛顿定律区(Nuton)(500<Rep < 2×105 ) 0.44 d g u p p t 1.74 ——牛顿公式 ② 过渡区或阿伦定律区(Allen)(2<Rep<500) (5-7) (5-8) (5-20)
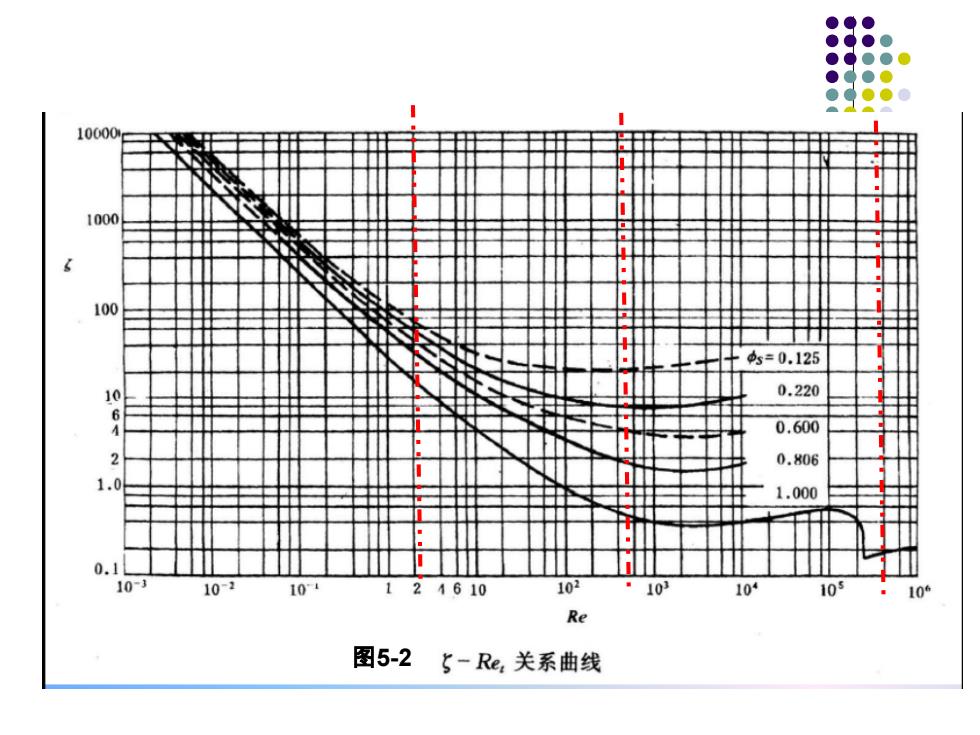
10000 1000 100 s=0.125 10 0.220 6 0.600 0.806 1.000 0.1 103 102 104 24610 102 0 10 109 Re 图5-25-Re,关系曲线
图5-2
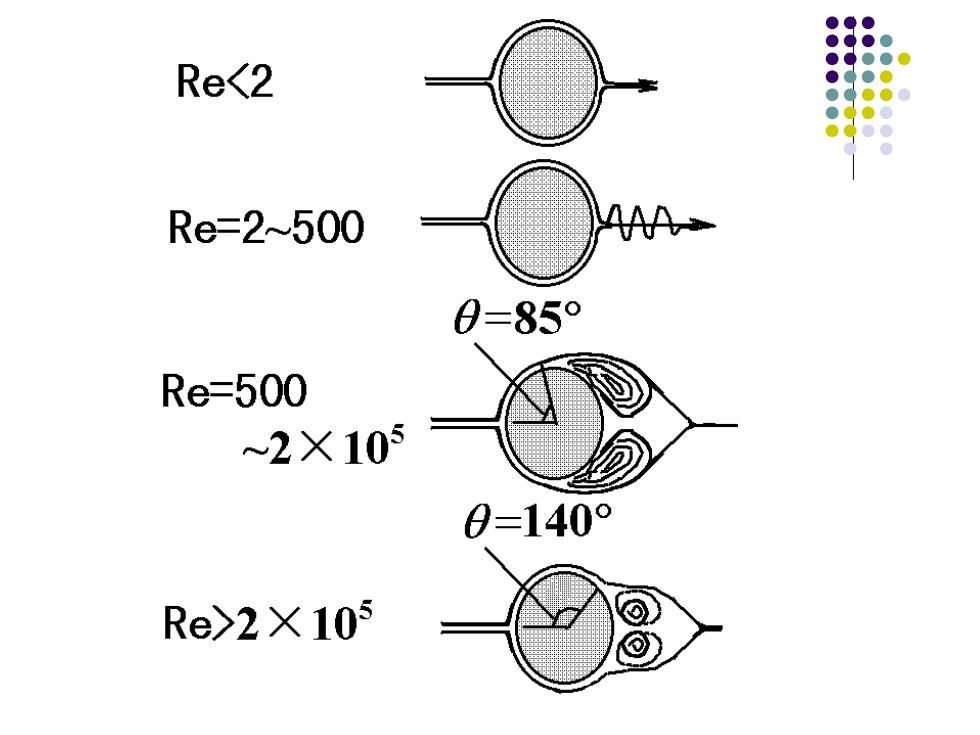
Re<2 Re=2~500 AAA 0=85° Re=500 ~2X105 0=140° Re>2X105

u,是颗粒与流体的综合特性。 u采用了极限处理方法 2.加速过程的地位 是否重要,要予以判断 大颗粒,加速时间长,走过距离长, 几乎一直在加速。 小颗粒,加速时间短,走 0.996 加速段可忽略。 稳定过程 加速过程 T
ut是颗粒与流体的综合特性。 ut采用了极限处理方法 2.加速过程的地位 是否重要, 要予以判断 大颗粒,加速时间长,走过距离长, 几乎一直在加速。 小颗粒,加速时间短,走过距离短, 加速段可忽略
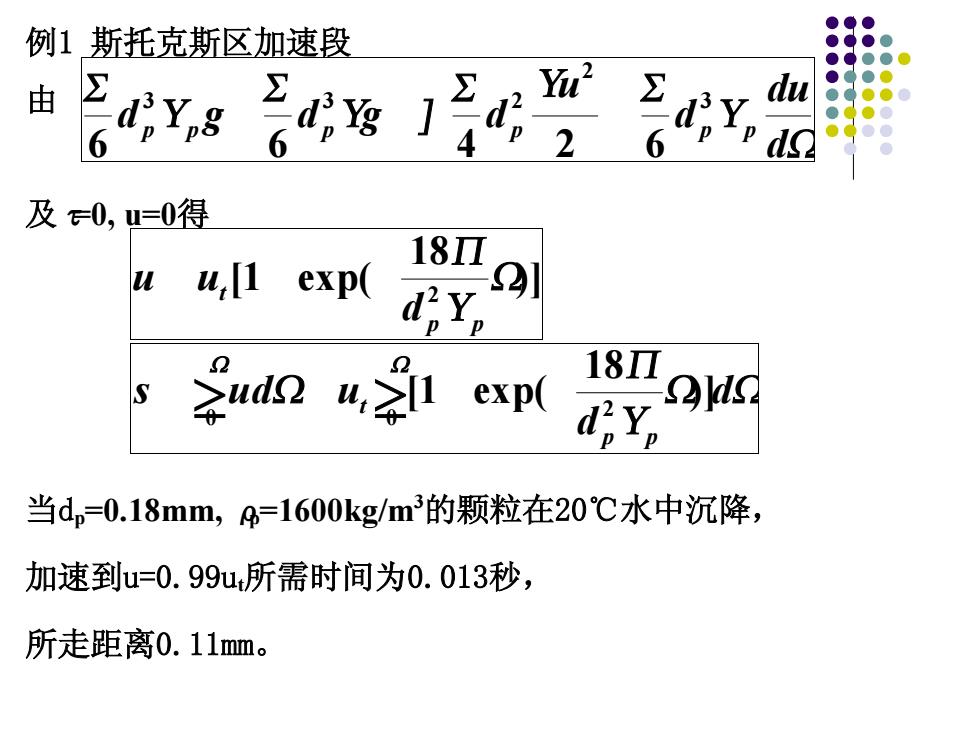
例1斯托克斯区加速段 由 du 6 02 6 及0,=0得 18Π wu,[1 exp( exp( 18立01 当dp=0.18mm,4=1600kgm3的颗粒在20℃水中沉降, 加速到u=0.99u所需时间为0.013秒, 所走距离0.11mm
例1 斯托克斯区加速段 由 及τ=0, u=0得 当dp=0.18mm, ρp=1600kg/m3 的颗粒在20℃水中沉降, 加速到u=0.99ut所需时间为0.013秒, 所走距离0.11mm。 d du d u d g d g d p p p p p p 3 2 3 3 2 6 6 4 2 6 )] 18 [1 exp( 2 p p t d u u d d s ud u p p t 0 2 0 )] 18 [1 exp(