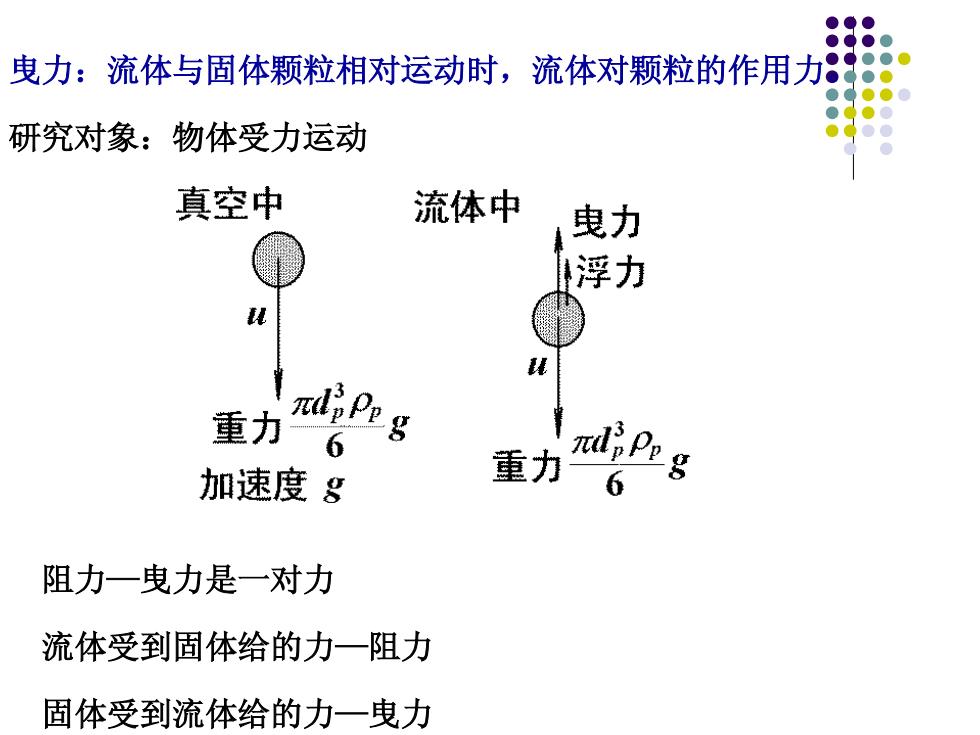
曳力:流体与固体颗粒相对运动时,流体对颗粒的作用力8 研究对象:物体受力运动 真空中 流体中 曳力 浮力 重力 lPeg 6 加速度g 重力 πd品Pg 6 阻力一曳力是一对力 流体受到固体给的力一阻力 固体受到流体给的力一曳力
阻力—曳力是一对力 流体受到固体给的力—阻力 固体受到流体给的力—曳力 曳力:流体与固体颗粒相对运动时,流体对颗粒的作用力。 研究对象:物体受力运动
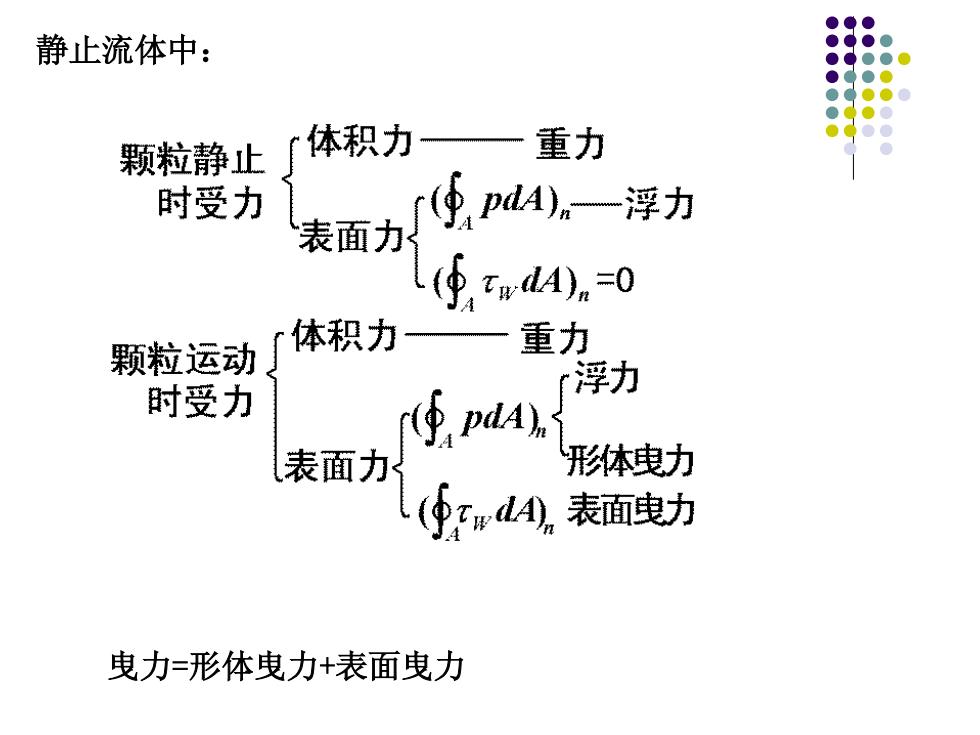
静止流体中: 颗粒静止 「体积力 重力 时受力 表面力 ⑤p4。浮力 (④#dA)n=0 颗粒运动 体积力 重力 时受力 浮力 pdA) 表面力 形体曳力 (小?#dA,表面曳力 曳力=形体曳力+表面曳力
曳力=形体曳力+表面曳力 静止流体中:

5.2.2静止流体中 粒的自由降 (1)沉降速度u—球形颗粒的自由沉降 方F 静止流体中,固体受力: 重g mg 三d,Y (5-9) 6 相速度u 浮力F m yg d,3g(5-11) 6 运动时:浮力、重力和曳力(表面曳 粒在流体中流 所受阻 力和形体曳力),而曳力随着颗粒与流体间的相对运动速度而 变,可仿照流体流动阻力的计算式写为 F。]A, Yu2 球形粒A d 2 4 (5-13) Yu2 Fp 2
曳力 FD �粒在流体中流��所受阻力 相 速度u 重力Fg mg d p p g 3 6 浮力 g d g m F p p b 3 6 运动时:浮力、重力和曳力(表面曳 力和形体曳力),而曳力随着颗粒与流体间的相对运动速度而 变,可仿照流体流动阻力的计算式写为 2 2 u FD Ap 2 4 A d 球形 粒 4 2 2 2 u FD d p 静止流体中,固体受力: 5.2.2 静止流体中�粒的自由�降 (1)沉降速度ut ——球形颗粒的自由沉降 (5-9) (5-11) (5-13)

Fs Fo Fp ma (5-14) dyg君s1,d a 颗粒开始沉降的瞬间,速度=0,因此曳力F=0,amax 颗粒开始沉降后,u↑→FD个;u→4,a=0。 等速阶段中颗粒相对与流体的运动速度,称自由 降速度。 当a=0旺adg 6 护度西 4dng(Y。) 3Y] 一自由 降速度表式 (5-17/18)
d a u d p p g d g d p p p 3 2 3 3 2 6 6 4 2 6 (a) 颗粒开始沉降的瞬间,速度u=0,因此曳力FD=0,a→max 颗粒开始沉降后,u ↑ →FD ↑;u →ut ,a=0 。 等速阶段中颗粒相对与流体的运动速度ut 称 自由 降速度。 当a=0时,u=ut,代入(a)式 0 6 6 4 2 2 3 3 2 t s p u d p g d g d p 3 4 ( ) p p t d g u ——自由 降速度表 式 F F F ma g b D ( ) p t d u (5-17/18) (5-14)

d Yu (2)曳力系数4P144) 888 通过因次分析法得知,ζ值是颗粒与流体相对运动时 的雷诺数Rep的函数。 对于球形颗粒的曲线,按Re值大致分为三个区: ①层流区或斯托克斯kes)定律区(得 Yg u, 18Π 斯托克斯公式 (5-19) 影响因素:dp,△gg,4 思考:.气固分离,气体先加热后沉降还是先沉降后加热?
(2)曳力系数ζ(P144) 通过因次分析法得知,ζ值是颗粒与流体相对运动时 的雷诺数Rep的函数。 对于球形颗粒的曲线,按Rep值大致分为三个区: ①层流区或斯托克斯(stokes)定律区(Rep<2) Re p 24 18 2 d g u p p t ——斯托克斯公式 影响因素:dp,Δρ,g,μ 思考:.气固分离,气体先加热后沉降还是先沉降后加热? ( ) p t d u (5-6) (5-19)