
(3)实际沉降影响沉降速度的因素 ①颗粒的体积浓度 在前面介绍的各种沉降速度关系式中,当颗粒的体积浓 度小于0.2%时,理论计算值的偏差在1%以内,但当颗粒浓 度较高时,由于颗粒间相互作用明显,便发生干扰沉降, 自由沉降的公式不再适用。 ②端效应 u, 当器壁尺寸远远大于颗粒尺寸时,{ 例如在109拟上) 2.1 鑫爱短动忽略,否则需加以考虑。 D≠ d太小(《0.5μm),与分子自由程可比,自由沉降公式不 工口口
(3)实际沉降影响沉降速度的因素 ①颗粒的体积浓度 在前面介绍的各种沉降速度关系式中,当颗粒的体积浓 度小于0.2%时,理论计算值的偏差在1%以内,但当颗粒浓 度较高时,由于颗粒间相互作用明显,便发生干扰沉降, 自由沉降的公式不再适用。 ② 端效应 当器壁尺寸远远大于颗粒尺寸时,(例如在100倍以上) 容器效应可忽略,否则需加以考虑。 D d u u t t 1 2.1 ' ③分子运动 dp太小(<0.5μm),与分子自由程可比,自由沉降公式不 再适用
④颗粒形状的影响 对于非球形颗粒,雷诺准数Re,中的直径要用当量直径de代替, d2(Y,Y)g 18Π 颗粒的球形度愈小,对应于同一R值的阻力系数愈大但值对 的影响在层流区并不显著, 随着Rep的增大,这种影响变大。 ⑤液滴或气泡 液滴直径山 变形、内部环流、破碎 刚球液滴 环流液滴摆动液滴
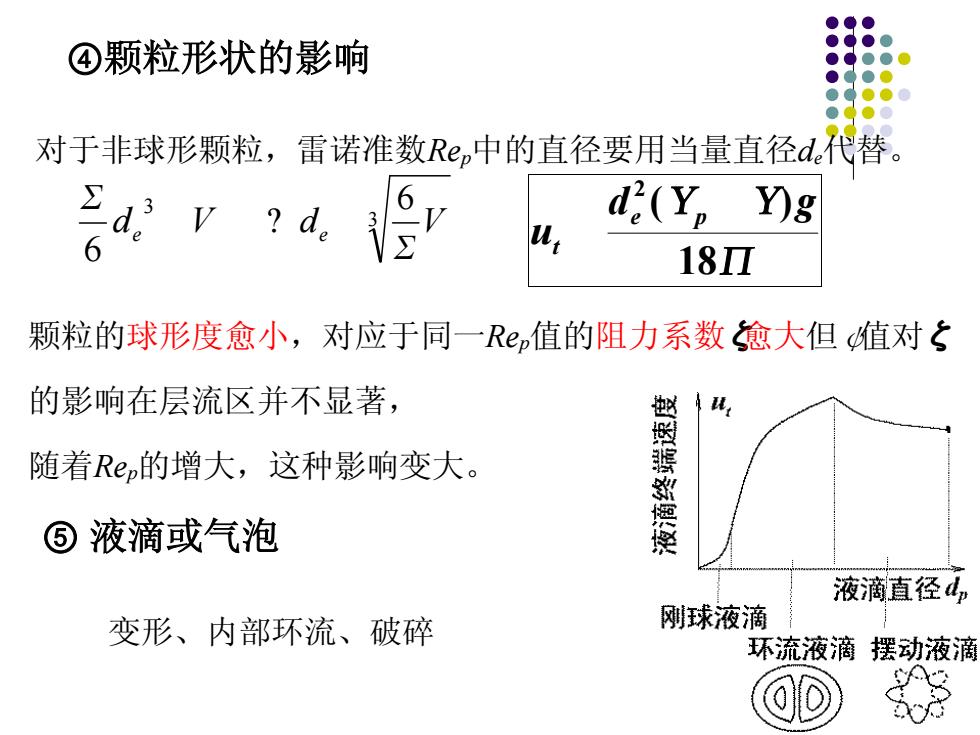
④颗粒形状的影响 对于非球形颗粒,雷诺准数Rep中的直径要用当量直径de代替。 de V 3 6 3 6 de V 颗粒的球形度愈小,对应于同一Rep值的阻力系数ζ愈大但ψ值对ζ 的影响在层流区并不显著, 随着Rep的增大,这种影响变大。 18 ( ) 2 d g u e p t ⑤ 液滴或气泡 变形、内部环流、破碎
(4)氵 沉降计篁 4dg(YY) 公式: 3Y] I dpu,Y 分三段区域表达, I 为判据 变量:dpu,4A,9共6个,待求变量为dp,之一,都在判据 中 a,2y。Y u, Rep dou,Y n 假设沉降属于层流区 18Π→ Rep 所求4Rep<2 公式适 判断 艾 公式 用止 求 Re>2
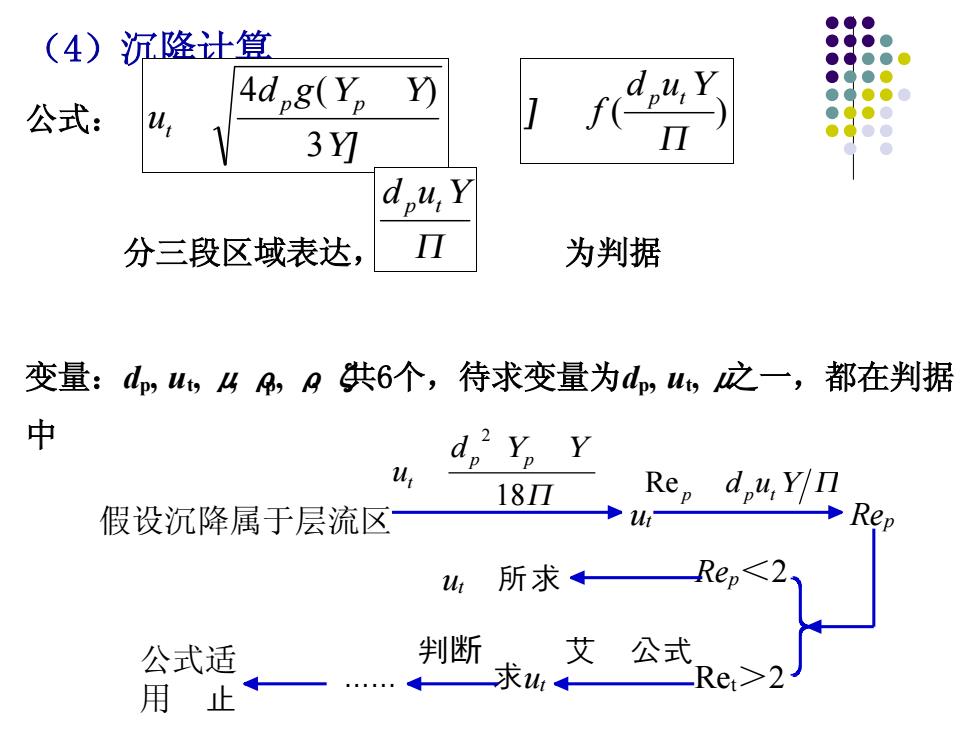
(4)沉降计算 公式: 分三段区域表达, 为判据 变量:dp, ut, μ, ρp, ρ, ζ共6个,待求变量为dp, ut, μ之一,都在判据 中 3 4 ( ) p p t d g u ( ) d put f d put 假设沉降属于层流区 18 2 p p t d u ut Re p d put Rep Rep<2 ut 所求 Ret>2 艾 公式 求ut 判断 . 公式适 用 止
改进判据: Re d,u,Y 4d(Y。Y)g 由 I 3Y2 恰当组合,消去待求变量 组成新判据 尕e2可消去w 尔e可消去, 例2斯托为 24判据值 Re Re<2,由 得512
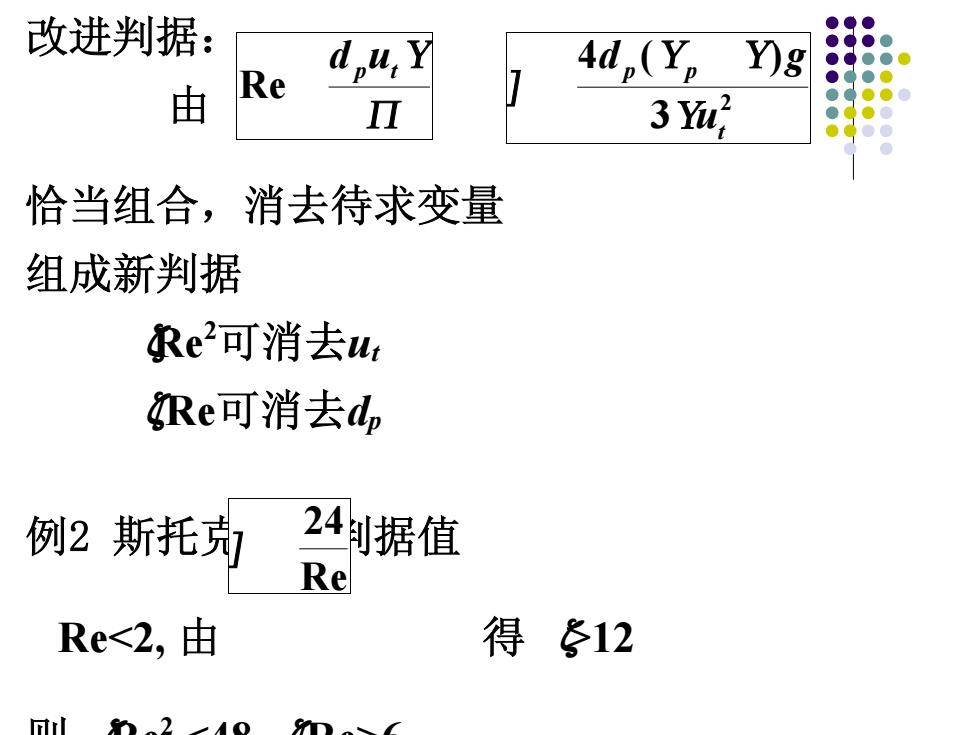
改进判据: 由 和 恰当组合,消去待求变量 组成新判据 ζRe2 可消去ut ζ/Re可消去dp 例2 斯托克斯区判据值 Re<2, 由 得 ζ>12 则 ζRe2 <48, ζ/Re>6 d put Re 2 3 4 ( ) t p p u d g Re 24

摩擦数群法 Y 由 4gdY, Y得 Adpg Yp 3]Y 3h,2 Re2 4dYY Yg ORe,2 ㎡ 3㎡ 因是Re的已知函数, ⑧er必然也是Re的已知函数, g~Re,曲线便可转化成Re~Re,曲线。 计算u时,先由已知数据算出你e的值,再由Re2Re曲 线查得Re,值,最后由Re,他,。 u, d,Y
2 2 2 2 2 Re p t t d u Θ 2 3 2 3 4 Re d p g t p 因ζ是Ret的已知函数,ζRet 2 必然也是Ret的已知函数, ζ~Ret曲线便可转化成 ζRet 2 ~Ret曲线。 计算ut时,先由已知数据算出ζRet 2 的值,再由ζRet 2~ Ret曲 线查得Ret值,最后由Ret反算ut 。 p t t d u Re 摩擦数群法 3 4 p p t gd 由 u 得 2 3 4 t p p u d g