
定义 从K最近邻算法的角度来看,就是让目标样 本与其他正样本距离更近、与其他负样本距离 更远,从而使得其近邻中的正样本比例更高, 更大概率被判断成正样本
定义 从K最近邻算法的角度来看,就是让目标样 本与其他正样本距离更近、与其他负样本距离 更远,从而使得其近邻中的正样本比例更高, 更大概率被判断成正样本
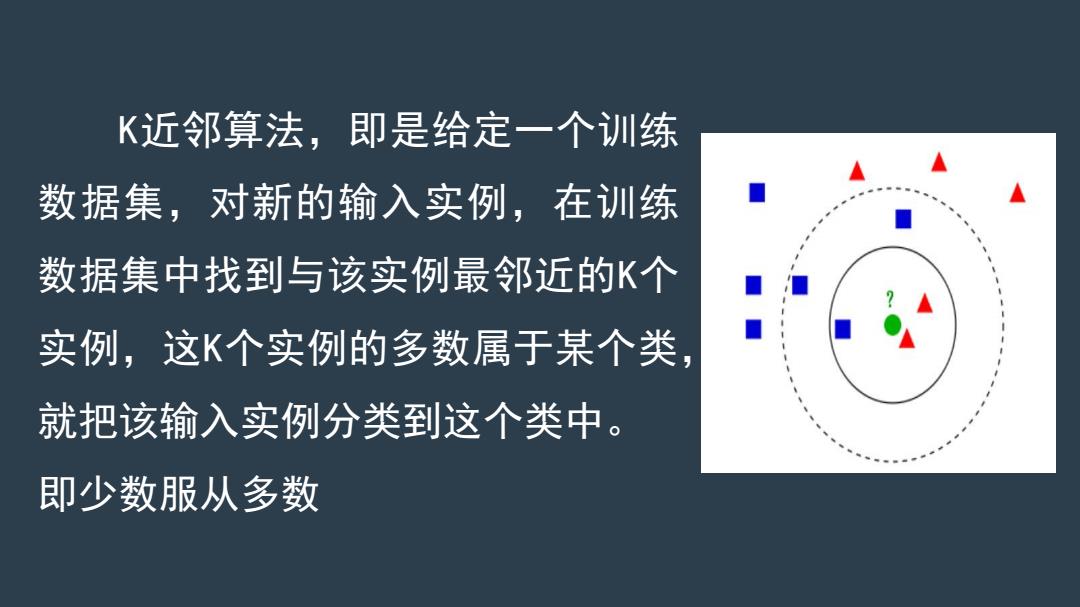
K近邻算法,即是给定一个训练 数据集,对新的输入实例,在训练 数据集中找到与该实例最邻近的K个 实例,这K个实例的多数属于某个类, 就把该输入实例分类到这个类中。 即少数服从多数
K近邻算法,即是给定一个训练 数据集,对新的输入实例,在训练 数据集中找到与该实例最邻近的K个 实例,这K个实例的多数属于某个类, 就把该输入实例分类到这个类中。 即少数服从多数
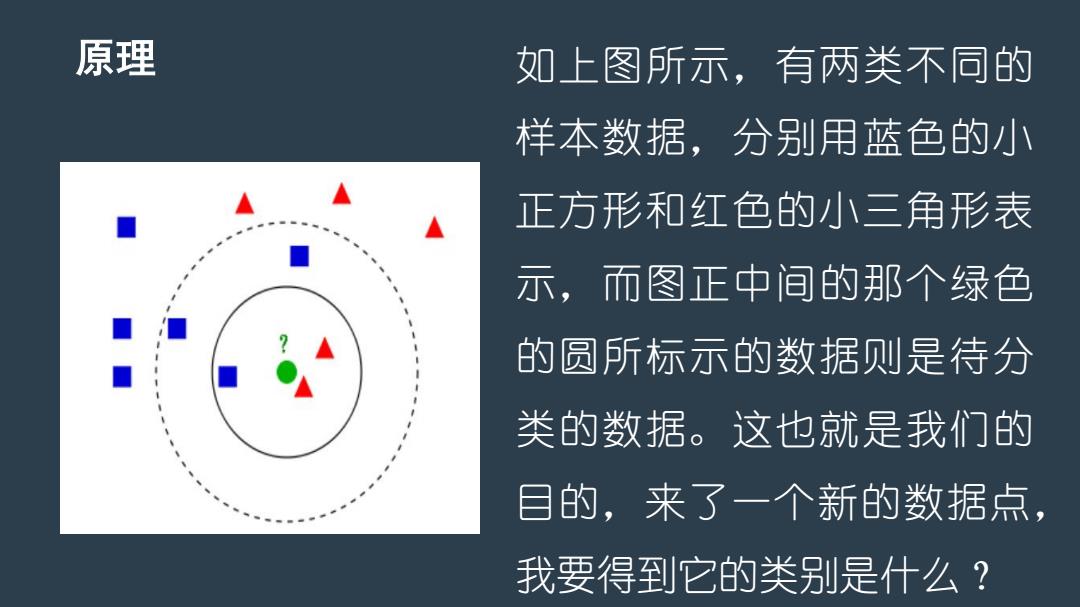
原理 如上图所示,有两类不同的 样本数据,分别用蓝色的小 正方形和红色的小三角形表 示,而图正中间的那个绿色 的圆所标示的数据则是待分 类的数据。这也就是我们的 目的,来了一个新的数据点, 我要得到它的类别是什么?
原理 如上图所示,有两类不同的 样本数据,分别用蓝色的小 正方形和红色的小三角形表 示,而图正中间的那个绿色 的圆所标示的数据则是待分 类的数据。这也就是我们的 目的,来了一个新的数据点, 我要得到它的类别是什么?
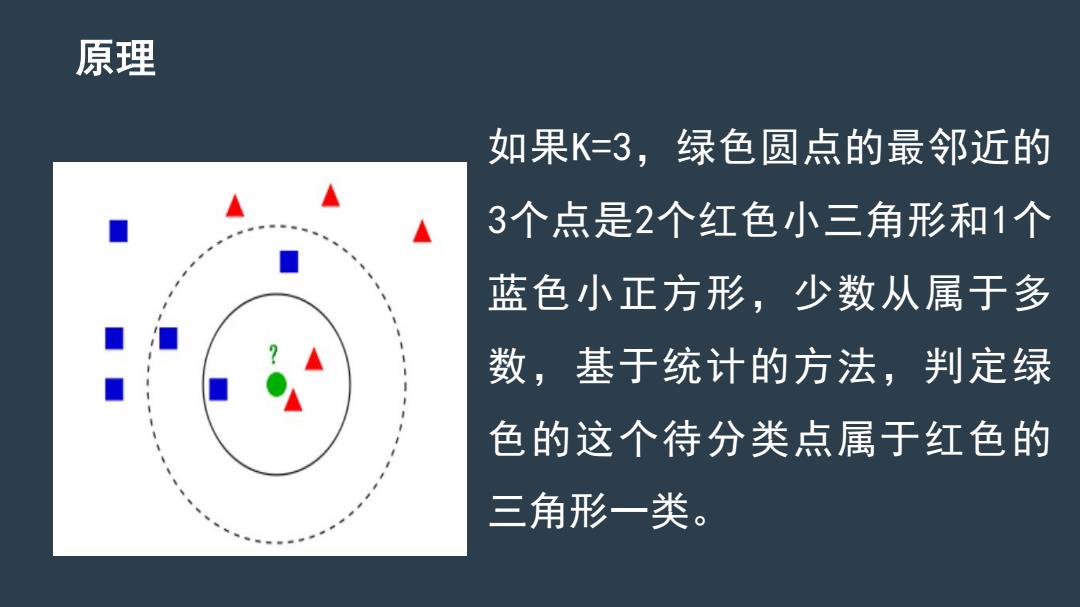
原理 如果K=3,绿色圆点的最邻近的 3个点是2个红色小三角形和1个 蓝色小正方形,少数从属于多 数,基于统计的方法,判定绿 色的这个待分类点属于红色的 三角形一类
原理 如果K=3,绿色圆点的最邻近的 3个点是2个红色小三角形和1个 蓝色小正方形,少数从属于多 数,基于统计的方法,判定绿 色的这个待分类点属于红色的 三角形一类
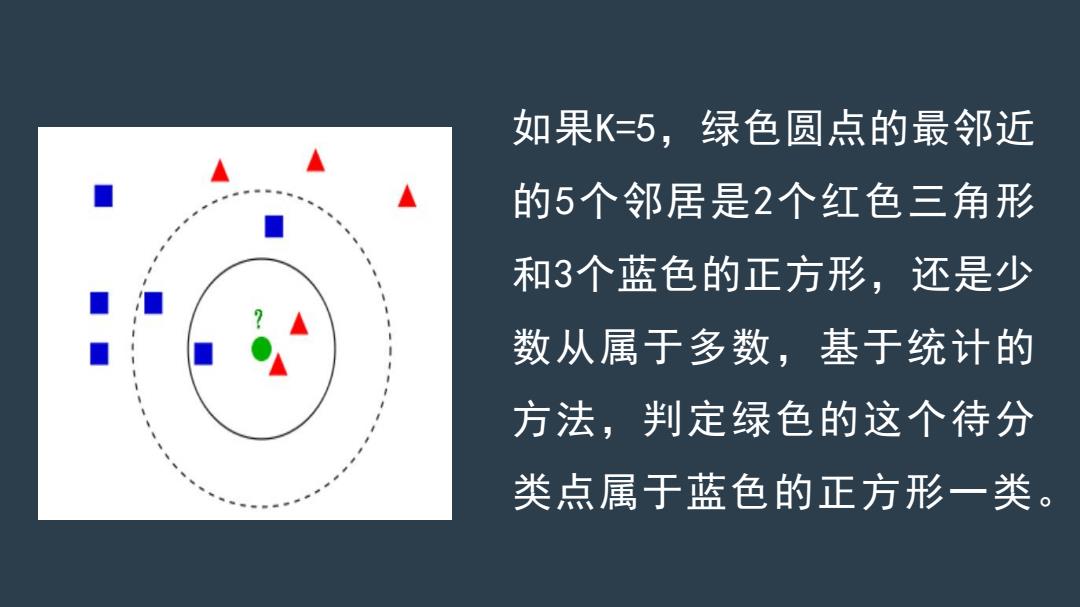
如果K=5,绿色圆点的最邻近 的5个邻居是2个红色三角形 和3个蓝色的正方形,还是少 数从属于多数,基于统计的 方法,判定绿色的这个待分 类点属于蓝色的正方形一类
如果K=5,绿色圆点的最邻近 的5个邻居是2个红色三角形 和3个蓝色的正方形,还是少 数从属于多数,基于统计的 方法,判定绿色的这个待分 类点属于蓝色的正方形一类