
■分析U(r)和总电势UU(r)的关系。设dW为一 球体元,由第1.7节例1.11的结果(P28),取 R1=0,R2=a。可求得电荷密度为Pe、半径为 a的均匀带电球体在球内产生的电势为: ra) U'= 它在球心处取极大值U”=Pa2/2so,故当a→0 时有Um→0即U'→0。于是,U(r)≈U(r) w-fp.ty(wv. (3.2.2)
■ 分析U1(r)和总电势U(r)的关系。设dV 为一 球体元,由第1.7节例1.11的结果(P28),取 R1 = 0,R2 = a。可求得电荷密度为 、半径为 a的均匀带电球体在球内产生的电势为: e 2 2 0 3 , 6 e U a r 它在球心处取极大值 ,故当 时有 即 。于是, U1(r) ≈ U(r) 2 0 / 2 U m e a a0 0 Um U 0 1 ( ) ( ) . 2 e e V W U dV r r (3.2.2)

2.对面电荷分布的情形,设面电荷密度 为σ(r)。类似,将面电荷无限分割为圆状面电 荷元o()dS,它在自身产生的电势不会大丁 0a/28 (a为面元半径,见P26的第1.7节例 1.10),该电势随dS→0(a→0)而趋于零。 于是,U(r)≈U(r),其静电能为: W.--SSo.(rU(rds (3.2.3) S
2. 对面电荷分布的情形,设面电荷密度 为 。类似,将面电荷无限分割为圆状面电 荷元 ,它在自身产生的电势不会大于 (a为面元半径,见P26的第1.7节例 1.10),该电势随 ( )而趋于零。 于是 ,U1(r) ≈ U(r) ,其静电能为: ( ) e r ( ) e r dS dS 0 a0 0 / 2 e a S We e ( )U( )dS 2 1 r r (3.2.3)

3.线电苻分布的情况,不能将静电能写为: 或所-j2,0aw 因为2。(l)d1在自身所在处产生的电势不仅不 趋于零,而且会按lnr (r为离线元d的垂直距 离)趋于无穷。进一步,可证U()也会趋于无穷 大。 这在物理上意味着:要把电荷从极端分散状态压 缩到一条几何线上,外界需要作无穷大的功。这 显然是办不到的。因此,在计算静电能时,无论 线径怎样小的带电体均不能当作线电荷处理
3. 线电荷分布的情况,不能将静电能写为: 1 ( ) ( ) 2 e e L W l U l dl 或 1 1 ( ) ( ) 2 e e L W l U l dl 因为 在自身所在处产生的电势不仅不 趋于零,而且会按 (r为离线元dl的垂直距 离)趋于无穷。进一步,可证U1(l)也会趋于无穷 大。 这在物理上意味着:要把电荷从极端分散状态压 缩到一条几何线上,外界需要作无穷大的功。这 显然是办不到的。因此,在计算静电能时,无论 线径怎样小的带电体均不能当作线电荷处理。 ( ) e l d l ln r

4.多个带电体组成的象统的静电能。设有 N个带电体,体积分别为,2..,VN。可将空 间的总电势U()分为两部分(请思考!为什麽?) U(r)=U,(r)+U(r), ◆式中()表示除第个带电体外其余所有带电 体在r处产生的电势,(r)则表示第i个带电 体在r处产生的电势。按照前述结论,可得: =号ΣS2.(rXdv=)∑叮p,uu+Ur W 2 2 ∑2Jj∬p.ariw+∑2Jj川Pp.,rd
4. 多个带电体组成的系统的静电能。设有 N个带电体,体积分别为V1,V2…,VN。可将空 间的总电势U(r)分为两部分(请思考!为什麽?) ( ) ( ) ( ) ( ), i U r Ui r U r u式中Ui(r)表示除第i个带电体外其余所有带电 体在 r 处产生的电势, 则表示第i个带电 体在 r 处产生的电势。按照前述结论,可得: ( ) ( ) i U r ( ) ( ) , 2 1 ( ) ( ) 2 1 1 1 ( ) N i V e i N i V i e i i r U r dV r U r dV
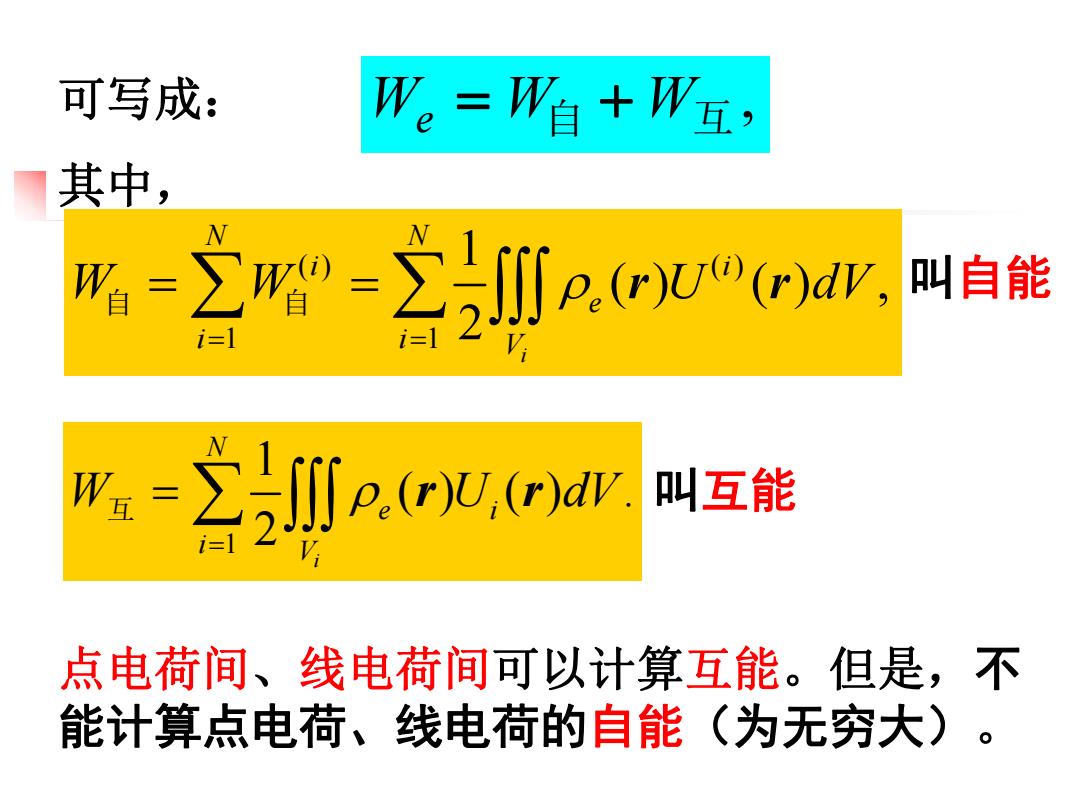
可写成: We=W自+W互, 其中, 形=∑=∑p.(rW(r)a,叫自能 i=1 形z=∑川p,(c)a叫互能 点电荷间、线电荷间可以计算互能。但是,不 能计算点电荷、线电荷的自能(为无穷大)
W W自 W互, 可写成: e 其中, ( ) ( ) 1 1 1 ( ) ( ) , 2 i N N i i e i i V W W U dV 自 自 r r 1 1 ( ) ( ) . 2 i N e i i V W U dV 互 r r 叫自能 叫互能 点电荷间、线电荷间可以计算互能。但是,不 能计算点电荷、线电荷的自能(为无穷大)