
Fibonacci:F=F+Fn2 间题6: 如果要你计算第n个 Fibonacci数,你用递归还是 用循环,还是随便?为什么?
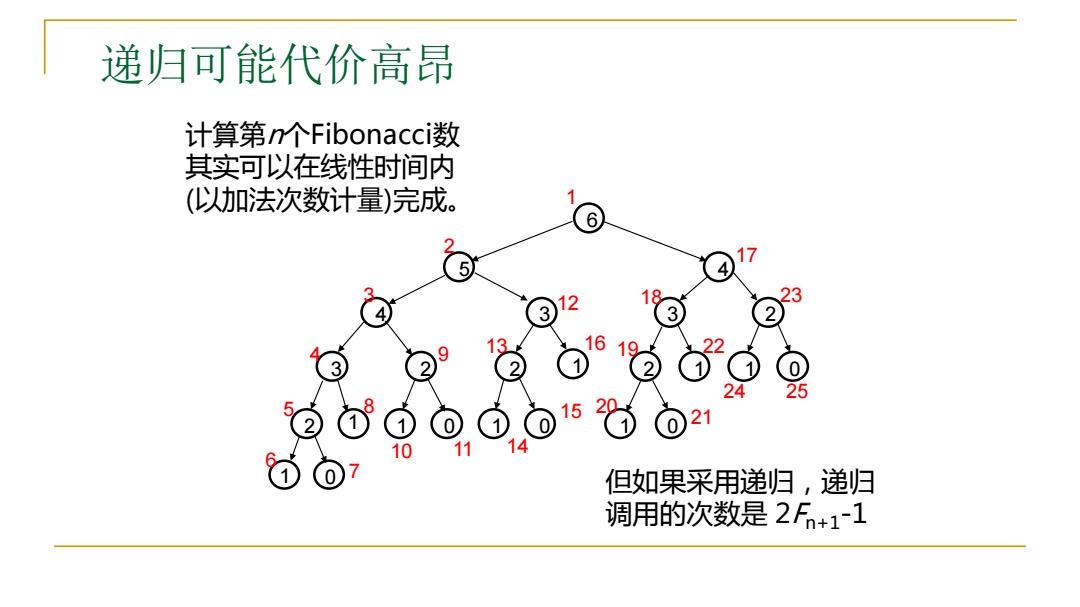
递归可能代价高昂 计算第n个Fibonacci数 其实可以在线性时间内 (以加法次数计量)完成。 6 5 4 2 18 23 3 3 16 9 13 9 2 25 但如果采用递归,递归 调用的次数是2Fn+1~1
递归可能代价高昂 0 0 0 0 0 1 1 1 1 1 1 1 1 2 2 2 2 2 4 3 3 3 6 5 4 13 16 10 11 9 8 12 3 4 5 6 7 14 15 21 2 1 19 18 17 25 23 24 22 20 计算第n个Fibonacci数 其实可以在线性时间内 (以加法次数计量)完成。 但如果采用递归,递归 调用的次数是 2Fn+1-1

问题6.1: 我们有什台办法来应对这种 情况? f1=1;f2=1; 输出f1,f2; for(i=3;i<n,i++) 你有启发吗? f3=f1+f2; 输出f3: f1=f2:f2=f3:
f1=1;f2=1; 输出f1,f2; for(i=3;i<n,i++){ f3=f1+f2; 输出f3; f1=f2;f2=f3; } 你有启发吗?
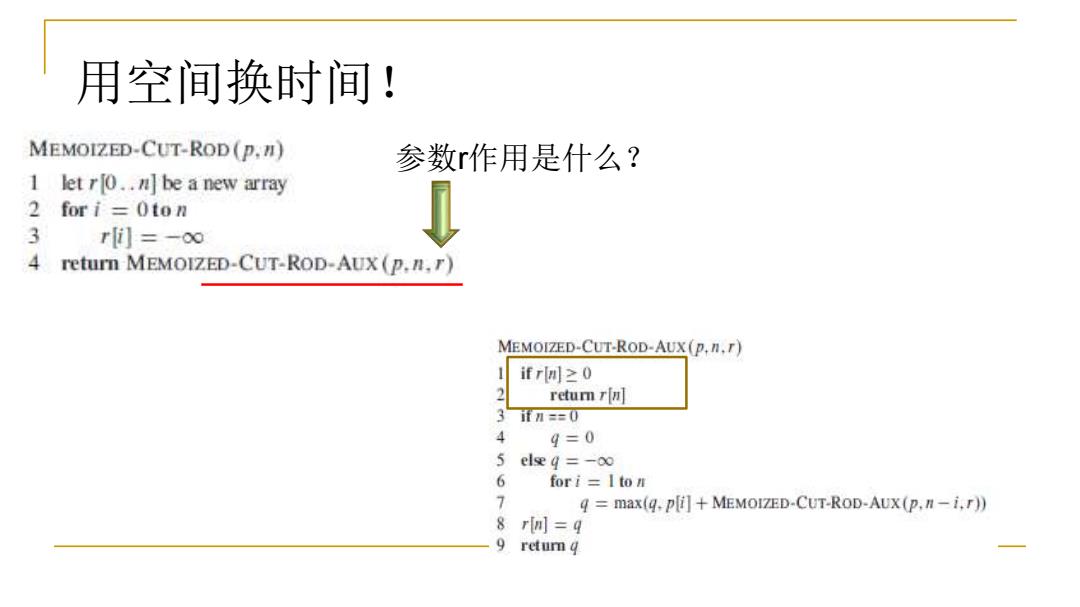
用空间换时间! MEMOIZED-CUT-ROD (p.) 参数r作用是什么? 1etrO.月be a new array 2 for i Oton 3 rli]=-oo 4 return MEMOIZED-CUT-ROD-AUX(p.n.r) MEMOIZED-CUT-ROD-AUX (p.n.) ifr间≥0 2 retur rn] 3f刀==0 4 9=0 5eleg=-o∞ 6 fori I to n 7 q max(q.p[i]MEMOIZED-CUT-ROD-AUX(p,n-i,r)) 8 rin]=q 9 retum q
参数r作用是什么? 用空间换时间!
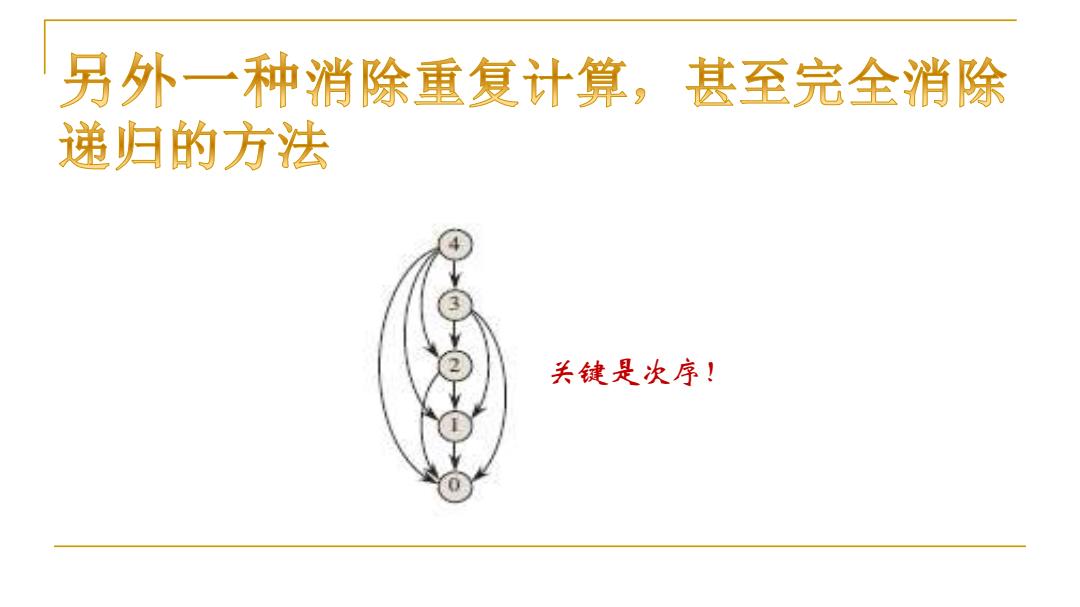
另外一种消除重复计算,甚至完全消除 递归的方法 关键是次序!
关键是次序!