
计算机问题求解-论题1-3 常用证明方法及其逻辑正确性 陶先平 2021年10月21日
计算机问题求解-论题1-3 常用证明方法及其逻辑正确性 陶先平 2021年10月21日

Outlines ·反证法及其逻辑正确性 ·分情形证明法及其逻辑正确性 ·数学归纳法及其逻辑正确性 ·鸽笼原理证明法及其逻辑正确性
Outlines • 反证法及其逻辑正确性 • 分情形证明法及其逻辑正确性 • 数学归纳法及其逻辑正确性 • 鸽笼原理证明法及其逻辑正确性

V2 is not rational (Pythagoreans)? Proof. Suppose,to the contrary,that v2 is rational.Then there exist inte- gers p and q(with q nonzero)such that v2=p/q.We may assume that p and q have no common factor,for if they did,we would sim- plify and begin again.Now,we have that v2q p.Squaring both sides,we obtain 2g2 =p2.Thus p2 is e s even, we know from Problem 3.1 that p m 你有没有怀疑过 2m for some integer m.This means t 这个"therefore” see that g2 =2m2.But this means that a 的正确性? m Prob- lem 3.1 that g is even.So p and 2,which is completely absurd,since we assumed ne o common factor. Therefore our assumption that v2 is rational must be wrong and we have completed the proof of the theorem. ■
2 is not rational (Pythagoreans)? 你有没有怀疑过 这个”therefore” 的正确性?

There are infinitely many prime numbers. Proof. We set a contrary of To prove this statement suppose,to the contrary,that there are our theorem and use finitely many primes.Then we may write these finitely many this assumption to primes in ascending order as start 2,3,5,,N, where N is the largest prime.Now consider the number M defined by Then we get a M=(2·3.5·…·N+1 contradiction through If M is prime,then M is a prime that is larger than the largest prime a valid argument N.Therefore,we must conclude that M is not prime,and so it is divisible by some prime number,P.However,P must appear inthe list of primes 2,3,5, which we gave earlier.Bu when we divide M by P,we obtain a Then we get the remainder of1 Therefore,P cannot be a factor of M and we have theorem quickly contradicted our assumption tha there are finitely many primes. Thus,tere cxist infinitely many primes. ■
There are infinitely many prime numbers. We set a contrary of our theorem and use this assumption to start Then we get a contradiction through a valid argument Then we get the theorem quickly
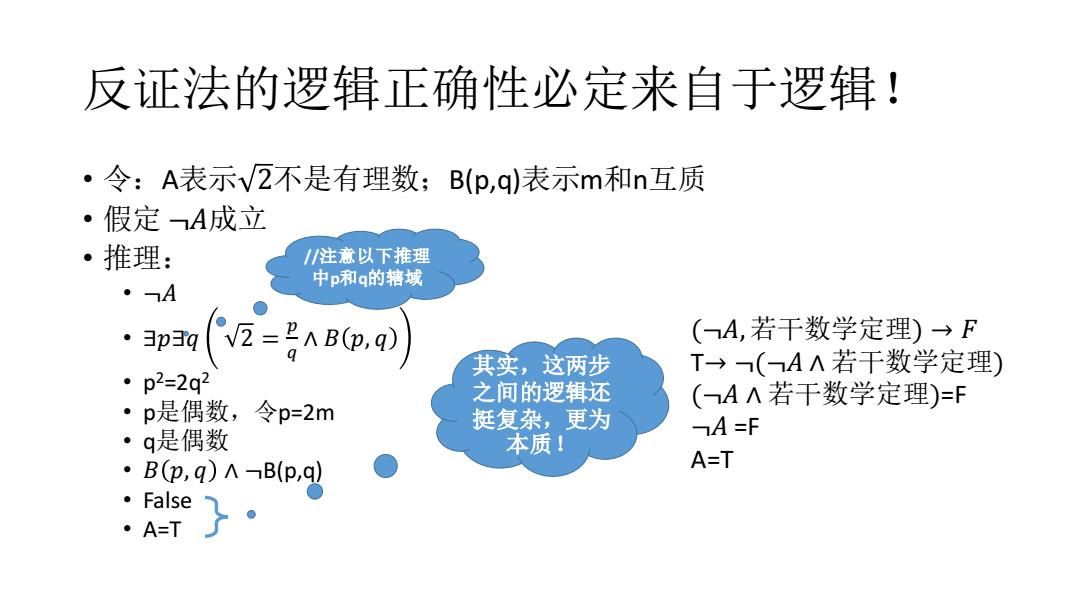
反证法的逻辑正确性必定来自于逻辑! ·令:A表示V2不是有理数;B(p,q)表示m和n互质 ·假定A成立 ·推理: /注意以下推理 中p和g的辖域 ·A ·3p3q V=B(p.Q) (A,若干数学定理)→F 0 其实,这两步 T→(A∧若干数学定理) ·p2=2q2 之间的逻辑还 ·p是偶数, (AA若干数学定理)=F 令p=2m 挺复杂,更为 ·q是偶数 A =F 本质! ·Bp,q)NB(p,qg A=T ·False ·A=T
反证法的逻辑正确性必定来自于逻辑! • 令:A表示 2不是有理数;B(p,q)表示m和n互质 • 假定 ¬𝐴成立 • 推理: • ¬𝐴 • ∃𝑝∃𝑞 2 = 𝑝 𝑞 ∧ 𝐵 𝑝, 𝑞 • p 2=2q2 • p是偶数,令p=2m • q是偶数 • 𝐵 𝑝, 𝑞 ∧ ¬B(p,q) • False • A=T (¬𝐴, 若干数学定理) → 𝐹 T→ ¬(¬𝐴 ∧ 若干数学定理) (¬𝐴 ∧ 若干数学定理)=F ¬𝐴 =F A=T //注意以下推理 中p和q的辖域 其实,这两步 之间的逻辑还 挺复杂,更为 本质!