
计算机问题求解-论题3-12 图中的匹配与因子分解 2020-12-2
计算机问题求解---论题3-12 图中的匹配与因子分解 2020-12-2
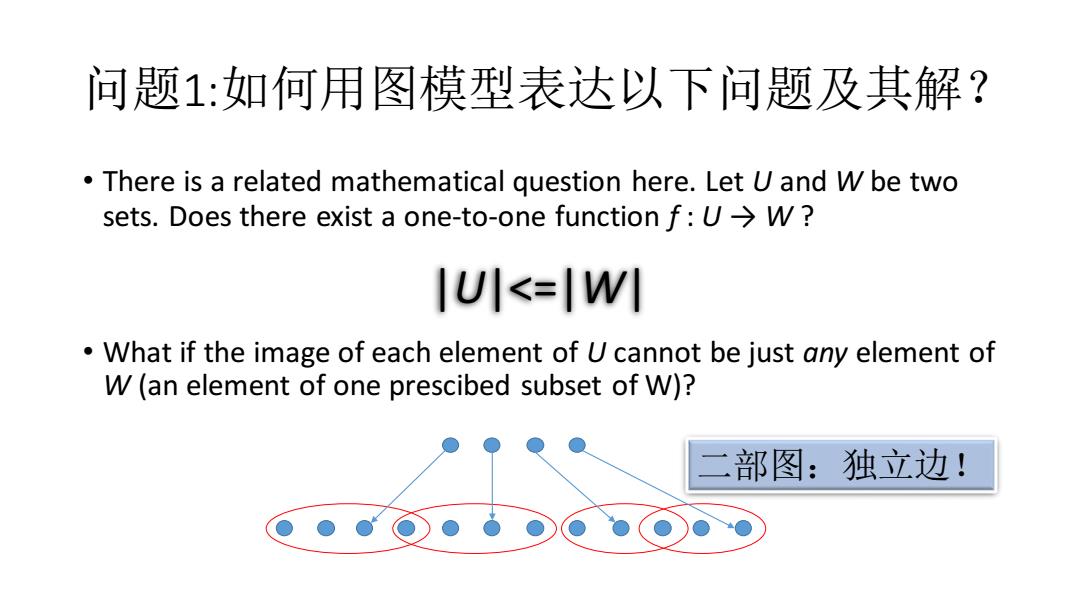
问题1:如何用图模型表达以下问题及其解? There is a related mathematical question here.Let U and W be two sets.Does there exist a one-to-one function f:U>W? lU<=|W What if the image of each element of U cannot be just any element of W(an element of one prescibed subset of W)? 二部图:独立边!
问题1:如何用图模型表达以下问题及其解? • There is a related mathematical question here. Let U and W be two sets. Does there exist a one-to-one function f : U → W ? • What if the image of each element of U cannot be just any element of W (an element of one prescibed subset of W)? |U|<=|W| 二部图:独立边!
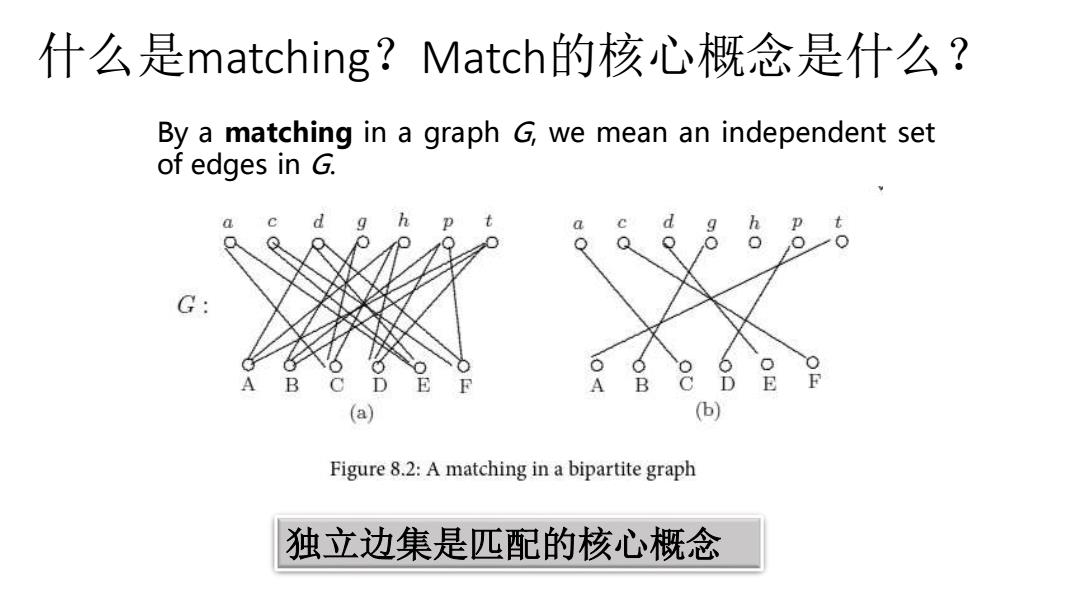
什么是matching?Match的核心概念是什么? By a matching in a graph G,we mean an independent set of edges in G. a d h A B 品 (a) (b) Figure 8.2:A matching in a bipartite graph 独立边集是匹配的核心概念
什么是matching?Match的核心概念是什么? 独立边集是匹配的核心概念 By a matching in a graph G, we mean an independent set of edges in G
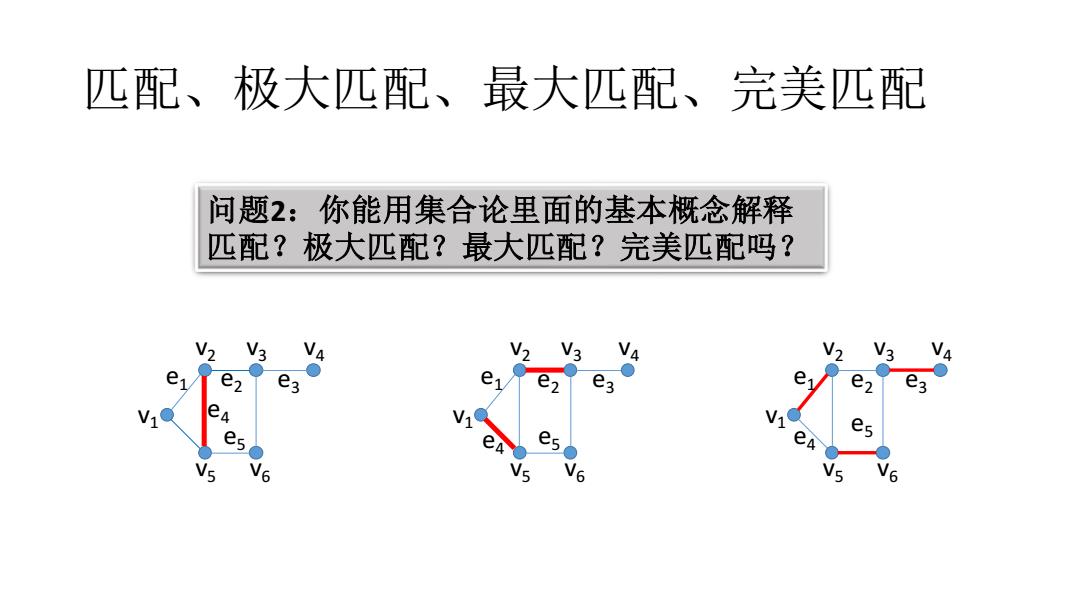
匹配、极大匹配、最大匹配、完美匹配 问题2:你能用集合论里面的基本概念解释 匹配?极大匹配?最大匹配?完美匹配吗? e e e N es 6 6 6
匹配、极大匹配、最大匹配、完美匹配 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 问题2:你能用集合论里面的基本概念解释 匹配?极大匹配?最大匹配?完美匹配吗?

二部图中最大匹配的存在性 Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. For a nonempty set X of U the neighborhood MX)of X is the union of the neighborhoods Mx).Equivalently,MX)consists of all those vertices of W that are the neighbors of one or more vertices in X.The graph G is said to satisfy Hall's condition if MX) for every nonempty subset Xof U
二部图中最大匹配的存在性 For a nonempty set X of U, the neighborhood N(X) of X is the union of the neighborhoods N(x). Equivalently, N(X) consists of all those vertices of W that are the neighbors of one or more vertices in X. The graph G is said to satisfy Hall’s condition if |N(X)| ≥ |X| for every nonempty subset X of U