
计算机问题求解一论题3-9 All-Pair Shortest Paths 2022年11月9 日
计算机问题求解 – 论题3-9 - All-Pair Shortest Paths 2022年11月9 日
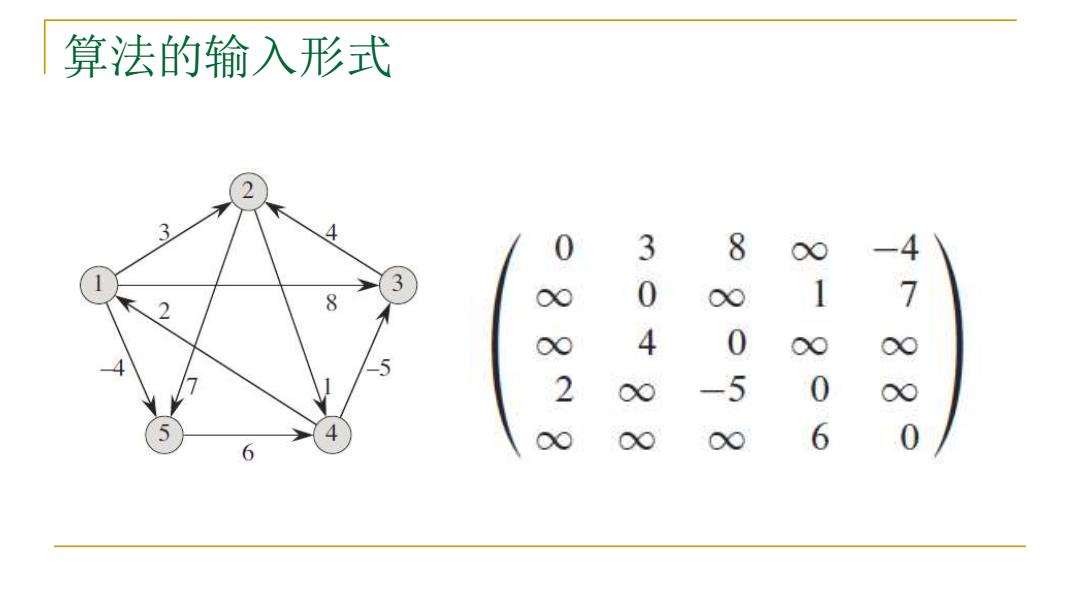
算法的输入形式 2 3 4 0 3 8 00 3 8 0 0∞ 1 > 4 0 5 2 -5 0 5 4 00 00 00 6 0 6
算法的输入形式

最直观的解法 Bellman-Ford算法执行VI次 ■Dijkstra算法执行VI次 口f可能
最直观的解法 ◼ Bellman-Ford算法执行|V|次 ◼ Dijkstra算法执行|V|次 ❑ if可能

最优子结构:对于任意i,j间最短路p,其间的 任意子路径均最短 假设这是从到的最短通路,经过k If vertices i and j are distinct,then we decompose path p into ikj,where path p'now contains at most m-1 edges.By Lemma 24.1, p'is a shortest path from i to k,and sd(i.)=8(i,k+wki 这对我们未来的“递归”有什么启发?
i k j 假设这是从i到j的最短通路,经过k p ’ 最优子结构:对于任意i,j间最短路p,其间的 任意子路径均最短 这对我们未来的“递归”有什么启发?

一种“最优解”的递归定义方式 ■表达节点到的最短路径长度的动态规划递归表达式: 口1,L(i,j)=w 2.L(i,j)=min {L(i,k)+Wkj 1≤k≤n 但参考书上采用了另外一种递归表达方式,有何不同? Now,letbe the minimum weight of any path from vertex ito vertexthat contains at most m edges. When m =0,there is a shortest path from i to j with no edges if and only if i=j.Thus, )ifi=j. fi≠j. =mm(g-”经-”+)
一种“最优解”的递归定义方式 ◼ 表达节点i到j的最短路径长度的动态规划递归表达式: ❑ 1,𝐿(𝑖,𝑗) = 𝑤𝑖𝑗 ❑ 2, 𝐿 𝑖,𝑗 = min 1≤𝑘≤𝑛 {𝐿(𝑖, 𝑘) + 𝑤𝑘𝑗} 但参考书上采用了另外一种递归表达方式,有何不同?