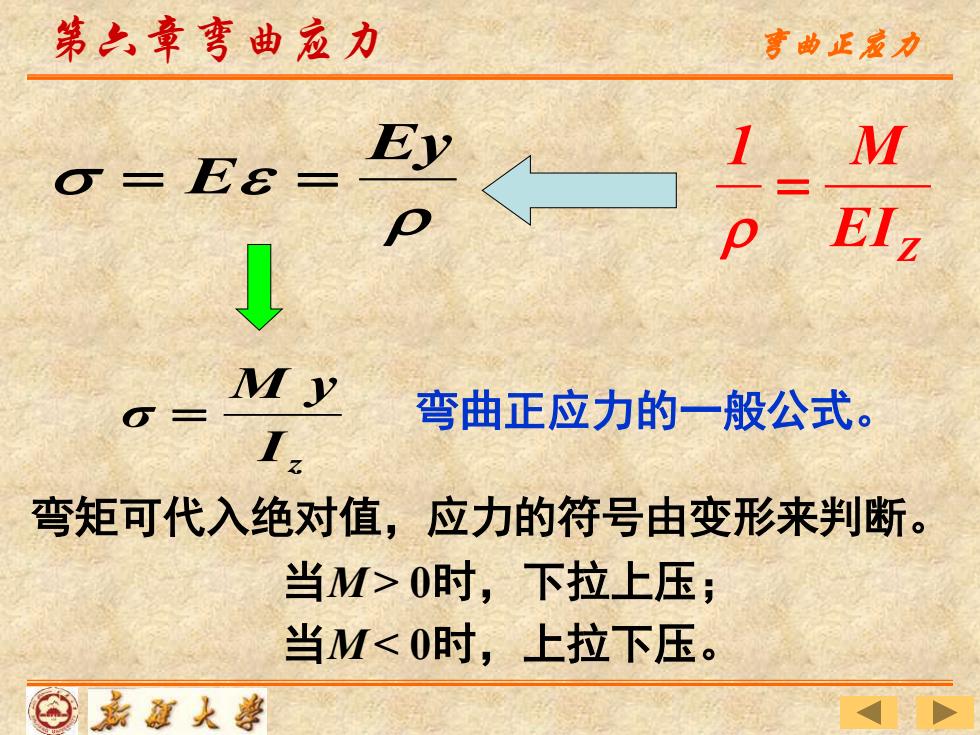
第六章弯曲应力 亨曲正哀力 o-E8- Ey IM My 弯曲正应力的一般公式。 I 弯矩可代入绝对值,应力的符号由变形来判断。 当M>0时,下拉上压; 当M<0时,上拉下压。 ⊙嘉面人婆
z I M y σ = 弯曲正应力的一般公式。 Ey E = = EIZ 1 M = 弯矩可代入绝对值,应力的符号由变形来判断。 当M > 0时,下拉上压; 当M < 0时,上拉下压。 第六章弯曲应力 弯曲正应力
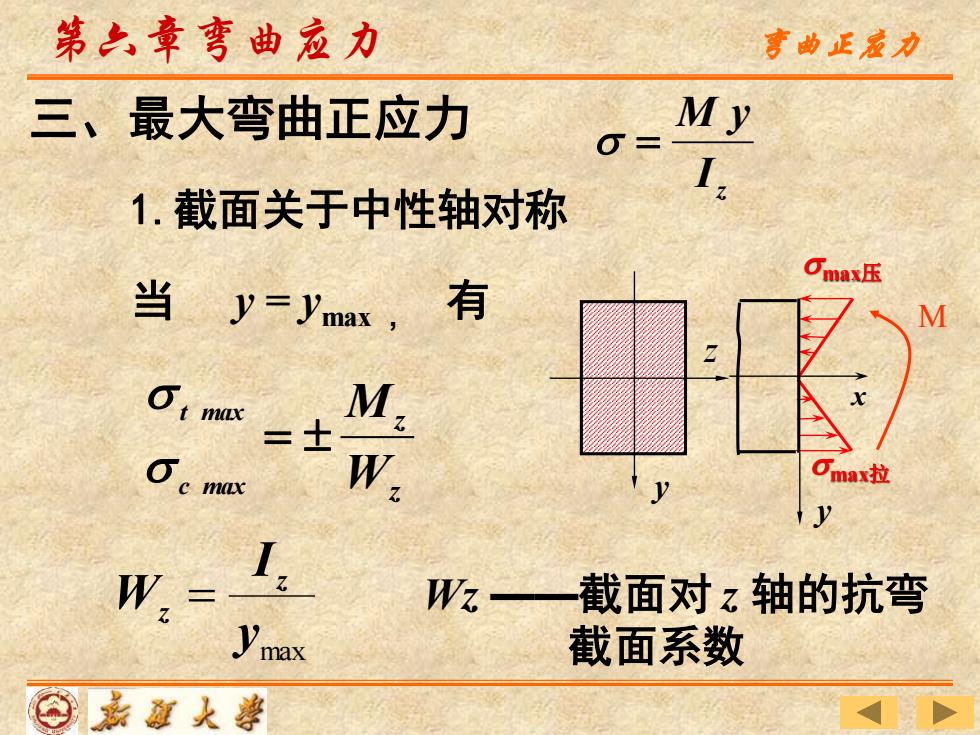
第六章弯曲应力 弯曲正家力 三、最大弯曲正应力 My 0= I. 1.截面关于中性轴对称 当y=ymax,有 Cmax压 二士 M e max W Omax拉 W2= 1 W?一截面对z轴的抗弯 ymax 截面系数 ⊙嘉题人尊
z I M y = z z W M c max t max = max y I W z z = 当 y = ymax , 有 1.截面关于中性轴对称 三、最大弯曲正应力 max压 y x max拉 z y M 第六章弯曲应力 弯曲正应力 Wz ——截面对 z 轴的抗弯 截面系数
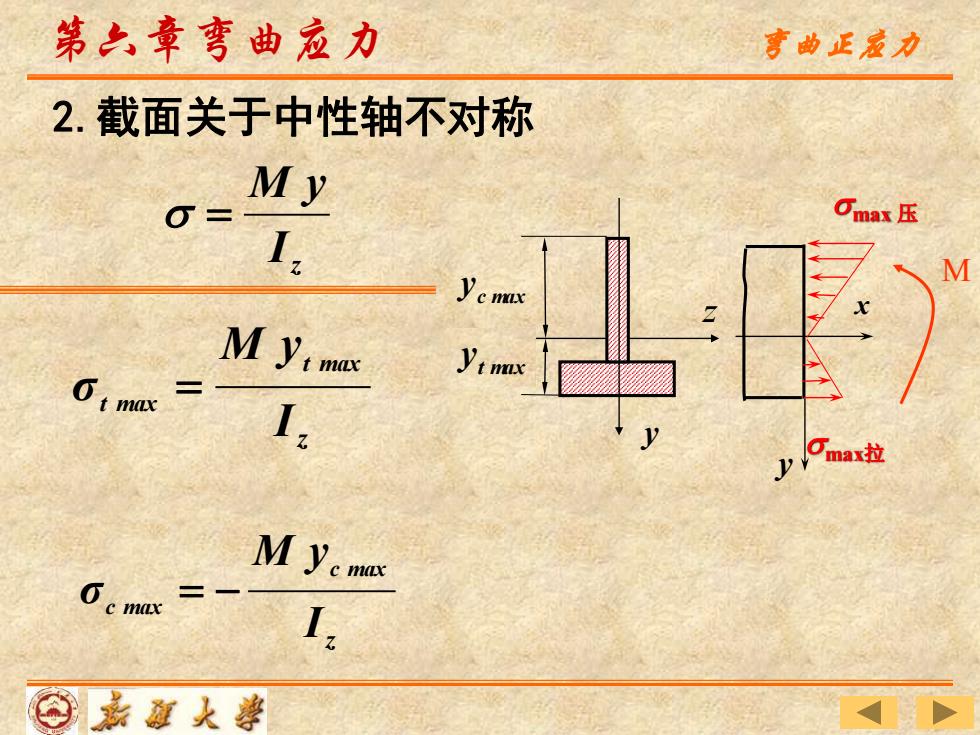
第六章弯曲应力 亨曲正哀力 2.截面关于中性轴不对称 My 可max压 1, M y:mx yimx I y口max拉 M yemas I ⊙嘉道人善
y x z I M y = 2.截面关于中性轴不对称 max 压 max拉 z I M y σ t max t max = z I M y σ c max c max = − z y M 第六章弯曲应力 弯曲正应力 t max y c max y
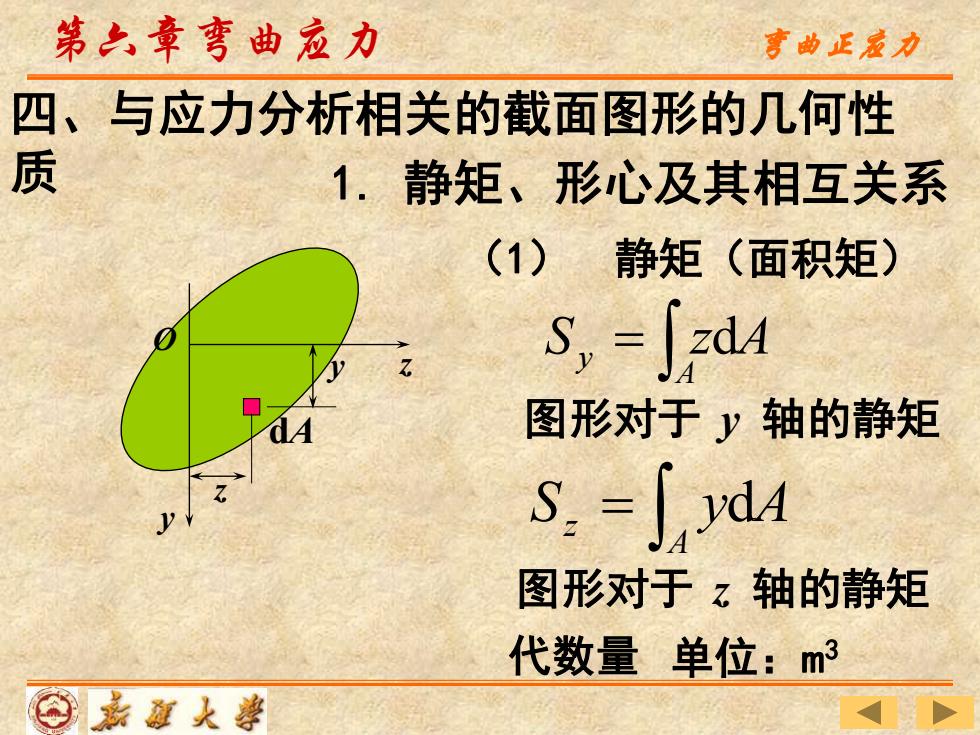
第之章弯曲应力 亨曲正宝力 四、与应力分析相关的截面图形的几何性 质 1.静矩、形心及其相互关系 (1)静矩(面积矩) S,=JadA 图形对于y轴的静矩 S.=d 图形对于z轴的静矩 代数量单位:m3 ⊙嘉瓢大尊
= A Sy zdA z y O dA y z = A Sz ydA 图形对于 y 轴的静矩 图形对于 z 轴的静矩 1. 静矩、形心及其相互关系 (1) 静矩(面积矩) 代数量 单位:m 3 第六章弯曲应力 弯曲正应力 四、与应力分析相关的截面图形的几何性 质
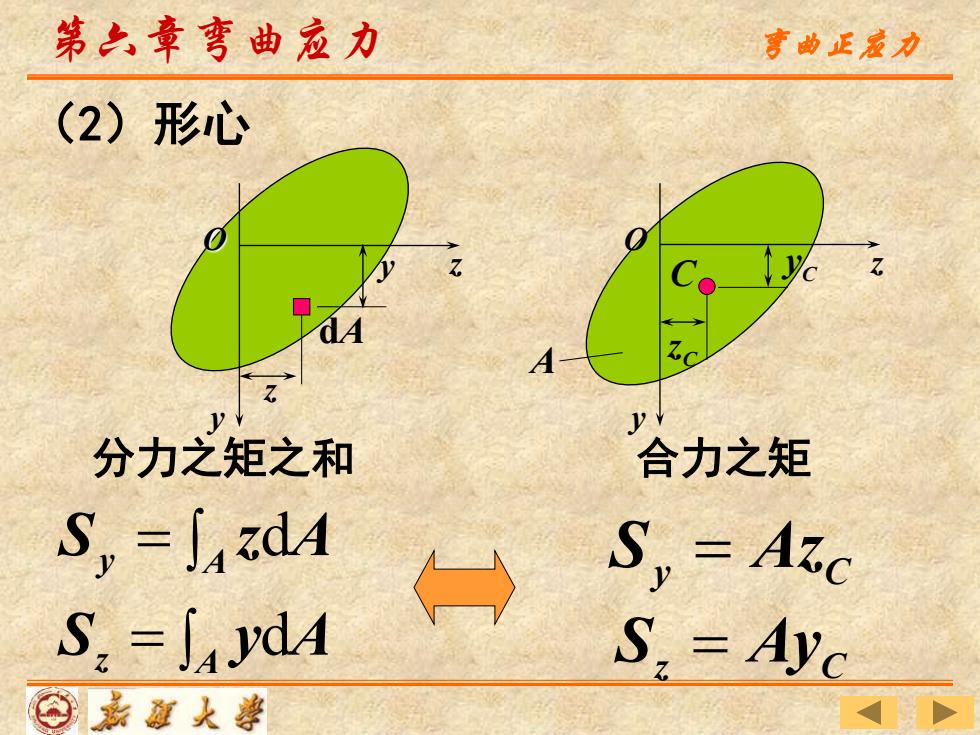
第六章弯曲在力 亨曲正哀力 (2)形心 A V Y 分力之矩之和 合力之矩 S,=∫Ad4 S,=Aic S.=lydA S,=Ayc ⊙嘉道人薯
A Sy = AzC Sy = A zdA Sz = A ydA Sz = AyC 分力之矩之和 合力之矩 (2)形心 z y O dA y z z y O C y C z C 第六章弯曲应力 弯曲正应力