
第七章弯曲变形 百嘉道火事
第七章 弯曲变形

第七章弯曲变形 §7-1引言 §7-2挠曲线近似微分方程 §7-3计算梁位移的积分法 §7-5计算梁位移的叠加法 §7-6简单静不定梁 §7-7梁的刚度条件与合理刚度设计 ⊙嘉面人善
第七章弯曲变形 §7-1 引 言 §7-2 挠曲线近似微分方程 §7-3 计算梁位移的积分法 §7-5 计算梁位移的叠加法 §7-6 简单静不定梁 §7-7 梁的刚度条件与合理刚度设计

第七章弯曲变形 引言 87-1引言0 x q 一、挠曲线梁变形后的轴线。 性质:连续、光滑、弹性、极其平坦的平面曲线。 二、挠度横截面形心沿垂直于轴线方向的位移。 用“w”表示。w=w(X)挠度方程 挠度向上为正;向下为负。 ⊙嘉大票
第七章 弯曲变形 §7-1 引 言 一、挠曲线 梁变形后的轴线。 性质:连续、光滑、弹性、极其平坦的平面曲线。 二、挠度 横截面形心沿垂直于轴线方向的位移。 用“w” 表示。 w = w( x ) 挠度方程 挠度向上为正;向下为负。 q F x w x w 引言
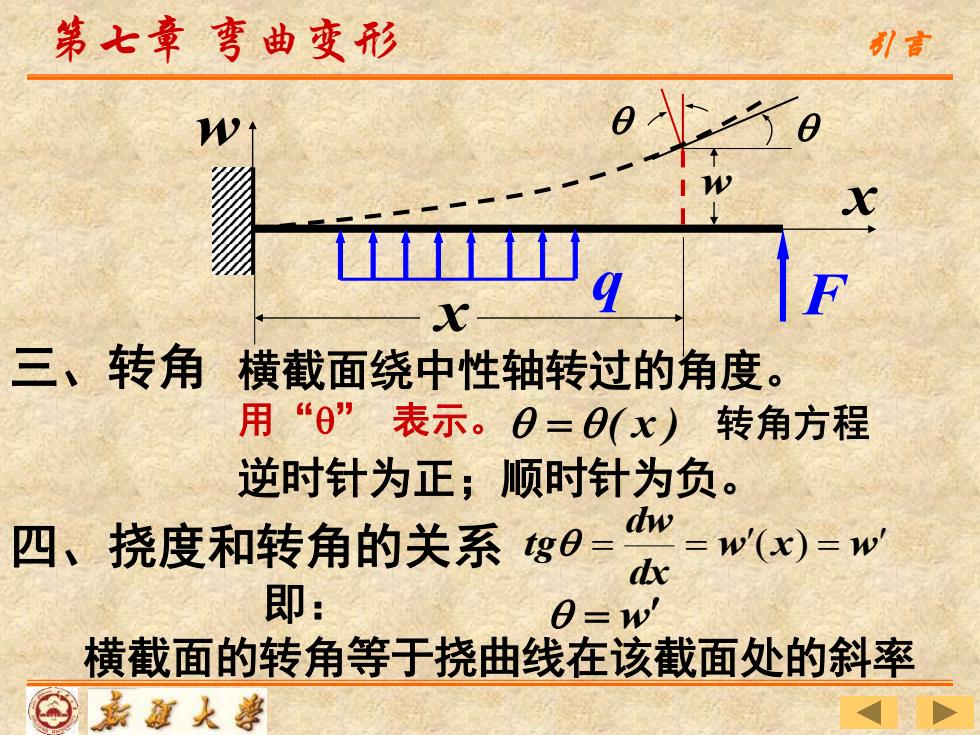
第七章弯曲变形 引言 X 三、转角 横截面绕中性轴转过的角度。 用“0”表示。0=0(x)转角方程 逆时针为正;顺时针为负。 四、挠度和转角的关系gB==w(x)=w dx 即: 0=w' 横截面的转角等于挠曲线在该截面处的斜率 ⊙老道人善
第七章 弯曲变形 三、转角 横截面绕中性轴转过的角度。 用“” 表示。 = ( x ) 转角方程 逆时针为正;顺时针为负。 四、挠度和转角的关系 q F x w x w w x w dx dw tg = = ( ) = 横截面的转角等于挠曲线在该截面处的斜率 即: = w 引言
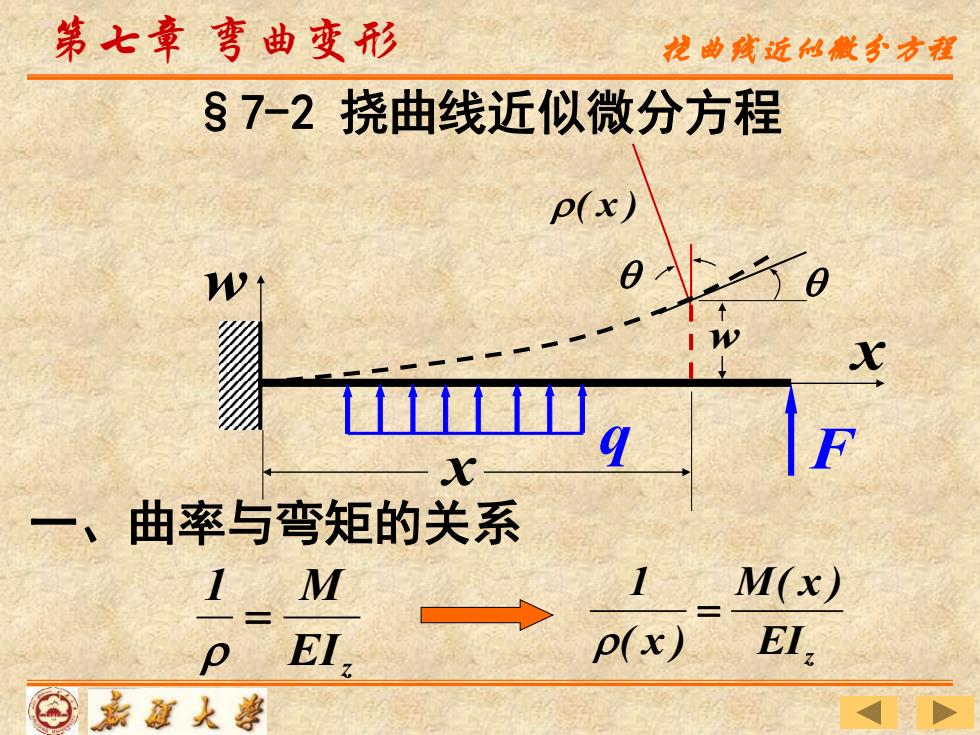
第七章弯曲变形 龙曲孩近仙般方程 §7-2挠曲线近似微分方程 p(x) W I W X X 一、曲率与弯矩的关系 1M(x) EI. p(x) EI. ⊙嘉道人
一、曲率与弯矩的关系 §7-2 挠曲线近似微分方程 第七章 弯曲变形 q F x w x w ( x ) EIz M( x ) ( x ) 1 = EIz 1 M = 挠曲线近似微分方程