
bias t⑥n is unbiased if be(⑥n)=0, 口{ a desirable property. ■⑥n is asymptotically unbiased if lim E[⑥n]= m→00 0,for every possible value of 0. becomes unbiased as the number n of observations increases, 0 this is desirable when n is large
bias Θ 𝑛 is unbiased if 𝑏𝜃 Θ 𝑛 = 0. a desirable property. Θ 𝑛 is asymptotically unbiased if lim 𝑛→∞ 𝐸𝜃 Θ 𝑛 = 𝜃, for every possible value of 𝜃. Θ𝑛 becomes unbiased as the number 𝑛 of observations increases, this is desirable when 𝑛 is large

Consistent ⑥is consistent if the sequence⑥n converges to the true value 0,in probability, for every possible value of 0. Recall: X converges to a in probability if e>0,P(|Xn-al≥e)→0,asn→o. Xn converges to a with probability 1 (or almost surely)if P(HingXn=a)=1
Consistent Θ 𝑛 is consistent if the sequence Θ 𝑛 converges to the true value 𝜃, in probability, for every possible value of 𝜃. Recall: 𝑋𝑛 converges to 𝑎 in probability if ∀𝜖 > 0, P 𝑋𝑛 − 𝑎 ≥ 𝜖 → 0, as 𝑛 → ∞. 𝑋𝑛 converges to 𝑎 with probability 1 (or almost surely) if P lim 𝑛→∞ 𝑋𝑛 = 𝑎 = 1

Mean squared error:Ee. a This is related to the bias and the variance of ⑥n:Ea[o2=b⑥n)+vara[⑥n]: o b Reason:E[X2]=(E[X])2+var(X),X=δn=⑥n-0. In many statistical problems,there is a tradeoff between the two terms on the right-hand-side. Often a reduction in the variance is accompanied by an increase in the bias. Of course,a good estimator is one that manages to keep both terms small
Mean squared error: 𝐸𝜃 Θ෩𝑛 2 . This is related to the bias and the variance of Θ 𝑛: 𝐸𝜃 Θ෩𝑛 2 = 𝑏𝜃 2 Θ 𝑛 + 𝑣𝑎𝑟𝜃 Θ 𝑛 . Reason: 𝐸 𝑋 2 = 𝐸 𝑋 2 + 𝑣𝑎𝑟(𝑋), 𝑋 = Θ෩𝑛 = Θ𝑛 − 𝜃. In many statistical problems, there is a tradeoff between the two terms on the right-hand-side. Often a reduction in the variance is accompanied by an increase in the bias. Of course, a good estimator is one that manages to keep both terms small

Maximum Likelihood Estimation (MLE) Let the vector of observations (X1,...,Xn) be described by a joint PMF px(x;0) Note that px(x;0)is PMF for X only,not joint distribution for X and 0. Recall 0 is just a fixed parameter,not a random variable. px(x;θ)depends on 0. Suppose we observe a particular value x (x1,.,Xn)0fX
Maximum Likelihood Estimation (MLE) Let the vector of observations 𝑋 = 𝑋1, … , 𝑋𝑛 be described by a joint PMF 𝑝𝑋 𝑥; 𝜃 Note that 𝑝𝑋 𝑥; 𝜃 is PMF for 𝑋 only, not joint distribution for 𝑋 and 𝜃. Recall 𝜃 is just a fixed parameter, not a random variable. 𝑝𝑋 𝑥; 𝜃 depends on 𝜃. Suppose we observe a particular value 𝑥 = 𝑥1, … , 𝑥𝑛 of 𝑋
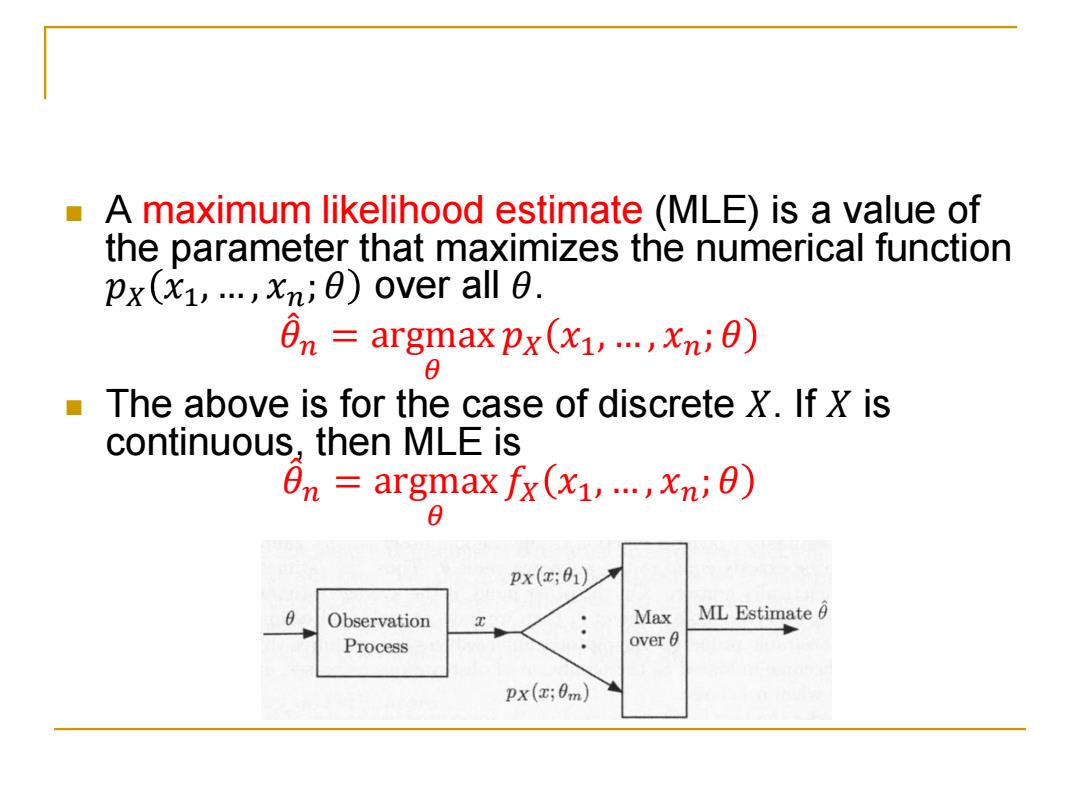
A maximum likelihood estimate(MLE)is a value of the parameter that maximizes the numerical function px(1,...,x;)over all e. en argmax px(x1,..,xn) The above is for the case of discrete X.If X is continuous,then MLE is en argmax fx (x1,...,xn;) 0 px(x;01) Observation Max ML Estimate 6 Process over 0 px(x;0m)
A maximum likelihood estimate (MLE) is a value of the parameter that maximizes the numerical function 𝑝𝑋 𝑥1, … , 𝑥𝑛; 𝜃 over all 𝜃. 𝜃መ 𝑛 = argmax 𝜃 𝑝𝑋 𝑥1, … , 𝑥𝑛; 𝜃 The above is for the case of discrete 𝑋. If 𝑋 is continuous, then MLE is 𝜃መ 𝑛 = argmax 𝜃 𝑓𝑋 𝑥1, … , 𝑥𝑛; 𝜃