
1、截尾处理: 1)正数(三种码形式相同) 一个b,位的正数x为: 立 i=l 用表示截尾处理,则 [r=∑B,21 i=l return
1、截尾处理: 1)正数(三种码形式相同) 一个b1位的正数 为: 用[·]T表示截尾处理,则 ∑ = − = 1 1 2 b i i i x β ∑ = − = b i i T i x 1 [ ] β 2 x return

截尾误差 E,=[x]r-x= 一 B2-1 i=b+1 可见,E≤0,全为1时,E有最大值, E,=-22i=-2-2) i=b+1 “量化宽度”或“量化阶”q=2b:代表b位字长可 表示的最小数。 一般2-b1<<2b,因此正数的截尾误差为 -q≤Em≤0 return
截尾误差 可见,ET≤0,βi 全为1时,ET有最大值, “量化宽度”或“量化阶” q=2-b :代表b位字长可 表示的最小数。 一般 2-b1<<2-b , 因此正数的截尾误差为 -q≤ET≤0 ∑ = + − = − = − 1 1 [ ] 2 b i b i i E x x T T β 2 (2 2 ) 1 1 1 b b b i b T i E − − = + = − − − = − ∑ return

2)负数 负数的三种码表示方式不同,所以误差也不同 原码(=1): b x=- 2g2 [xl B.21 i-l = i 5,=Kl-x=2A2 i=b+1 0sE≤q return
2)负数 负数的三种码表示方式不同,所以误差也不同 。 原码(β0=1): 0≤ET≤q ∑ = − = − 1 1 2 b i i i x β ∑ = − = − b i i i 1 2 T [x] β [ ] ∑ = + − = − = 1 1 2 b i b i T T i E x x β return
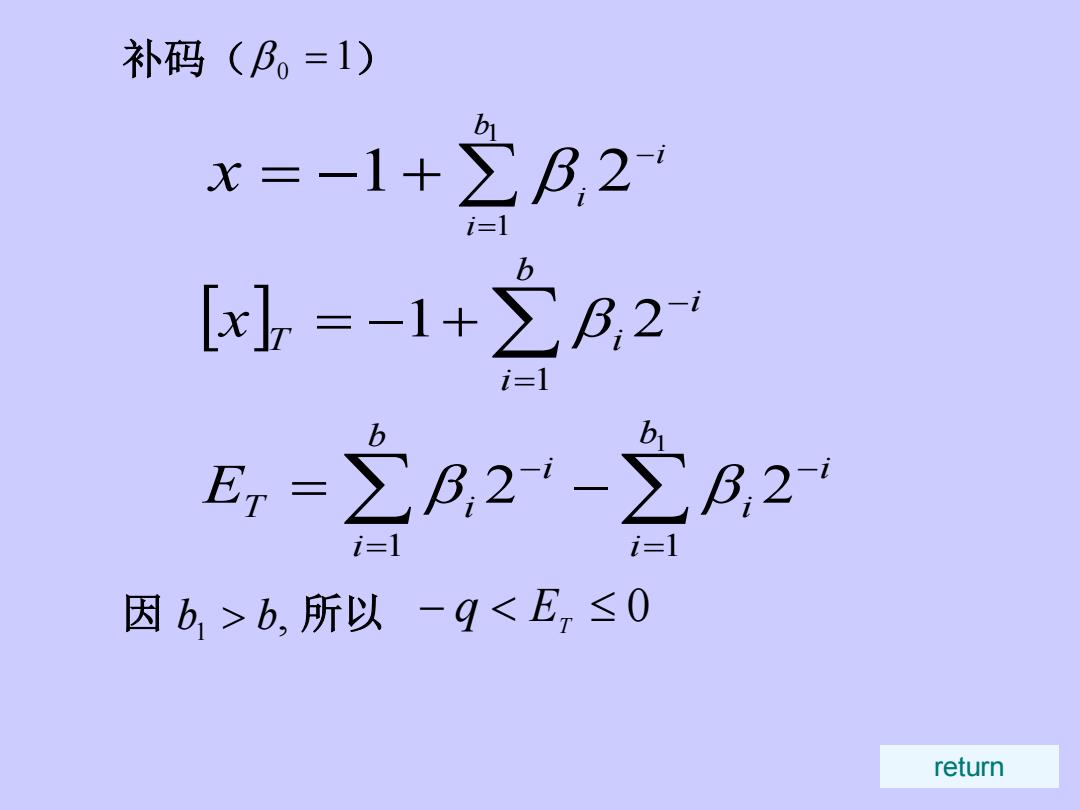
补码(B=1) x=-1+2B,2 i=1 []-1+2A2 i三l E,-2A2-之月2 i=1 i=1 因b>b,所以-9<E,≤0 return
补码( ) 因 所以 1 β 0 = ∑ = − = − + 1 1 1 2 b i i i x β [ ] ∑ ∑ ∑ = = − − = − = − = − + b i b i i i i T i b i i T i E x 1 1 1 1 2 2 1 2 β β β , 1 b > b − < ≤ 0 ET q return

反码(P。=1) x=-1+2A2+24 i1 [,=-1+B2+2 E,=x-x=-2B,2+(2-2) i=b+1 0≤ E,<q(E,>0与原码的相同) return
反码( ) ( 与原码的相同) [ ] [ ] 2 (2 2 ) 1 2 2 1 2 2 1 1 1 1 1 1 1 ∑ ∑ ∑ = + − − − = − − = − − = − = − + − = − + + = − + + b i b i b b T T i b i i b T i b i i b i E x x x x β β β 1 β 0 = E q 0 ≤ T < > 0 ET return