Sampling and Inference for Big Data ●Sampling from a joint distribution (specified by a probabilistic graphical model). ● Inferring according to a probabilistic graphical model. The data (probabilistic graphical model)is BIG
Sampling and Inference for Big Data • Sampling from a joint distribution (specified by a probabilistic graphical model). • Inferring according to a probabilistic graphical model. • The data (probabilistic graphical model) is BIG

Parallel/distributed algorithms for sampling? ·PTIME→Polylog(n)rounds o For parallel/distributed computing: sampling approx counting/inference? 0 PTIME=Polylog(n)rounds √●Dynamic sampling algorithms2 PTIME Polylog(n)incremental cost
• Parallel/distributed algorithms for sampling? • For parallel/distributed computing: sampling ≡ approx counting/inference? • Dynamic sampling algorithms? ✓ ✓ ✓ • PTIME ⟹ Polylog(n) rounds • PTIME ⟹ Polylog(n) rounds • PTIME ⟹ Polylog(n) incremental cost
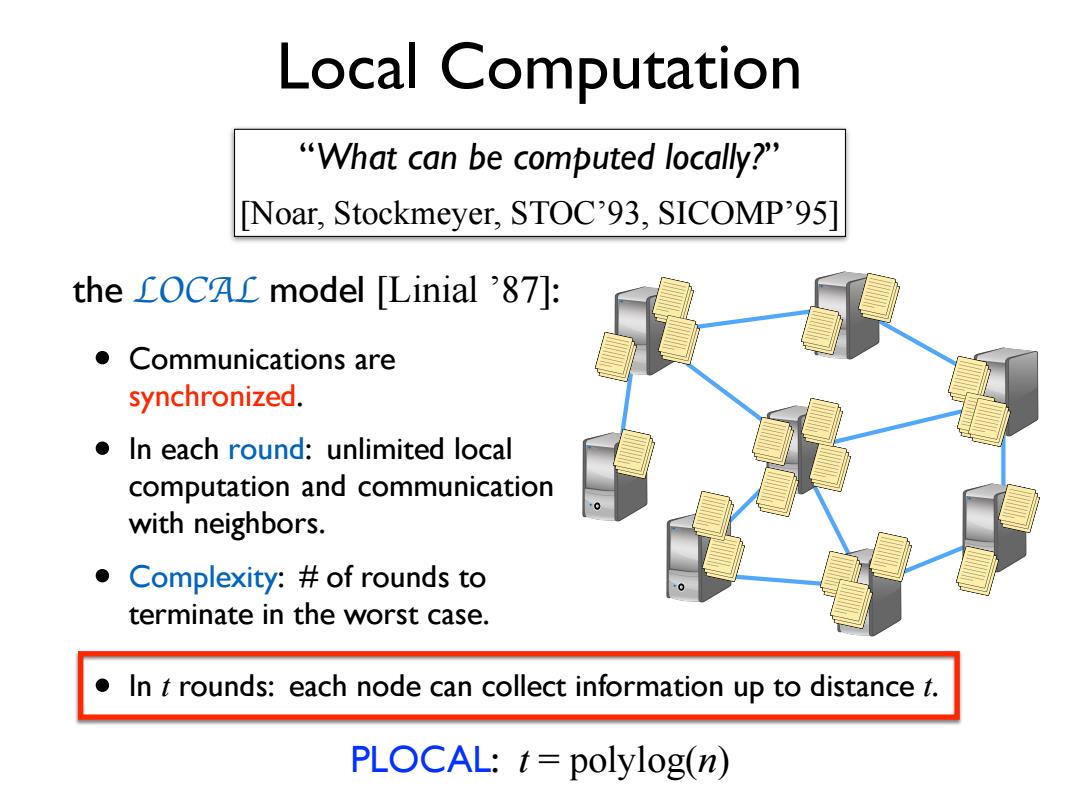
Local Computation "What can be computed locally?" [Noar,Stockmeyer,STOC'93,SICOMP'95] the LOCAC model [Linial '87]: ● Communications are synchronized. In each round:unlimited local computation and communication with neighbors. Complexity:of rounds to 0 terminate in the worst case. In t rounds:each node can collect information up to distance t. PLOCAL:t=polylog(n)
Local Computation • Communications are synchronized. • In each round: unlimited local computation and communication with neighbors. • Complexity: # of rounds to terminate in the worst case. • In t rounds: each node can collect information up to distance t. the LOCAL model [Linial ’87]: “What can be computed locally?” [Noar, Stockmeyer, STOC’93, SICOMP’95] PLOCAL: t = polylog(n)

"What can be sampled locally?" Joint distribution defined by local constraints: ●Markov random field ●Graphical model .Sample a random solution from the joint distribution: distributed algorithms (in the LOCAC model) network G(,E) Q:"What locally definable joint distributions are locally sample-able?
“What can be sampled locally?” network G(V,E) • Joint distribution defined by local constraints: • Markov random field • Graphical model • Sample a random solution from the joint distribution: • distributed algorithms (in the LOCAL model) Q: “What locally definable joint distributions are locally sample-able?
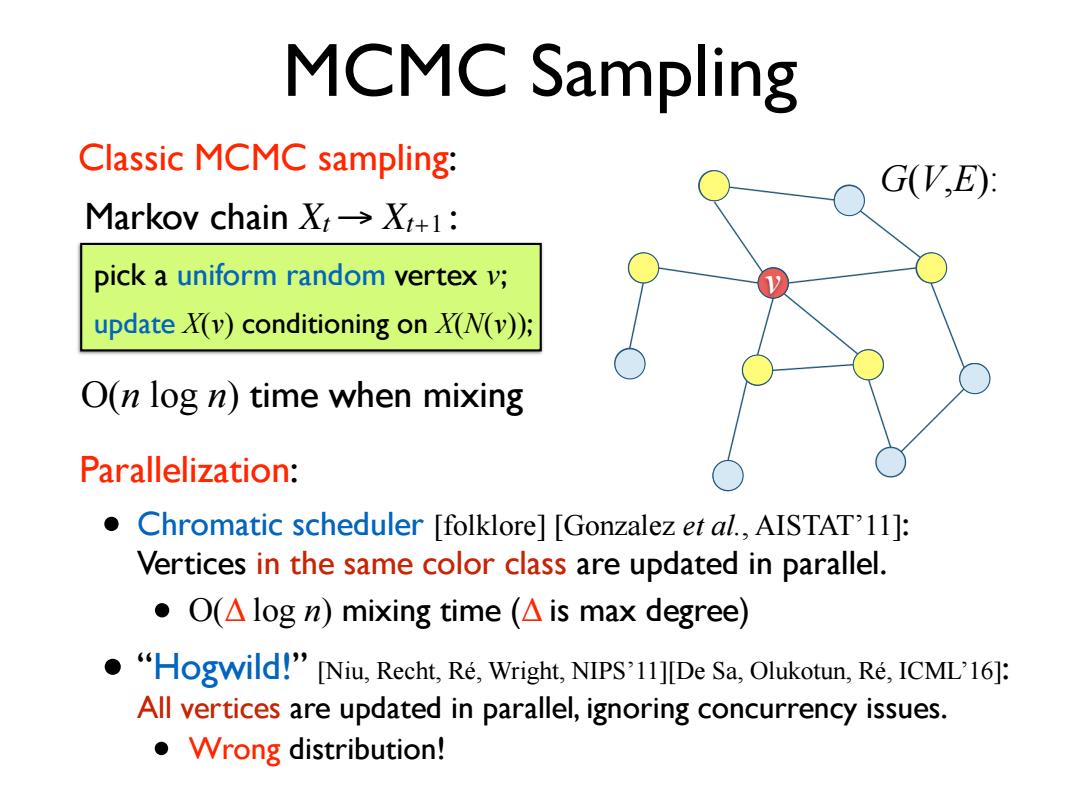
MCMC Sampling Classic MCMC sampling: GV,E) Markoy chain X→X+l: pick a uniform random vertex v; update X(v)conditioning on X(N(v)); O(n log n)time when mixing Parallelization: Chromatic scheduler [folklore][Gonzalez et al.,AISTAT'11]: Vertices in the same color class are updated in parallel. ●O△logn)mixing time(△is max degree) "Hogwild!"[Niu,Recht,Re.Wright,NIPS'11][De Sa,Olukotun,Re,ICML'16]: All vertices are updated in parallel,ignoring concurrency issues. ●Wrong distribution!
MCMC Sampling G(V,E): v Classic MCMC sampling: Parallelization: • Chromatic scheduler [folklore] [Gonzalez et al., AISTAT’11]: Vertices in the same color class are updated in parallel. • “Hogwild!” [Niu, Recht, Ré, Wright, NIPS’11][De Sa, Olukotun, Ré, ICML’16]: All vertices are updated in parallel, ignoring concurrency issues. pick a uniform random vertex v; update X(v) conditioning on X(N(v)); Markov chain Xt → Xt+1 : O(n log n) time when mixing • O(Δ log n) mixing time (Δ is max degree) • Wrong distribution!