
The Poisson Random Variable A Poisson random variable takes nonnegative integer values. The PMF px(k)=e k! k=0,1,2,., Normalization condition 宽=(++云+ 00 k=0 =e-e1=1
The Poisson Random Variable ◼ A Poisson random variable takes nonnegative integer values. ◼ The PMF 𝑝𝑋 𝑘 = 𝑒 −𝜆 𝜆 𝑘 𝑘! ,𝑘 = 0, 1, 2, …, ◼ Normalization condition 𝑘=0 ∞ 𝑒 −𝜆 𝜆 𝑘 𝑘! = 𝑒 −𝜆 1 + 𝜆 + 𝜆 2 2! + 𝜆 3 3! + ⋯ = 𝑒 −𝜆 𝑒 𝜆 = 1

Poisson random variable can be viewed as a binomial random variable with very small p and very large n. More precisely,the Poisson PMF with parameter A is a good approximation for a binomial PMF with parameters n and p where 1 =np,n is large and p is small. See the wiki page for a proof
◼ Poisson random variable can be viewed as a binomial random variable with very small 𝑝 and very large 𝑛. ◼ More precisely, the Poisson PMF with parameter 𝜆 is a good approximation for a binomial PMF with parameters 𝑛 and 𝑝 where 𝜆 = 𝑛𝑝, 𝑛 is large and 𝑝 is small. ❑ See the wiki page for a proof

Examples Because of the above connection,Poisson random variables are used in many scenarios. X is the number of typos in a book of n words. The probability that any one word is misspelled is very small. X is the number of cars involved in accidents in a city on a given day. 0 The probability that any one car is involved in an accident is very small
Examples ◼ Because of the above connection, Poisson random variables are used in many scenarios. ◼ 𝑋 is the number of typos in a book of 𝑛 words. ❑ The probability that any one word is misspelled is very small. ◼ 𝑋 is the number of cars involved in accidents in a city on a given day. ❑ The probability that any one car is involved in an accident is very small
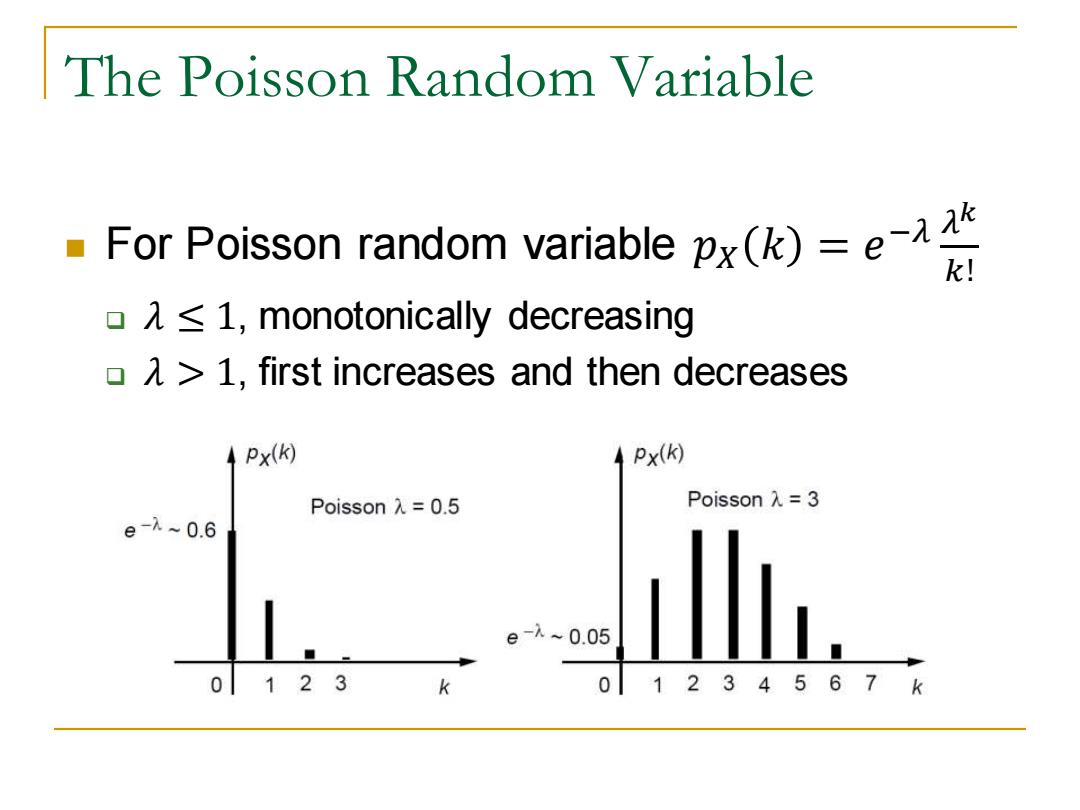
The Poisson Random Variable For Poisson random variable px(k)=e k! oz≤1,monotonically decreasing 1,first increases and then decreases Px(k) Px(k) Poisson入=0.5 Poissonλ=3 e-1~0.6 e-1~0.05 l 0123 01234567
The Poisson Random Variable ◼ For Poisson random variable 𝑝𝑋 𝑘 = 𝑒 −𝜆 𝜆 𝑘 𝑘! ❑ 𝜆 ≤ 1, monotonically decreasing ❑ 𝜆 > 1, first increases and then decreases

Content Basic Concepts Probability Mass Function Functions of Random variables ■ Expectation,Mean,and Variance Joint PMFs of Multiple Random Variables Conditioning Independence
Content ◼ Basic Concepts ◼ Probability Mass Function ◼ Functions of Random Variables ◼ Expectation, Mean, and Variance ◼ Joint PMFs of Multiple Random Variables ◼ Conditioning ◼ Independence