
The Binomial Random Variable We refer to X as a binomial random variable with parameters n and p. For k =0,1,...,n. px(=pX=)=()*(1-m-k
The Binomial Random Variable ◼ We refer to 𝑋 as a binomial random variable with parameters 𝑛 and 𝑝. ◼ For 𝑘 = 0,1, …, 𝑛. 𝑝𝑋 𝑘 = 𝑃 𝑋 = 𝑘 = 𝑛 𝑘 𝑝 𝑘 1 − 𝑝 𝑛−𝑘
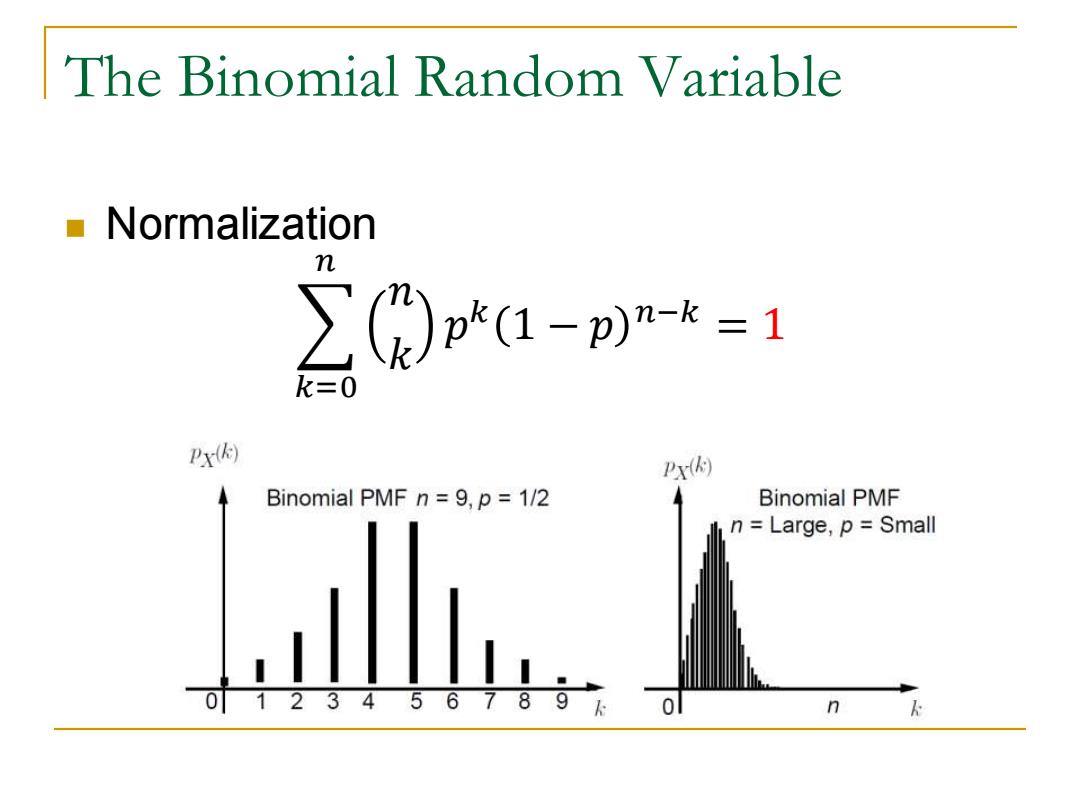
The Binomial Random Variable Normalization ∑((1-p-*=1 k=0 x网 r Binomial PMF n 9,p=1/2 Binomial PMF n Large,p=Small adla 0123456789k 0 n
The Binomial Random Variable ◼ Normalization 𝑘=0 𝑛 𝑛 𝑘 𝑝 𝑘 1 − 𝑝 𝑛−𝑘 = 1

The Geometric Random Variable Independently and repeatedly toss a biased coin with probability of a head p,where 0< p<1. The geometric random variable is the number X of tosses needed for a head to come up for the first time
The Geometric Random Variable ◼ Independently and repeatedly toss a biased coin with probability of a head 𝑝, where 0 < 𝑝 < 1. ◼ The geometric random variable is the number 𝑋 of tosses needed for a head to come up for the first time

The Geometric Random Variable The PMF of a geometric random variable px(k)=(1-p)k-1p k-1 tails followed by a head. Normalization condition is satisfied: 00 ∑prW)=∑1-p)-p=p∑1-p) k=1 k=0 1 =p 1-(1-=1
The Geometric Random Variable ◼ The PMF of a geometric random variable 𝑝𝑋 𝑘 = 1 − 𝑝 𝑘−1𝑝 ❑ 𝑘 − 1 tails followed by a head. ◼ Normalization condition is satisfied: 𝑘=1 ∞ 𝑝𝑋 𝑘 = 𝑘=1 ∞ 1 − 𝑝 𝑘−1𝑝 = 𝑝 𝑘=0 ∞ 1 − 𝑝 𝑘 = 𝑝 ⋅ 1 1− 1−𝑝 = 1
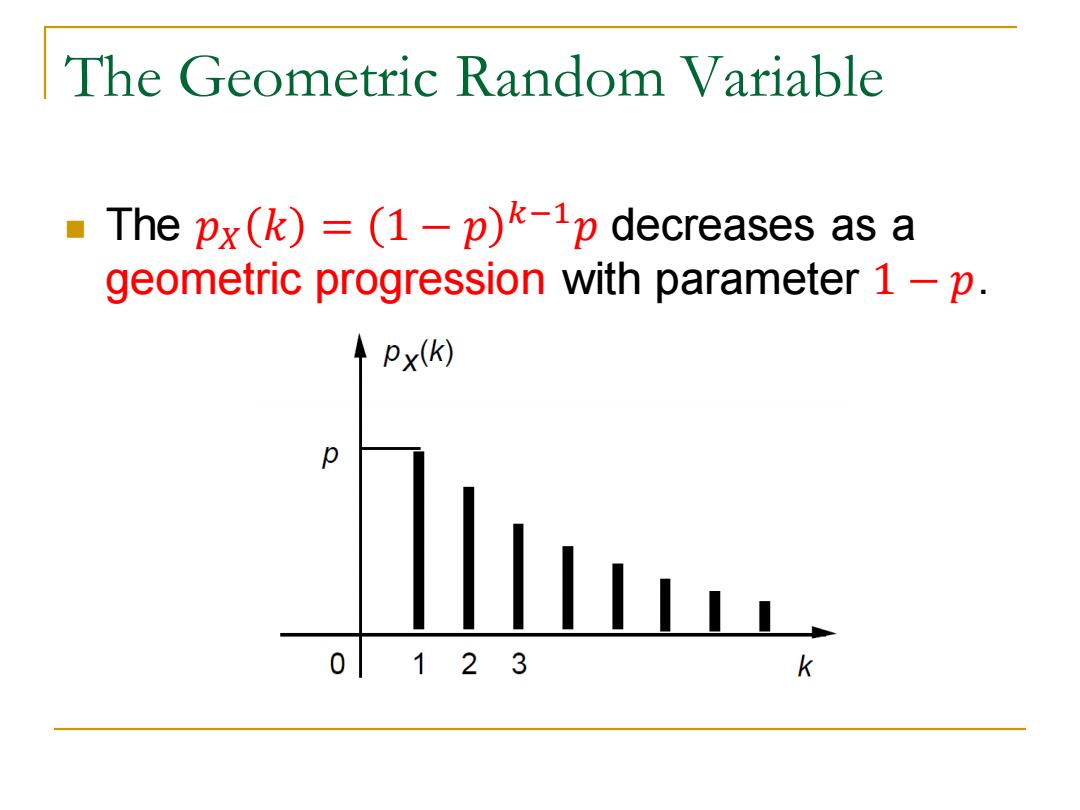
The Geometric Random Variable The px(k)=(1-p)k-Ip decreases as a geometric progression with parameter 1 -p. px(k) 0123
The Geometric Random Variable ◼ The 𝑝𝑋 𝑘 = 1 − 𝑝 𝑘−1𝑝 decreases as a geometric progression with parameter 1 − 𝑝