任意可逆循环的热温商Rp个ITPVO= OWQPOQWMXO'= O'YNXY0MUSV任意可逆循环
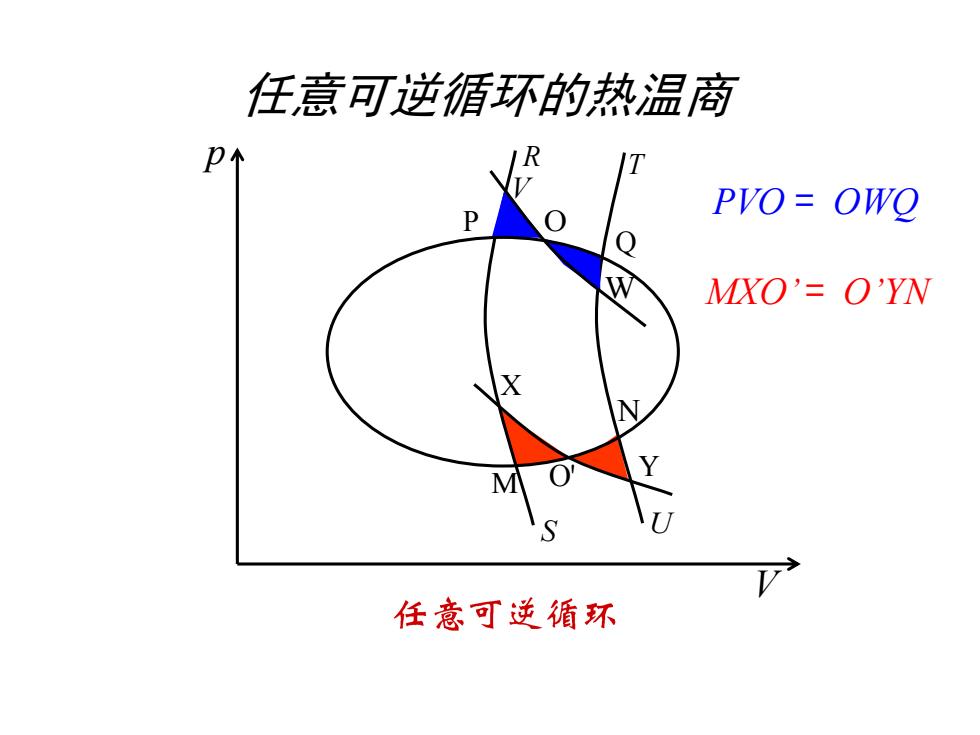
任意可逆循环的热温商 p V P Q M N X O' Y T U R S O V W PVO = OWQ MXO’ = O’YN
任意可逆循环的热温商用相同的方法把任意可逆循环分成许多首尾连接的小卡-诺循环,前一个循环的绝热可逆膨胀线就是下一个循环的绝热可逆压缩线,如图所示的虚CG线部分,这样两个过程的功恰图2.4一连串卡诺循环好抵消。从而使众多小卡诺循环的总效应与任意可逆循环的封闭曲线相当,所以任意可逆循环的热温商的加和等于零,或它的环程积分等于零
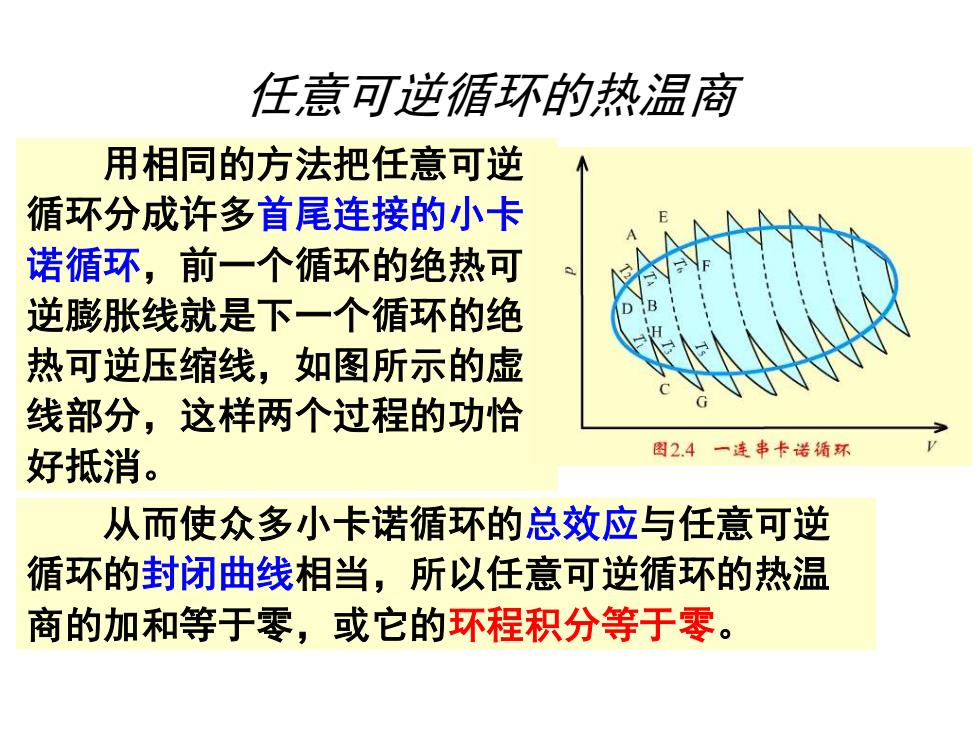
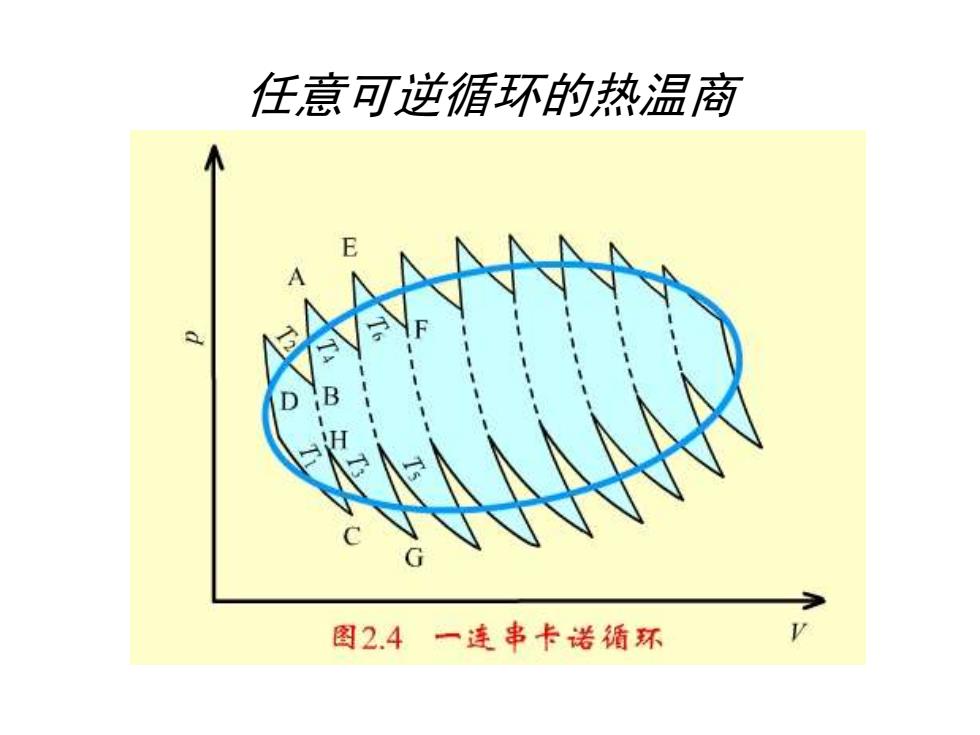
任意可逆循环的热温商 用相同的方法把任意可逆 循环分成许多首尾连接的小卡 诺循环,前一个循环的绝热可 逆膨胀线就是下一个循环的绝 热可逆压缩线,如图所示的虚 线部分,这样两个过程的功恰 好抵消。 从而使众多小卡诺循环的总效应与任意可逆 循环的封闭曲线相当,所以任意可逆循环的热温 商的加和等于零,或它的环程积分等于零
任意可逆循环的热温商-C图2.4一连串卡诺循环
任意可逆循环的热温商

而每个小卡诺循环的热温商之和为零8080;80Z0TTT,6Qi=8Q.Z=p=0T:T
i i Q Q Q T T T + + = = 1 2 1 2 0 i i Q T = Qr T = 0 而每个小卡诺循环的热温商之和为零
的引出2.任意可逆循环用一闭合曲线代表任意可逆循环。在曲线上任意取A,B两点,把循环分成A→B和B一A两个可逆过程。根据任意可逆循环热温商的公式:8911TR2Ri将上式分成两项的加和B()R, +JR任意可逆循环7
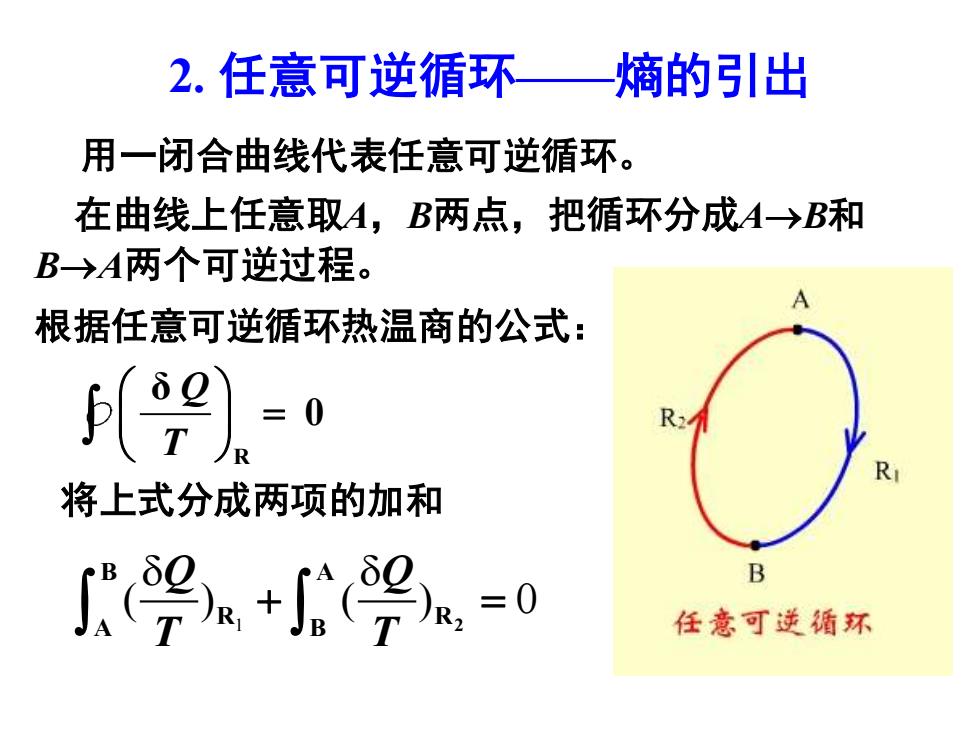
2. 任意可逆循环——熵的引出 用一闭合曲线代表任意可逆循环。 1 ( ) ( ) 0 Q Q T T + = 2 B A R R A B 将上式分成两项的加和 在曲线上任意取A,B两点,把循环分成A→B和 B→A两个可逆过程。 根据任意可逆循环热温商的公式: Q T = R δ 0