
回归分析 ·什么是回归分析? ·简单回归分析(一个自变量) ·多元回归分析(多个自变量) ·具体应用场景: ·市场分析:销量预测 ·心理学:满意度分析 16
回归分析 • 什么是回归分析? • 简单回归分析 (一个自变量) • 多元回归分析 (多个自变量) • 具体应用场景: • 市场分析: 销量预测 • 心理学: 满意度分析 16
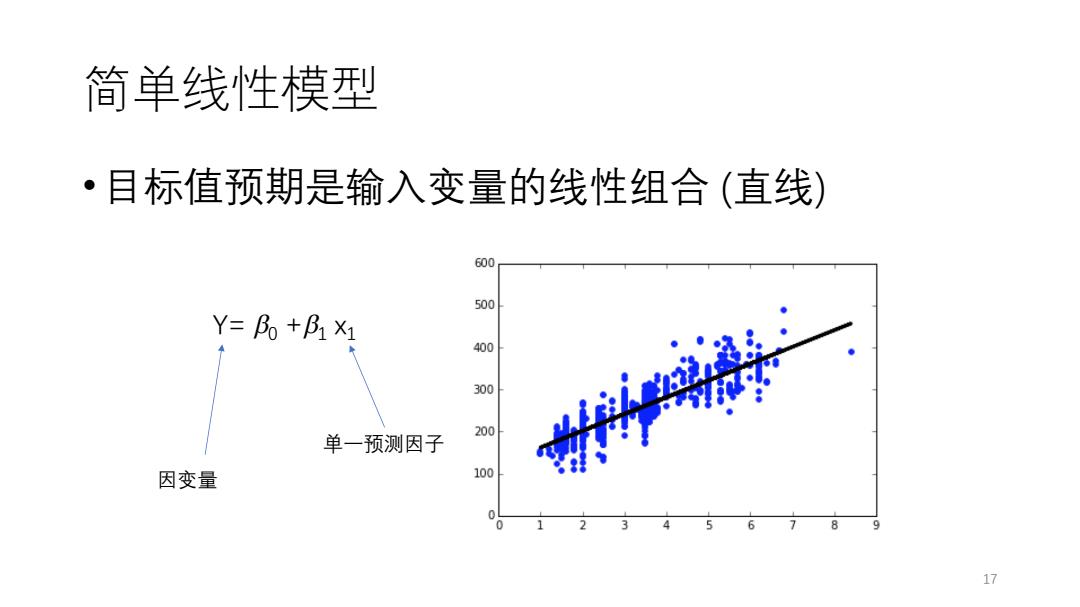
简单线性模型 ·目标值预期是输入变量的线性组合(直线) 600 500 Y=阝+P11 400 300 200 单一预测因子 因变量 100 17
简单线性模型 •目标值预期是输入变量的线性组合 (直线) 17 Y= b0 +b1 瀋1 单一预测因子 因变量
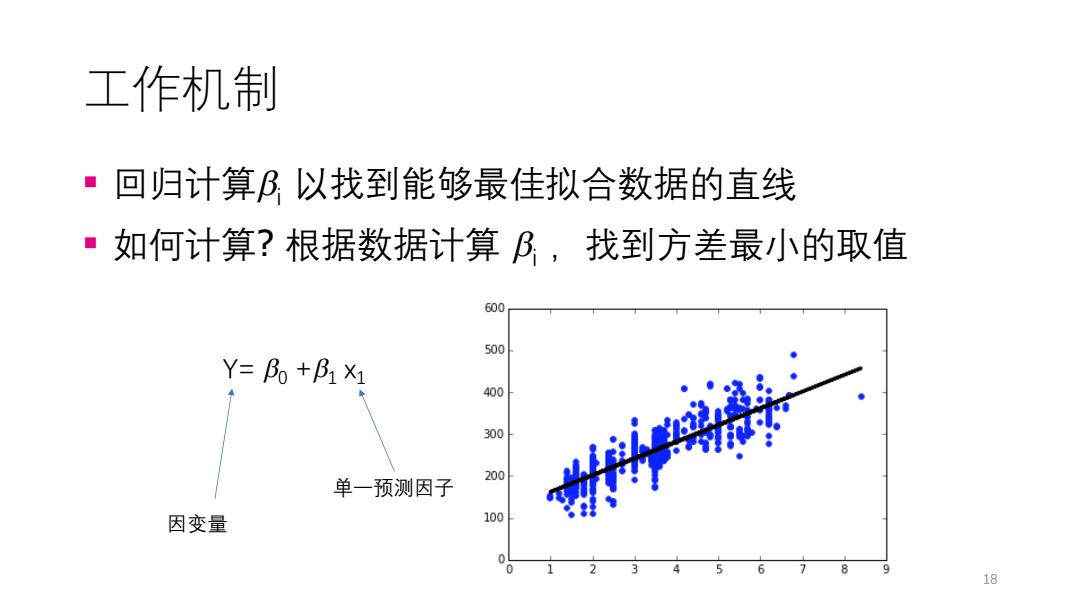
工作机制 ·回归计算阝以找到能够最佳拟合数据的直线 ·如何计算?根据数据计算B,找到方差最小的取值 600 500 Y=B+B1×1 400 300 200 单一预测因子 因变量 100 18
工作机制 § 回归计算bi 以找到能够最佳拟合数据的直线 § 如何计算? 根据数据计算 bi ,找到方差最小的取值 18 Y= b0 +b1 瀋1 单一预测因子 因变量
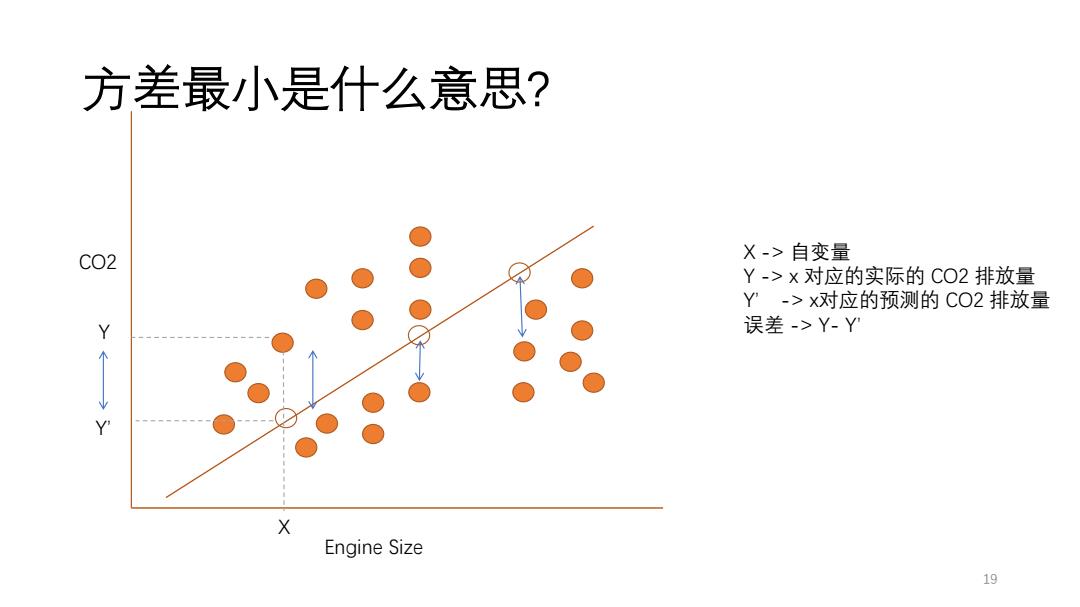
方差最小是什么意思? CO2 X->自变量 Y->x对应的实际的CO2排放量 Y->x对应的预测的CO2排放量 Y 误差->Y-Y X Engine Size 19
方差最小是什么意思? 19 Y Y’ E瀁gi瀁e Si瀍e CO2 X -> 自变量 Y -> 瀋 对应的实际的 CO2 排放量 Y’ -> 瀋对应的预测的 CO2 排放量 误差 -> Y- Y’ X

最小二乘法线性回归 ·线性回归拟合系数为B=(B,阝2)的线性模型 可以最小化数据集中观测到的响应值()与由线性近似预测的响应值() 之间的残差平方和 ·在数学上讲,它可以解决下面形式的问题: MIN∑.Oy,-xB2 i=1 20
最小二乘法线性回归 • 线性回归拟合系数为b = (b1, b2,..)的线性模型 • 可以最小化数据集中观测到的响应值 (Y) 与由线性近似预测的响应值(Y') 之间的残差平方和 • 在数学上讲,它可以解决下面形式的问题: ���$(�' − �'�), - './ 20