
例1图示悬臂梁受集度为g的满布均布荷载作用。试 作梁的剪力图和弯矩图。 B 解:1、以自由端为坐标原点,则可不求反力 列剪力方程和弯矩方程: F(x)=gx(0≤x<I) Fs(x) )-于-50<
例1 图示悬臂梁受集度为q的满布均布荷载作用。试 作梁的剪力图和弯矩图。 解:1、以自由端为坐标原点,则可不求反力 列剪力方程和弯矩方程: F (x) = qx(0 x l) S ( ) ( x l) x qx M x = −qx = − 0 2 2 2 A B x l B x FS (x) M(x)
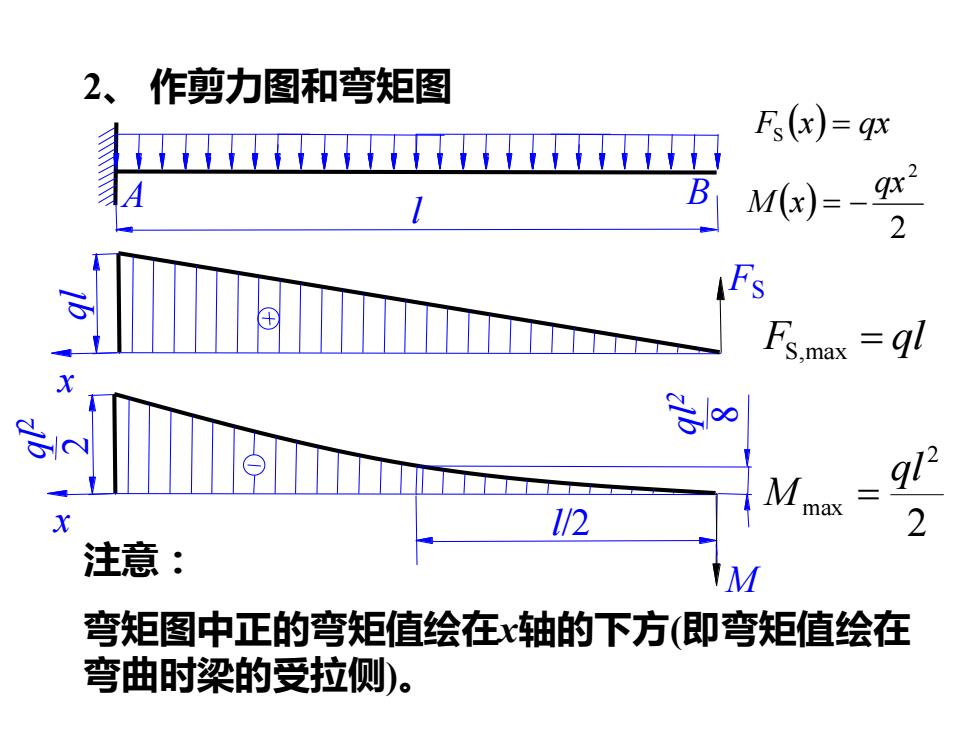
2、作剪力图和弯矩图 Fs(x)=qx Mx)=-9 2 ⊕ Fs.nax =gl M 9/2 1/2 ax 注意: 弯矩图中正的弯矩值绘在x轴的下方(即弯矩值绘在 弯曲时梁的受拉侧)
2、 作剪力图和弯矩图 注意: 弯矩图中正的弯矩值绘在x轴的下方(即弯矩值绘在 弯曲时梁的受拉侧)。 F (x) = qx S ( ) 2 2 qx M x = − x ql FS ql 2 2 x M l/2 ql 2 8 A B l F = ql S,max 2 2 max ql M =
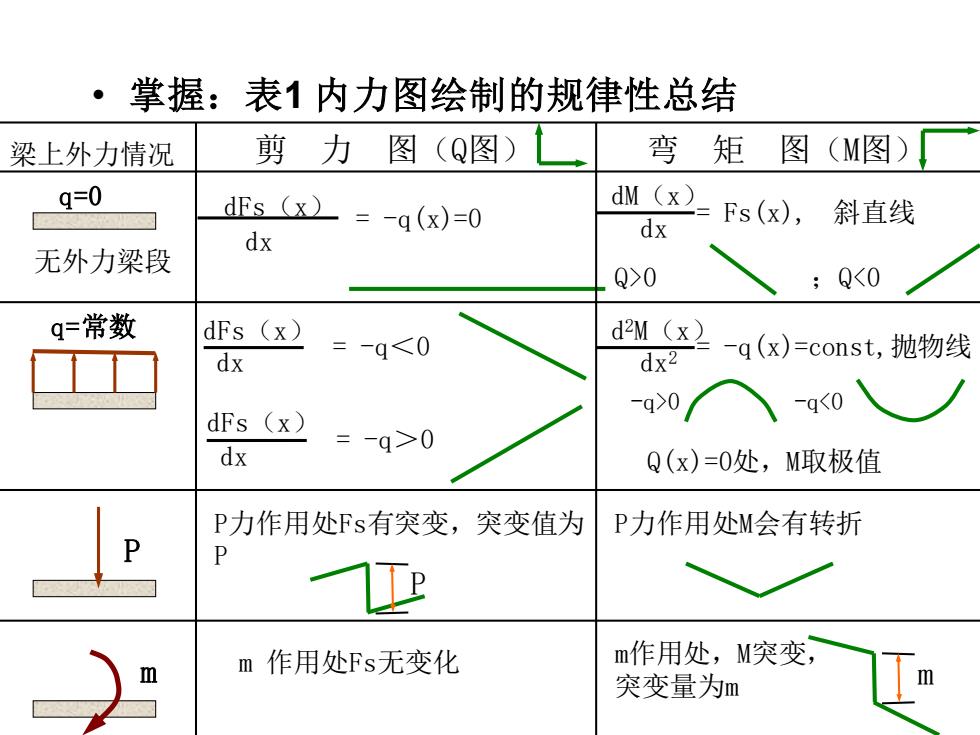
掌握:表1内力图绘制的规律性总结 梁上外力情况 剪 力图(Q图) 弯 矩 图(M图) q=0 dEs (x)=-q(x)=0 dM (x>= s(x),斜直线 dx dx 无外力梁段 Q>0 ;Q<0 q=常数 dFs (x) =-q<0 d2M(x dx dx2 :-q(x)=const,抛物线 -q>0/ -q<0 dFs (x) =-q>0 dx Q(x)=0处,M取极值 P力作用处Fs有突变,突变值为 P力作用处M会有转折 P m m作用处Fs无变化 m作用处,M突变, 突变量为m
• 掌握:表1 内力图绘制的规律性总结 P m q=常数 q=0 无外力梁段 dFs(x) dx = -q(x)=0 dM(x) dx = Fs(x), 斜直线 Q>0 ;Q<0 梁上外力情况 剪 力 图(Q图) 弯 矩 图(M图) dFs(x) dx = -q<0 dFs(x) dx = -q>0 d 2M(x) dx2 = -q(x)=const,抛物线 -q>0 -q<0 Q(x)=0处,M取极值 P力作用处Fs有突变,突变值为 P P P力作用处M会有转折 m 作用处Fs无变化 m作用处,M突变, 突变量为m m
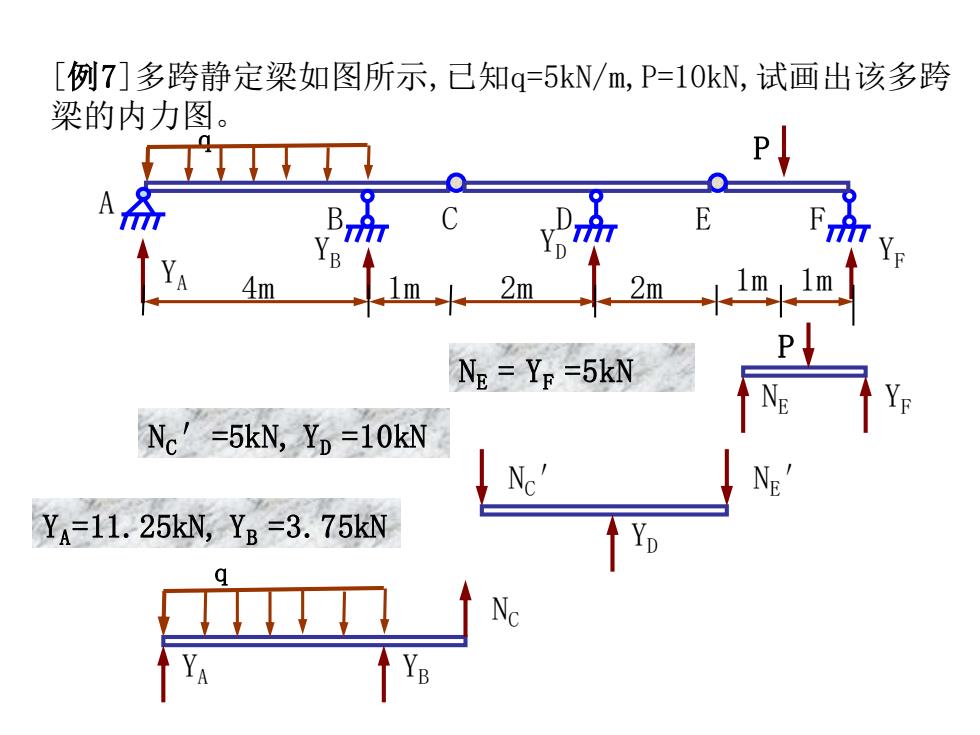
[例7]多跨静定梁如图所示,已知q=5kN/m,P=10kN,试画出该多跨 梁的内力图。 Q A 4m -2 2m NE Ye =5kN Nc′=5kN,YD=10kN Ne' YA=11.25kN,YB=3.75kN YA
[例7]多跨静定梁如图所示,已知q=5kN/m,P=10kN,试画出该多跨 梁的内力图。 P q YF Y YD B YA 4m 1m 2m 2m 1m 1m E F A B C D YF P NE YA YB q NC YD NC ′ NE ′ NE = YF =5kN NC′=5kN, YD =10kN YA=11.25kN, YB =3.75kN
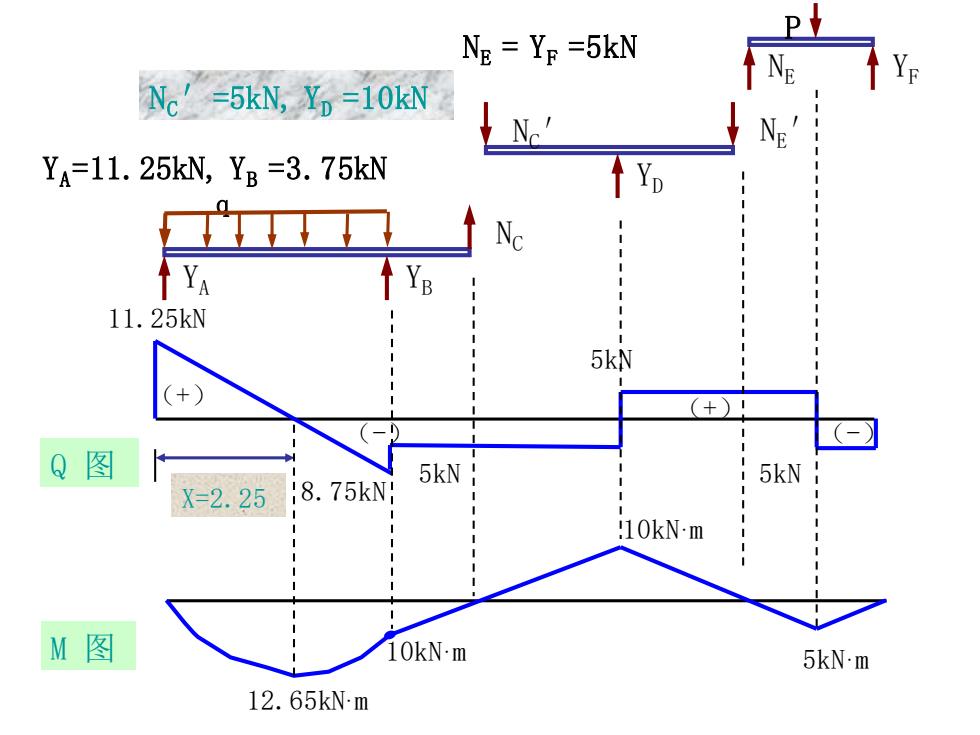
D Ne Yp =5kN Ne′=5kN,YD=10kN Ya=11.25kN,Yg=3.75kN Y Ya ↑YB 11.25kN 5kN (+)I Q图 5kN i X=2.258.75kN 5kN :10kN-m M图 10kN-m 5kN.m 12.65kNm
M 图 10kN·m 10kN·m YF P NE YA YB q NC YD NC ′ NE ′ NE = YF =5kN NC′=5kN, YD =10kN YA=11.25kN, YB =3.75kN 5kN 8.75kN (-) Q 图 11.25kN (+) (-) (+) 5kN 5kN 12.65kN·m 5kN·m X=2.25