
类氢原子的解 平nm(r,0,)=Ru(r)Ym(O,p) E、 2n(a0 n=1,2,3,… 1=0,1,2,…,n-1 m=0,±1,±2,…,±1 21+1 2m-1m 可能的微态数=品色×n=m 即对于类氢体系,体系的简并度为n2. 量子数n12 3 4 原子轨道ss,p(3)s,p(3),d(5)s,p(3),d5),f7)… 波函数的性质 径向分布:(1)Rsr作图:(2)R2sr作图:(3)2R2sr作 图(D=4πr2R). 物理意义:R表明在距核为r的大圆球面上电子的几率; R川4πd表明在距核为r厚度为d的球壳内找到电子的几率, i.e.R4m表明在距核为r单位厚度的球壳内找到电子的几率
类氢原子的解 ( ,θ ,φ) ( ) (θ ,φ) nlm nl Ylm Ψ r = R r ( . ) 2 2 2 a u n Z E == − m l l n n = ± ± ± = − = 0, 1, 2, , 0, 1, 2, , 1 1, 2, 3, " " " n l 0 1 2 n-1 2l+1 1 3 5 2n-1 m 1 n 2 n n 2 a a × = + 可能的微态数 = 即对于类氢体系,体系的简并度为 n 2 . 量子数 n 1 2 3 4 … 原子轨道 s s, p(3) s, p(3), d(5) s, p(3), d(5), f(7) … 波函数的性质 径向分布: (1)R vs r 作图;(2)R2 vs r 作图;(3)r 2 R2 vs r 作 图 (D=4πr 2 R2 ). 物理意义: |Rnl(r)|2 表明在距核为 r 的大圆球面上电子的几率; |Rnl(r)|2 ⋅4πr 2 dr 表明在距核为 r 厚度为 dr 的球壳内找到电子的几率, i.e. |Rnl(r)|2 ⋅4πr 2表明在距核为 r 单位厚度的球壳内找到电子的几率
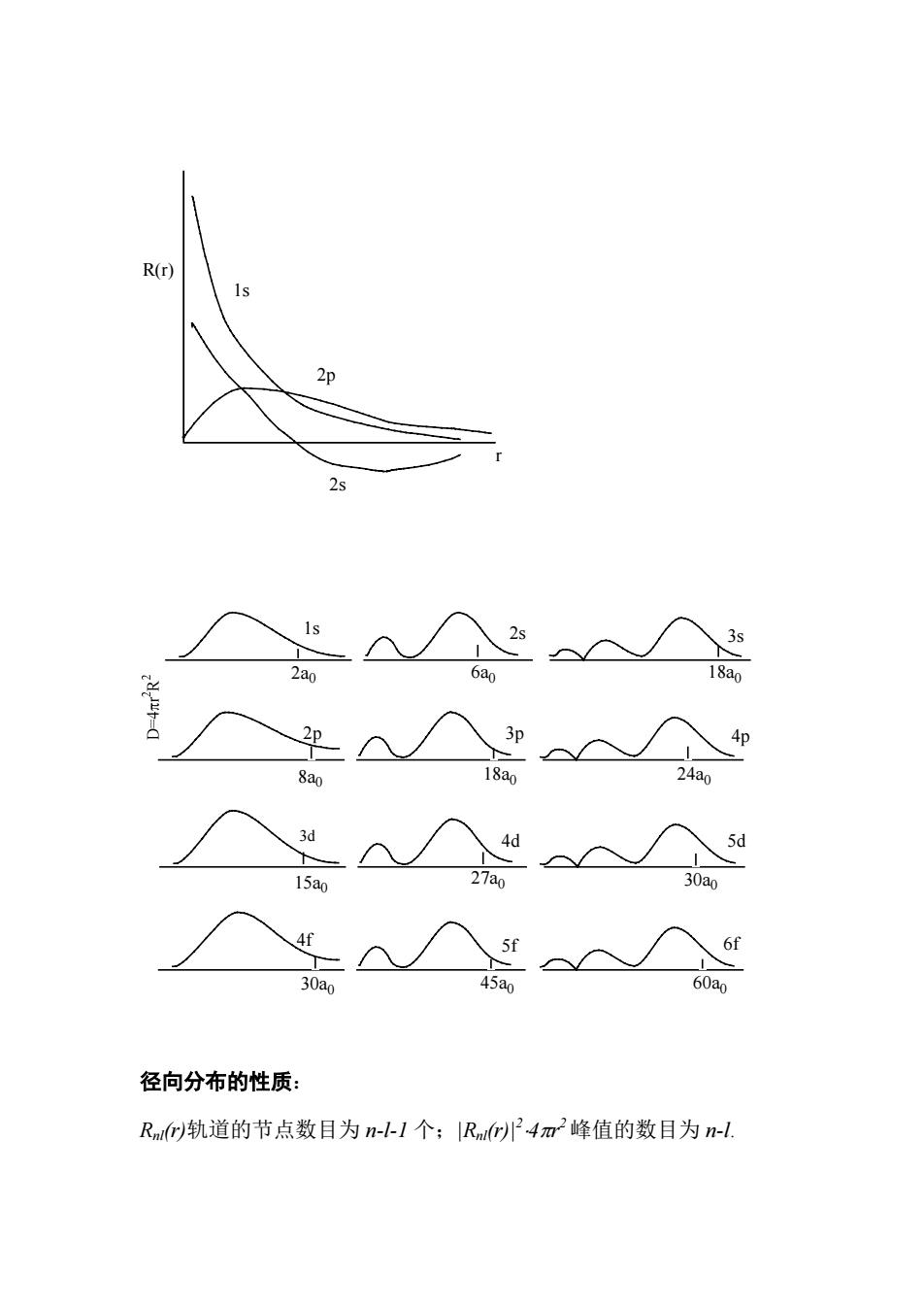
R(r 27a 径向分布的性质: Rn)轨道的节点数目为n-1个;Rn4m峰值的数目为n-l
1s 2s 2p R(r) r 1s 2s 3s 2p 3p 4p 3d 4d 5d 4f 5f 6f 2a0 6a0 18a0 8a0 18a0 24a0 15a0 27a0 30a0 30a0 45a0 60a0 径向分布的性质: Rnl(r)轨道的节点数目为 n-l-1 个;|Rnl(r)|2 ⋅4πr 2峰值的数目为 n-l
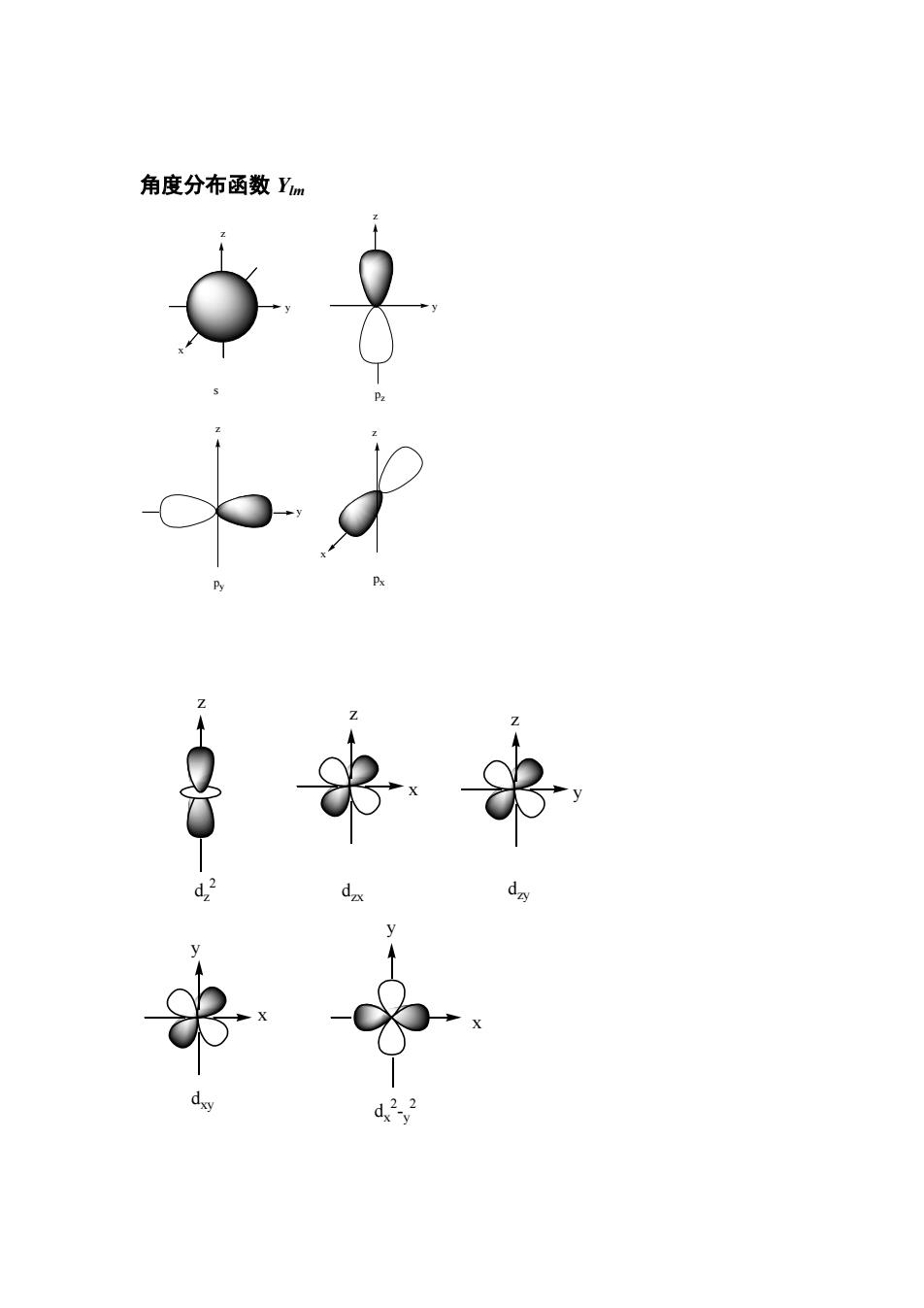
角度分布函数Ym
角度分布函数 Ylm x y z y z z y x z p px y pz s z z x z y y x y x dz 2 dzx dzy dxy dx 2 -y 2
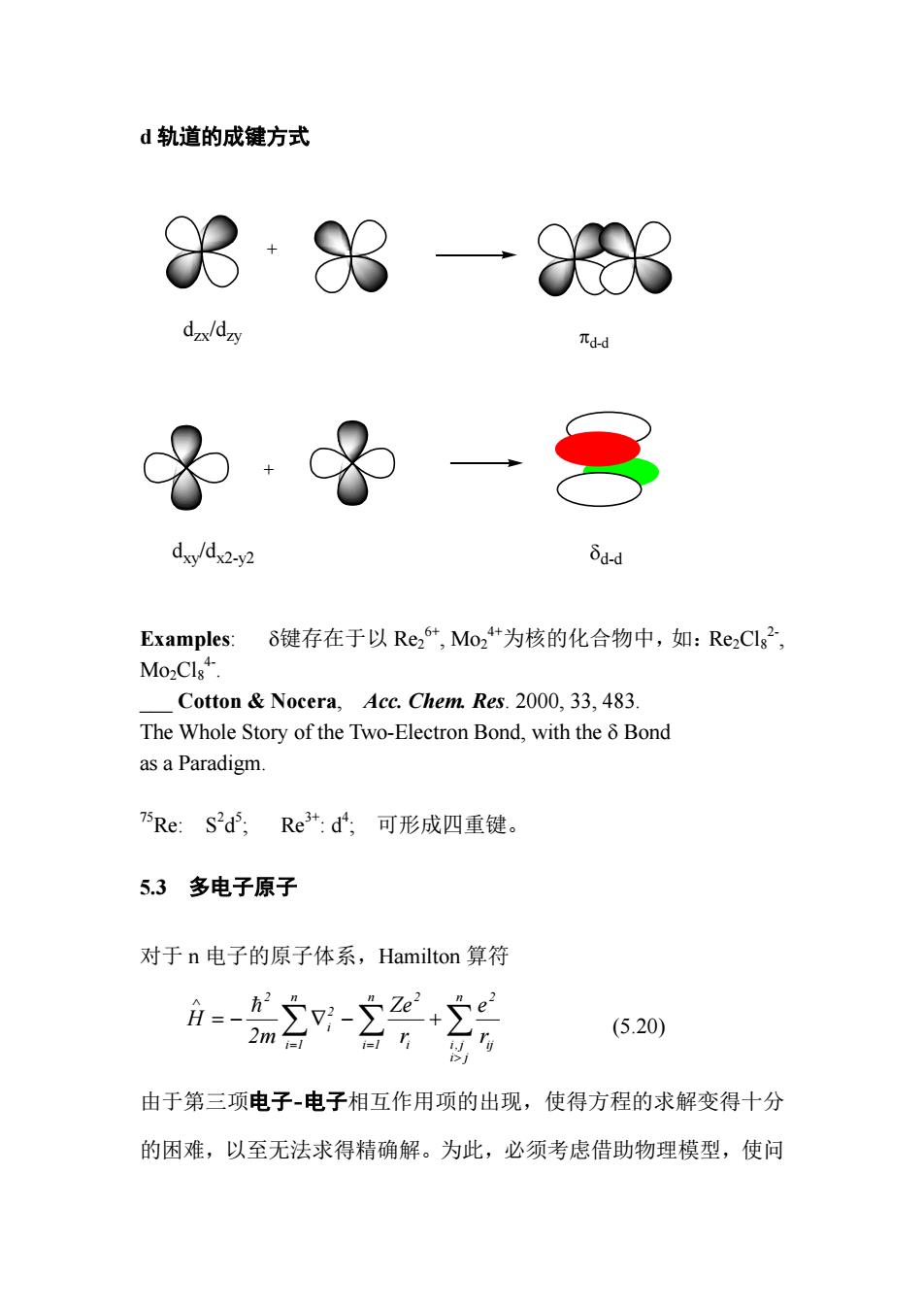
d轨道的成键方式 83·88- 883 d-x/dzv d-c dxy/dx2-y2 δa.d Examples: 8键存在于以Re26+,Mo24+为核的化合物中,如:Re2Clg2 Mo2Cls". Cotton Nocera.Acc.Chem.Res.2000.33,483. The Whole Story of the Two-Electron Bond,with the 8 Bond as a Paradigm. 5Re:S2d,Re3:d,可形成四重键。 5.3多电子原子 对于n电子的原子体系,Hamilton算符 (5.20) 由于第三项电子-电子相互作用项的出现,使得方程的求解变得十分 的困难,以至无法求得精确解。为此,必须考虑借助物理模型,使问
d 轨道的成键方式 dzx/dzy + dxy/dx2-y2 + δd-d πd-d Examples: δ键存在于以 Re2 6+, Mo2 4+为核的化合物中,如:Re2Cl8 2-, Mo2Cl8 4-. ___ Cotton & Nocera, Acc. Chem. Res. 2000, 33, 483. The Whole Story of the Two-Electron Bond, with the δ Bond as a Paradigm. 75Re: S2 d5 ; Re3+: d4 ; 可形成四重键。 5.3 多电子原子 对于 n 电子的原子体系,Hamilton 算符 ∑ ∑ ∑ > = = ∧ = − ∇ − + n i j i,j ij n 2 i 1 i n 2 i 1 2 i 2 r e r Ze 2m H = (5.20) 由于第三项电子-电子相互作用项的出现,使得方程的求解变得十分 的困难,以至无法求得精确解。为此,必须考虑借助物理模型,使问

题得到简化。 中心场模型(Central--field approximation) 先考虑某一个电子,如电子1的势能 乃和 (5.21) 式中1是电子1到核的距离,1是第i个电子与电子1之间的距 离。若近似地认为电子1所受到其它电子的排斥作用可以取一个平均 值,有 4G)=-2e2、 e2 (5.22) 上式的第二项经径向和角度方向的平均化处理,得到仅与1有关的函 数,为此,令 i In r (5.23) 代入(5.22)式,得 r)=2e+e.-亿-oe (5.24) 式中o1称为屏蔽常数,ō1的数值反映了其它n-1个电子对电子1排斥 作用的大小。将(5.24)式所示势能函数代入求解单电子1(独立电 子模型)的Schroedinger方程,得到 【Lp-Z-gew=Ew 2m (5.25)
题得到简化。 中心场模型(Central-field approximation) 先考虑某一个电子,如电子 1 的势能 ∑ ≠ = − + n i 1 i1 2 1 2 1 1 i r e r Ze V (r ,r ) (5.21) 式中 r1是电子 1 到核的距离,ri1是第 i(i≠1)个电子与电子 1 之间的距 离。若近似地认为电子 1 所受到其它电子的排斥作用可以取一个平均 值,有 ∑ ≠ = − + n i ir e r Ze V r 1 1 2 1 2 1 1 ( ) (5.22) 上式的第二项经径向和角度方向的平均化处理,得到仅与 r1有关的函 数,为此,令 1 2 1 1 1 2 r e r e n i i σ ∑ = ≠ (5.23) 代入(5.22)式,得 1 2 1 1 2 1 1 2 1 1 ( ) ( ) r Z e r e r Ze V r σ −σ = − + = − (5.24) 式中σ1称为屏蔽常数,σ1的数值反映了其它 n-1 个电子对电子 1 排斥 作用的大小。 将(5.24)式所示势能函数代入求解单电子 1(独立电 子模型)的 Schroedinger 方程,得到 ψ ψ σ E r Z e m = − − ∇ − ] ( ) 2 [ 1 2 2 1 1 1 2 = (5.25)