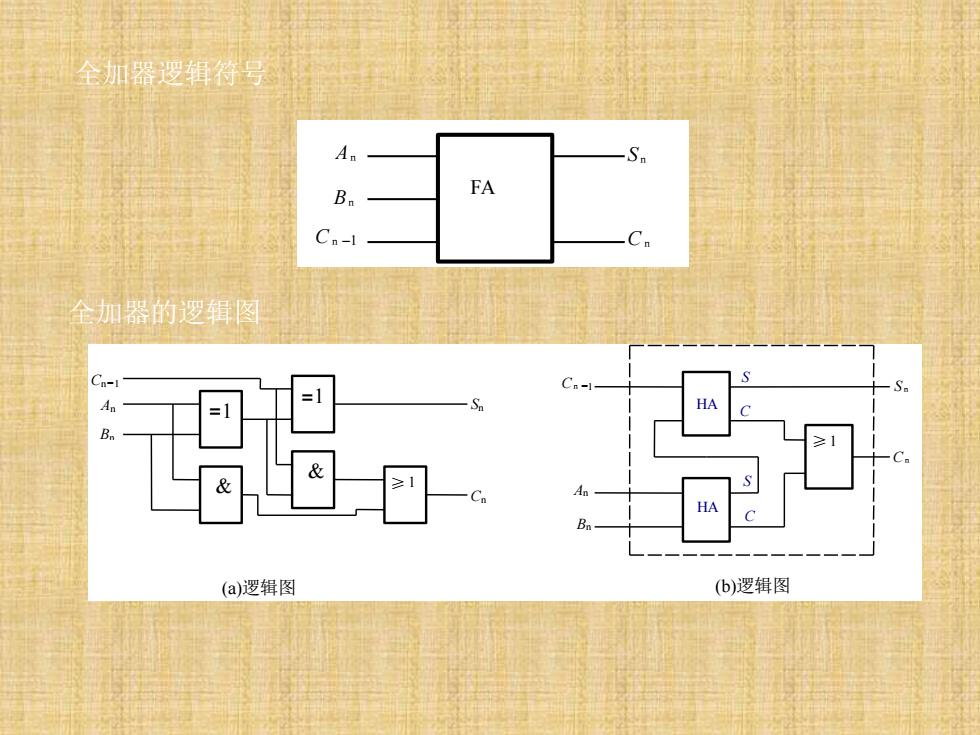
全加器逻辑符号 An Bn FA Cn-1 全加器的逻辑图 Cn-1- =1 An HA B ≥1 HA C (a)逻辑图 (b)逻辑图
Cn-1 An Sn Bn Cn FA 全加器逻辑符号 全加器的逻辑图 An Bn Cn-1 Sn Cn HA C S HA C S (a)逻辑图 (b)逻辑图 Cn-1 An Bn Sn Cn ≥ 1 =1 =1 & ≥ 1 &
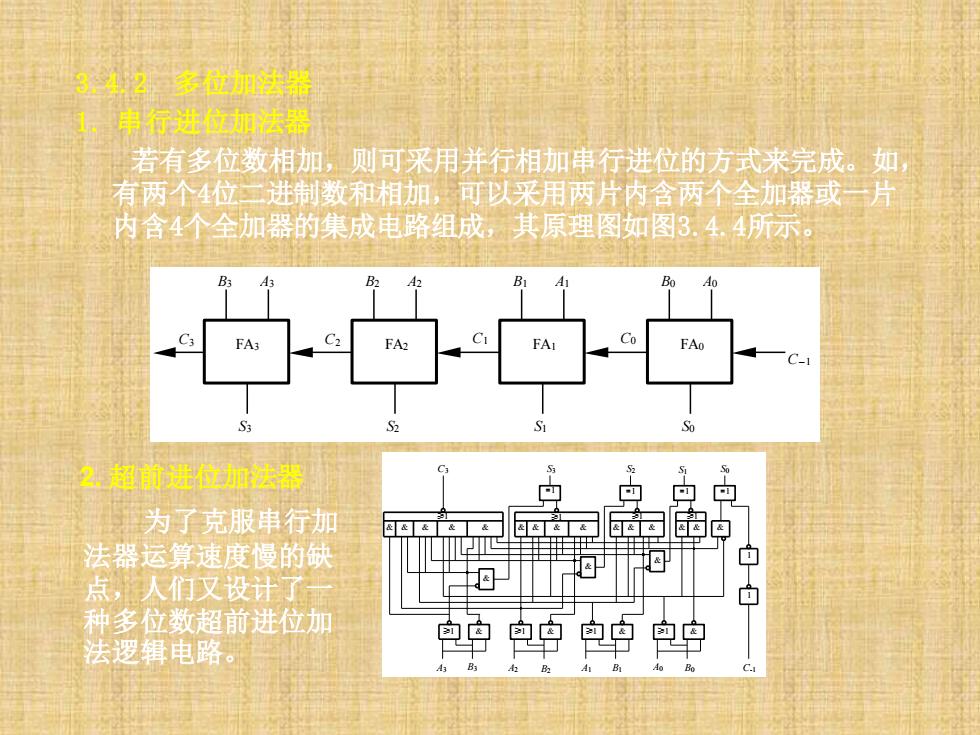
3.4,2多位加法器 1,申行进位加法器 若有多位数相加,则可采用并行相加串行进位的方式来完成。如 有两个4位二进制数和相加,可以采用两片内含两个全加器或一片 内含4个全加器的集成电路组成,其原理图如图3.4.4所示。 B3 B 9 FA Co FAo 一C- 2.超前进位加法器 由 回回 为了克服串行加 &&&& &&& 起电 法器运算速度慢的缺 丰 白 点,人们又设计了 0- 种多位数超前进位加 法逻辑电路 包中 包中包中 包中
3.4.2 多位加法器 1. 串行进位加法器 若有多位数相加,则可采用并行相加串行进位的方式来完成。如, 有两个4位二进制数和相加,可以采用两片内含两个全加器或一片 内含4个全加器的集成电路组成,其原理图如图3.4.4所示。 S0 B3 A3 B2 A2 B1 A1 B0 A0 S3 S2 S1 C-1 C3 C2 C1 C0 FA3 FA2 FA1 FA0 2. 超前进位加法器 A3 A2 A1 B1 A0 C3 S3 S2 S1 S0 B3 B2 B0 C-1 ≥1 ≥1 ≥1 ≥1 ≥1 ≥1 ≥1 ≥1 =1 =1 =1 =1 & & & & & & & & & & & & & & & & & & & & & & 1 1 为了克服串行加 法器运算速度慢的缺 点,人们又设计了一 种多位数超前进位加 法逻辑电路
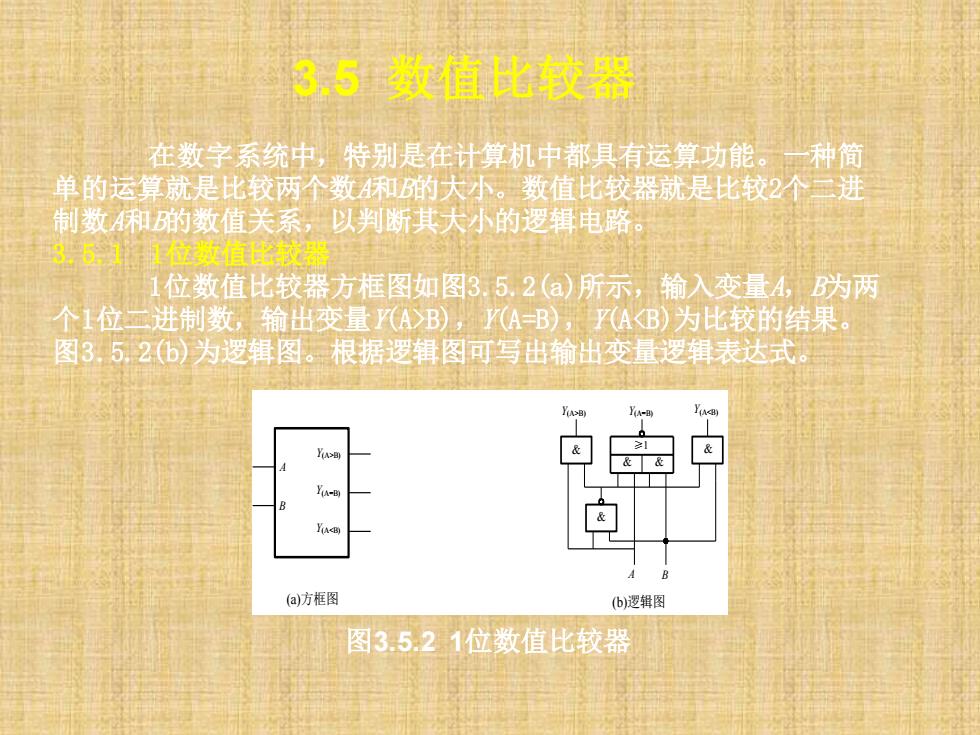
3.5数值比较器 在数字系统中,特别是在计算机中都具有运算功能。一种简 单的运算就是比较两个数和的大小。数值比较器就是比较2个三进 制数和的数值关系,以判断其大小的逻辑电路。 3,5.11位数值比较器 位数值比较器方框图如图3.5,2()所示,输入变量4,B为两 个1位二进制数,输出变量(A>B),(A=B),了AB)为比较的结果。 图3,5,2(6)为逻辑图。根据逻辑图可写出输出变量逻辑表达式 可 (a)方框图 b)逻辑图 图3.5.21位数值比较器
3.5 数值比较器 在数字系统中,特别是在计算机中都具有运算功能。一种简 单的运算就是比较两个数A和B的大小。数值比较器就是比较2个二进 制数A和B的数值关系,以判断其大小的逻辑电路。 3.5.1 1位数值比较器 1位数值比较器方框图如图3.5.2(a)所示,输入变量A,B为两 个1位二进制数,输出变量Y(A>B),Y(A=B),Y(A<B)为比较的结果。 图3.5.2(b)为逻辑图。根据逻辑图可写出输出变量逻辑表达式。 图3.5.2 1位数值比较器 Y(A>B) Y(A=B) Y(A<B) A B (a)方框图 (b)逻辑图 Y(A>B) Y(A=B) Y(A<B) A B & & & ≥1 & &
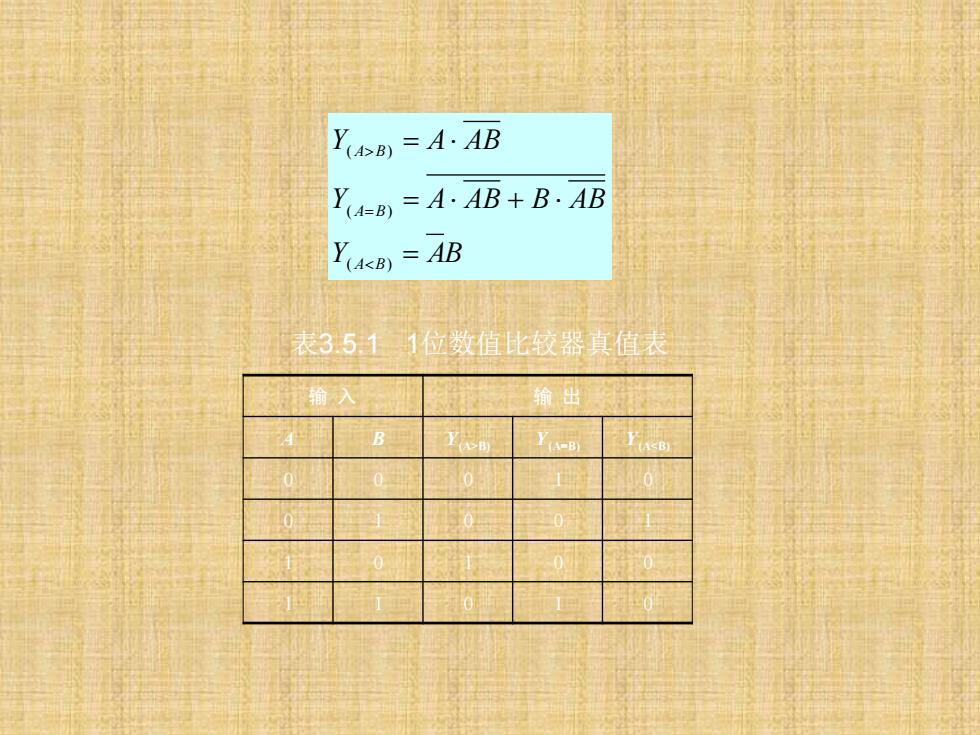
Y(AB)=A.AB Y(A-B) A·AB+B·AB Y(B)AB 表3.511位数值比较器真值表 输入 输 B Y A<B 0 0
输 入 输 出 A B Y(A>B) Y(A=B) Y(A<B) 0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 1 1 0 1 0 表3.5.1 1位数值比较器真值表 Y AB Y A AB B AB Y A AB A B A B A B = = + = = ( ) ( ) ( )

3.5.24位数值比较器 将个如图3.5.2(6)所示1位数值比较器合理连接便可得到 位数值比较器。74LS85为集成4位数值比较器,其方框图如 图3.5.3所示。 Y(A-B) Y(A=B) Y(A<B) 74LS85 I(A-B)(A=B)I(A<B)A3 A2 A1 A0 B3 B2 B1 Bo 图3.5.374LS85方框图
3.5.2 4位数值比较器 将n个如图3.5.2(b)所示1位数值比较器合理连接便可得到 n位数值比较器。74LS85为集成4位数值比较器,其方框图如 图3.5.3所示。 74LS85 Y(A>B) Y(A=B) Y(A<B) I(A>B) I(A=B) I(A<B) A3 A2 A1 A0 B3 B2 B1 B0 图3.5.3 74LS85方框图