
3.3,2组合逻辑电路的设计举例 【例33.1】已知有3个逻辑变量A,B,C,利用与非门设计一个逻辑电 路,判断3个变量中是否有多数个取值为] 解 ①定义输入变量和输出变量。A,B,C,3个变量应为输入变量,设输 出变量为Y。当Y=I时,表明AB.C多数取值为1,否则YO ②根据题意列填值表,见表331 ③根据真值表写出逻辑表达式,化简,并将其变换为“与非一与非 表达式 33.1 Y=ABC+ABC+ABC=AB+AC+BC=AB·AC·BC ④根据逻辑表达式画逻辑图,如图331所示
3.3.2 组合逻辑电路的设计举例 【例3.3.1】已知有3个逻辑变量A,B,C,利用与非门设计一个逻辑电 路,判断3个变量中是否有多数个取值为1。 解 ① 定义输入变量和输出变量。A,B,C ,3个变量应为输入变量,设输 出变量为Y。当Y=1时,表明A,B,C多数取值为1,否则Y=0。 ②根据题意列真值表,见表3.3.1。 ③ 根据真值表写出逻辑表达式,化简,并将其变换为“与非-与非” 表达式。 (3.3.1) ④ 根据逻辑表达式画逻辑图,如图3.3.1所示。 Y = ABC + ABC + ABC = AB + AC + BC = AB AC BC
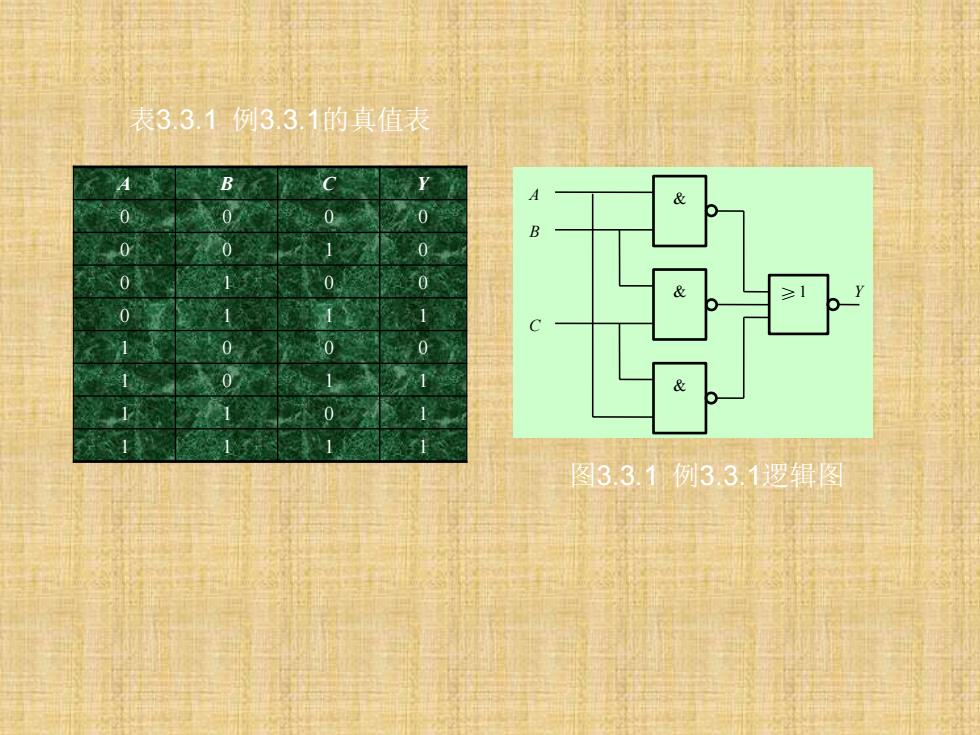
表3.3.1例3.3.1的真值表 B C 0 B 0 1 0 0 0 0 C 0 0 0 0 图33.1例33.1逻辑图
A B C Y 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 表3.3.1 例3.3.1的真值表 Y A B C ≥1 & & & 图3.3.1 例3.3.1逻辑图

3.4加法器 在数字系统中,无其是在计算机的数字系统中 盖进制加法器是宿 的基本部件之 市。 在进行两个进制数之间的算术运算时,无论是 加减、乘、除,最后都可化作加法运算来实现。能够实现加法运 算的电路称为加法器,它是算术运算的基本单元电路 3.4.1半加器和全加器 ,半加器 只考虑两个1位进制数和B相加,不考虑低位来的进位数的相 加称为半加,实现半加的电路称为半加器。半加器的真值表见表 34 表34.1半加器的真值表
3.4 加 法 器 在数字系统中,尤其是在计算机的数字系统中,二进制加法器是它 的基本部件之一。在进行两个二进制数之间的算术运算时,无论是 加、减、乘、除,最后都可化作加法运算来实现。能够实现加法运 算的电路称为加法器,它是算术运算的基本单元电路。 3.4.1 半加器和全加器 1. 半加器 只考虑两个1位二进制数A和B相加,不考虑低位来的进位数的相 加称为半加,实现半加的电路称为半加器。半加器的真值表见表 3.4.1。 输 入 输 出 A B S C 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 表3.4.1 半加器的真值表

半加器的逻辑表达式为 S=AB+AB C=A.B 加器的逻辑符号如图34,1b)所示 (a)逻辑电路 -S HA (b)逻辑符号
__ __ S A B A B C A B = + = 半加器的逻辑表达式为 半加器的逻辑符号如图3.4.1(b)所示 A S B C HA (b)逻辑符号 A B S C (a)逻辑电路 =1 &
2.全加器 除了两个1位云进制数相加以外,还与低位向本位的进位数相加,称 之为全加,所构成的电路称为全加器。全加器的真值表见表342。全 加器的逻辑符号如图3.42所示。 表342全加器的真值表表 输出 B 0
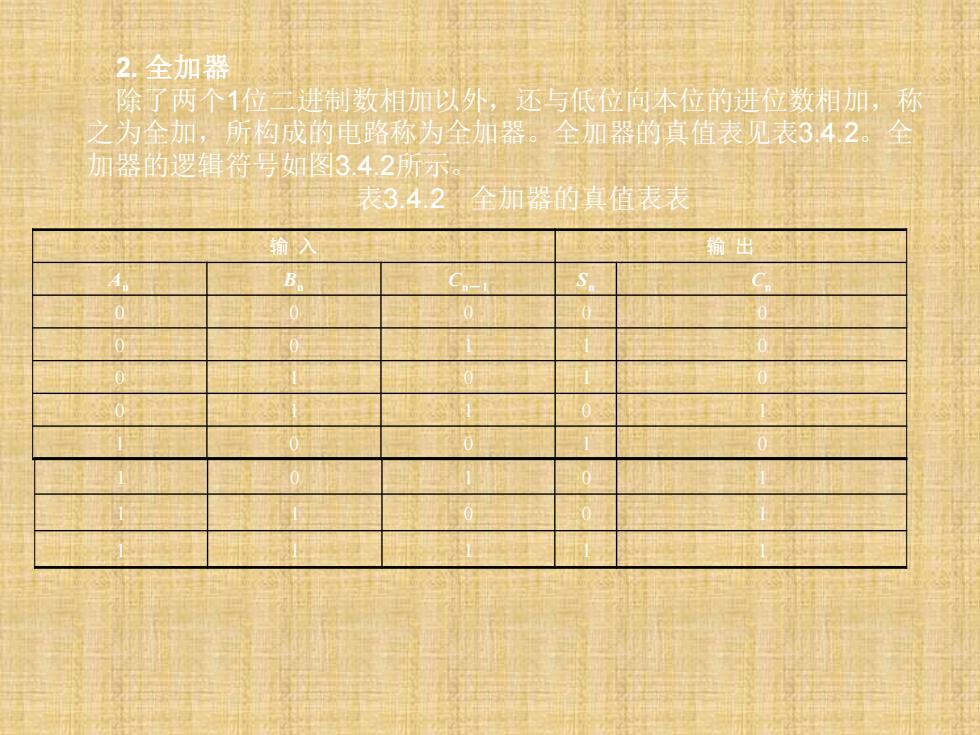
2. 全加器 除了两个1位二进制数相加以外,还与低位向本位的进位数相加,称 之为全加,所构成的电路称为全加器。全加器的真值表见表3.4.2。全 加器的逻辑符号如图3.4.2所示。 表3.4.2 全加器的真值表表 输 入 输 出 An Bn Cn-1 Sn Cn 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1