
付,其光的强度最大:I=4I。当P点满足 sin0:20合n=0,2 (1-3) 时,其光的强度为零, 虽然光的波动性有大量的实验事实和光的电磁理论的支持, 但本世纪初所发现的黑体辐射、光电效应等现象却揭示了只把光 看作波动的严重局限性。 黑体辐射问题所研究的是辐射与周围物体处于平衡状态时的 能量按波长(或频率)的分布。所有物体都发射出热辐射,这种 辐射是一定波长范围内的电磁波。对于外来的辐射,物体有反射 和吸收的作用。如果一个物体能全部吸收投射其上的辐射而无反 射,这种物体就称为绝对黑体,简称黑体。一个空腔可近似地看 作黑体。当空腔与内部的辐射处于平衡时,腔壁单位面积所发射 出的辐射能量和它所吸收的辐射能量相等。实验得出的平衡时辐 射能量密度按波长分布的曲线,其形状和位置只与黑体的绝对温 度有关,而与黑体的形状及组成的物质无关。许多物理学家曾试 图用经典物理学来解释这种能量分布的规律,推导与实验符合的 能量分布公式,但都未获得成功. 1896年,维恩(Wien)根据能谱实验数据,并由热力学关 系和一些假设提出如下能量分布的经验公式 p(v,T)dv=cv'e-2"/dv (1-4) 式中c1和c,为常数,v为频率,T为绝对温度.(1-4)式 只在高频下才与实验相符合, 1900年,瑞利(Rayleigh)在金斯(Jeans)的帮助下,根 据经典电动力学推导出空腔的单位体积内辐射频率在)到v+) 之间的振动方式数目是8山。每种振动方式总是包括两种能量 :能项界芗能项,因此按照经典统计的能量均分定理,每一 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

振动方式的能量是T,‘由此得到黑体辐射能量分布的公式为 o,7d-8a7d山 (1-5) 式中c是光速,是玻尔兹曼(Boltzmann)常数.(1-5)式只 在低频下与实验符合。而且由上式讨算总能量密度,即对所有频 率积分,由于高频的贡献,其结果是发散的,这在历史上称为紫 外灾难(ultraviolet catastrophe),这样,经典理论在解释 黑体辐射现象上遇到了严重困难,这些困难是由普朗克(Planck: 在1900年提出“量子”的概念后才得到解决的, 1.1.2量子概念的提出 Planck把黑体看作是由带电的者振子所组成,并假定这些 谐振子的能量不能连续变化,而只能量子化地取一些分立值,即 振子的能量只能取 、E。=nk。 (1-6) 式中∈。为最小能量,”为正整数.由经典统计理论,振子能量 为E.=nE。的几率与eeur成正比,于是振子的平均能量是 ∑E,e-nEc/kT(。∑ner ”= #座0 (1-7) ∑er e-lar 0 1=0 令x=e∈/r,利用展开式 k 则(1-7)式的分母为(1-e6").再令y=∈,/kT,利 用公式 4 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播
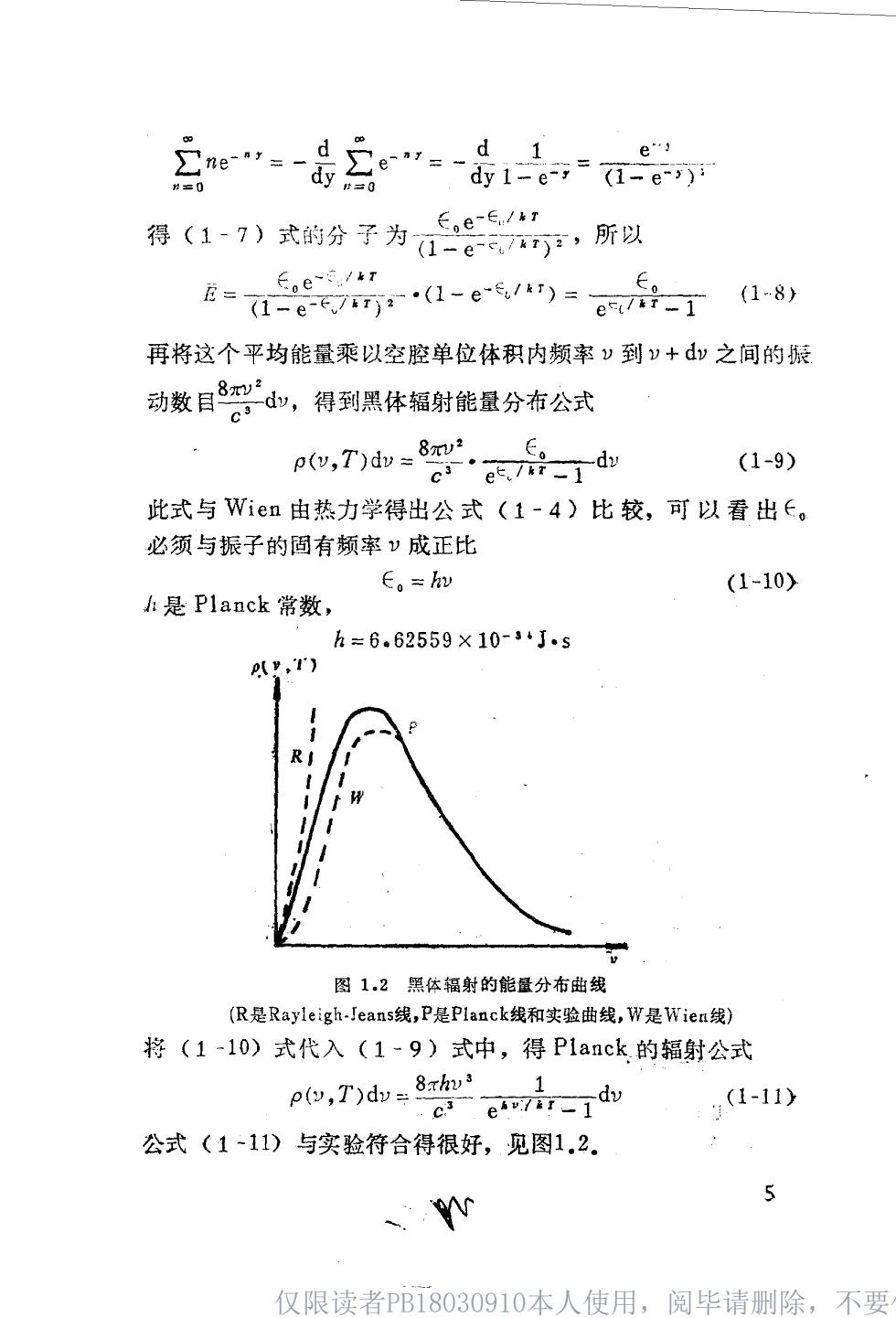
,∈0e∈/r 得(17)式的分子为ā8,所以 E=ag71-e6)=e7-T1-8) 再将这个平均能量乘以空腔单位体积内频率”到)+dv之间的振 动数日8。,得到黑体韬射能最分右公式 p(y,T)dw=8w.6。 c‘e7i-】dw (1-9) 此式与Wien由热力学得出公式(1-4)比较,可以看出E。 必须与振子的固有频率”成正比 E。=h (1-10> h是Planck常数, h=6.62559×10-·J.s 图1,2黑体辐射的能量分布曲线 (R是Rayleigh-Jeanss线,P是Planck线和实验曲线,W是Wier线) 将(1-10)式代入(1-9)式中,得P1anck的辐射公式 pe,7山=8e71如 ,(1-11) 公式(1-11)与实验符合得很好,见图1.2. 5 、W 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

当频率很高时,即/T>1,则(1-11)式分母中的1可 以略去,于是得到 p,d 这就是Wien公式(1-4). 当频率很低时,即hv/T《1,可利用展开式 e*/ar=1+h/kT+. 取前两项,(1-11).式变为 ,dvT 这就是Rayleigh-Jeans公式(1-5), Planck能量量子化的假设如此成功地解释了黑体辐射现 象,使人们不得不来重新探讨辐射的本性。尽管辐射的波动本性 为一系列实验事实所证实,例如前面讨论的光(辐射)的双缝衍 射实验,但是按照Planck的假设,在辐射过程中所发射和吸收 的能量单位却是量子化的能量子加.那么可否设想量子如具有 粒子的某些性质呢?这一问题留待下一节讨论.· 1.2辐射的粒子性 首先肯定光除了波动性之外还有粒子性的是爱因斯坦(E血 stein)·他认为电磁辐射不仅在被发射和吸收时以能量为hw的 粒子形式出现,而且以这种形式在空间以速度c运动。这种粒子 叫作光量子或光子,用这个观点,Einstein成功地解释了光电 效应. 1.2.1光电效应 光电效应是当光照射到金属上时,有电子从金属表面逸出。 这种电子称为光电子.,实验表明,只有当光的频率大于某一阈值 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

时,才有光电子发射出来,如果光的频率低于这个阈值,则无论 光的强度多大、照射时间多长,都没有光电子产生;光的频率越 高,光电子的能量就越大;光的强度只影响光电子的数目,而与 光电子的能量无关。光电效应的这些规律是经典理论所无法解释 的。按照光的电磁理论,光的能量只决定于光的强度,·而与光的 频率无关. 按照Einstein的光子学说,当光照射到金属表面时,能量 为)的光子被电子所吸收。电子把这能量的一部分用作为它脱 出金属表面所消耗的功W。(称为脱出功),另一部分就是电子离 开金属后的动能24,即 o=加- (1-12) 如果电子所吸收的光子能量y小于W。,则电子不能脱出金属表 面,因而没有光电子产生。光的频率决定光子的能量,光的强度 只决定光子的数目,光子多,产生的光电子也多。这样,经典理 论所不能解释的光电效应就得到了圆满的说明。 光子不但具有能量,而且具有动量。按照相对论关系式,以 速度v运动的粒子,其能量为 E=P.c/V1-070 式中:4。为粒子的静止质量。对于光子,口=c、光子的能量总 是有限的,所以由上式得到光子的静止质量为零。由相对论中能 量和动量的关系式 E?=μc*+c2P2 可得到光子的能量E和动量P的关系是E=cP,由光子的能量 E=hv (1-13) 可得到光子的动量为 P=h/2 (1-14) 按照Einstein的光子学说,光是一束以光速c行进的光子 7 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播