
9.8.5石墨型(A,型).(490) 9,8.6NaC1型. (490) 9.8.7CsC1型.(491) 9.8.8闪锌矿型(立方ZnS型). (491) 9.8.9纤锌矿型(六方ZnS型). (491) 9.8.10红镍矿(NiAs)型 (492) 9.8.11萤石(CaF.)型 (492) 9.8,12金红石(Ti02)型. (493) 9.9晶体衍射的一般介绍.(494) 9.9.1X射线衍射.(494) 9.9.2电子衍射和中子衍射.(495) 9.10X射线行射方程. (495) 9,10.1劳厄(Laue)方程.(496) 9.10.2布拉格(Bragg)方程. (498) 9.11衍射强度与原子的分布.(501) 9.11.1原子的散射因子. (501) 9.11.2几何结构因子. (503) 9.11.3电子密度p与结构因子F.:关系的推导.(507) 9.12晶体的X射线衍射图及其克用.(509) 9.12.1L8ue法.(509) 9.12,2回转法. (510) 9.12,3粉末法. (511) 9.13固体样品的物相分析.(516) 9.13.1粉末衍射卡片.(516) 9.13.2物相定性分析.(518) 习题 (522) 第十章固体的电子结构 10.1晶体的键型.(525) 10.1.1共价键.(525) xiii 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

101.2离子键. (525) 10,1.3金属键. (529) 10.1.4氢键. ., (530) l0.1.5范德瓦尔斯(van der Waals)力. (531) 10.1.6混合键.(532) 10.2原子的各种半径. (532) 10.2.】共价半径. (533) 10.2.2离子半径· (534) 10.2.3金属的原子半径. (536) 10.2.4 van der Waals半径.(536) 10,3固体能带的定性描述.(537) 10.3.1紧束缚近似. (537) 10.3.2近自由电子近似: (540) 10.4金属中的电子气.(544) 10.4.1势箱中的自由电子.(544) 10.4.2周期性边界条件下的电子气.(545) 10.5电子气的费密(Fermi)能量.(549) 10.5.1电子气的能量分布 (549) 10.5.2 Fermi能量的计算 .(550) 10.5.3 Fermi面.(553) 10.6金属中电子气的热容量.(554) 10.6.1电子的平均能量(554) 10.6.2电子气的热容量. (554) 10.7布洛赫(B1och)波和倒格子.(555) 10.7.1B10ch波.(555) 10.7.2.倒格子.(558) 10.8克龙尼克-潘纳(Kronig-Penney).势.(562) 10.8,1 Kronig-Penney势场中的Scbrodinger方程(562) l0.&,&Kronig-Penney势场中Schrodinger方程 xiv 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

的解.(563) 10.9周期场中电子的微扰法处狸. (568) 10,9.1非简并的情况. (568) 10.9.2简并的情况. (571) 10.10晶体中电子的速度和加速度.(576) 10.10.1电子的速度. .(576) 10.10.2电子的加速度和有效质量.(578) 10.11金属、半导体和绝缘体.(580) 10.11,1导体和绝缘体的能带.(581) 10.11.2半导体的能带 .(585) 10.11.3空穴.(586) 10.12三维情况的B10ch定理. (587) 10.12.1理想晶体的单电子波函数.(588) 10.12.2布里渊(Brillouin)区 (590) 10.13紧束缚近似一LCA0法计算能带.(594) 10.13.1模型与微扰计算.(594) 10.13.2实例.(598) 10.14原子簇的量子化学计算. (599) 10.14.1原子簇模型的选取.(599) 10.14.2顶势法.(601) 10.14.3Xc方法.(601) 习题. (603) “习题答案和提示 附录 。化学上重要对称群的特征标表.(615) 2.0,群的相关表. (631) 3。不可约表示的直积. (632) 4。常用的物理常数 .(633) 5。能量转换因子.(634) 参考文献 xvi 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

第一章量子力学基础 1.1量子概念的提出 人们生活在宏观世界中,对微观世界的认识往往总是下意识 地照搬在宏观世界中所积累的知识和经验。但每当人们试图用 经典物理学来描述微观粒子(泛指原子、分子、原子核、电子等 实物微粒)的运动规律时,总会得到与实验有明显矛盾的结论. 最明显的例子,是把通常的电动力学用于龟子绕原子核作经典轨 道运动的原子模型(Ruther ford原子模型),当电子作这种运 动的时候,它和带电粒子的任何加速运动一样,总会不断地辐射 电磁波。由于这种辐射,电子便会不断地丧失能量,而最终落入 原子核中,故按经典电动力学理论,原子将是不稳定的,但这显 然与事实完全不符.理论和实验之间如此深刻的矛盾,表明要建 立一种适用于描述微观粒子运动规律的理论,需要根本改变基本 的物理概念和定律.这显然不是一件容易的事. 让我们先从光的本性说起。 1.1.1光的波动性与黑体辐射 光具有波动性。光的干涉、衍射和偏振现象以及光的电磁理 论从实验和理论两方面充分肯定了光的波动性。显示光的波动性 的典型实验之一是双缝衍射实验,如图1.1所示.图中A和B是 垂直于纸面的屏,A屏上有两条平行狭缝S:和S2,缝间距为 d,且d《D.同一光源S发出的光经双缝在B屏上产生衍射图 样.以E:和E:分别表示经狭缝S:和S:到达P点的光波振 动,则 1 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播
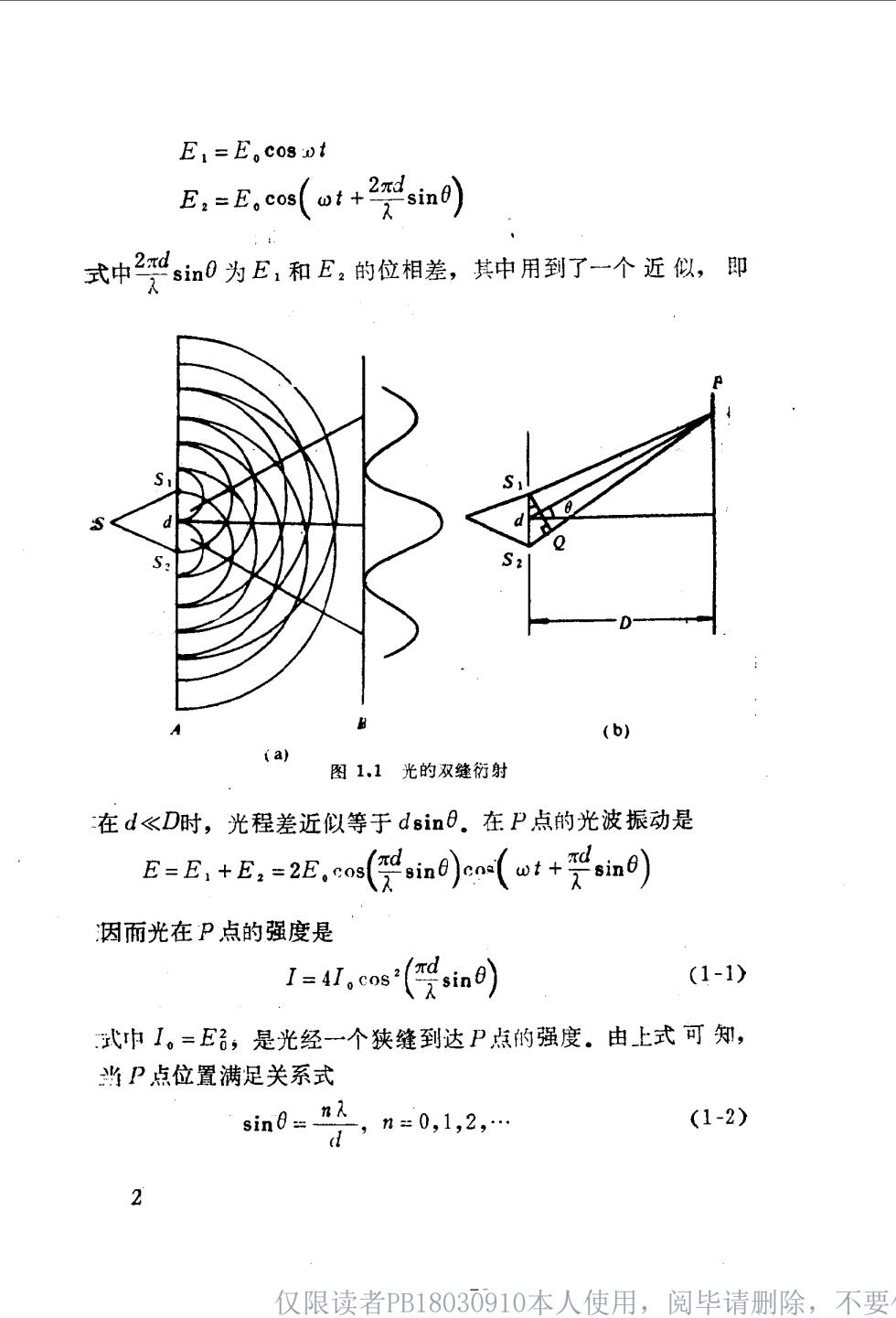
E1=E。co3Dt E:=E,cos(uf+2sin0) 式中贸0为E,和E,的位相差,其中用到了-个近以,即 (b) (a) 图1.1光的双缝衍射 在d<D时,光程差近似等于dsin日.在P点的光波振动是 E=E,+E,=2E,cos(in0)en(wt+sinf) 因而光在P点的强度是 1=4l.cos(gin0) (1-1) 式巾1,=E,是光经一个狭缝到达P点的强度.由上式可, 当P点位置满足关系式 sin0=n入 ,n=0,1,2,. (1-2) 仅限读者PB1803O910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播