
第七讲§2一1投影法的基本知识 §2一2三视图的形成与投影规律 课题:1、投影法的基本知识 2、三视图的形成与投影规律 课堂类型:讲授 教学目的:1、介绍投影法的概念、种类、应用 2、讲解正投影法的基本性质 3、介绍三投影面体系和三视图的形成、投影规律 教学要求:1、掌握正投影法的基本性质 2、理解并掌握三视图的形成和投影规律 教学重点:1、正投影法的基本性质 2、三视图的投影规律 教学难点:三视图与物体方位的对应关系 教具:自制的三投影面体系模型、简单几何体模型 教学方法:讲授与课堂演示、举例相结合。 教学过程: 一、复习旧课 简要复习平面图形的作图方法和步骤。 二、引入新课题 在工程技术中,人们常用到各种图样,如机械图样、建筑图样等。这些图样都是按照不同的 投影方法绘制出来的,而机械图样是用正投影法绘制的, 三、教学内容 (一)投影法的基本知识 1、投影法的概念 举例:在日常生活中,人们看到太阳光或灯光照射物体时,在地面或墙壁上出现物体的 影子,这就是一种投影现象。我们把光线称为投射线(或叫投影线),地面或墙壁称为投影面,影子 称为物体在投影面上的投影。 下面进一步从几何观点来分析投影的形成。设空间有一定点S和任一点A,以及不通过点S 和点A的平面P,如图2-1所示,从点S经过点A作直线SA,直线SA必然与平面P相交于
第七讲 §2—1 投影法的基本知识 §2—2 三视图的形成与投影规律 课 题:1、投影法的基本知识 2、三视图的形成与投影规律 课堂类型:讲授 教学目的:1、介绍投影法的概念、种类、应用 2、讲解正投影法的基本性质 3、介绍三投影面体系和三视图的形成、投影规律 教学要求:1、掌握正投影法的基本性质 2、理解并掌握三视图的形成和投影规律 教学重点:1、正投影法的基本性质 2、三视图的投影规律 教学难点:三视图与物体方位的对应关系 教 具:自制的三投影面体系模型、简单几何体模型 教学方法:讲授与课堂演示、举例相结合。 教学过程: 一、复习旧课 简要复习平面图形的作图方法和步骤。 二、引入新课题 在工程技术中,人们常用到各种图样,如机械图样、建筑图样等。这些图样都是按照不同的 投影方法绘制出来的,而机械图样是用正投影法绘制的。 三、教学内容 (一)投影法的基本知识 1、投影法的概念 举例:在日常生活中,人们看到太阳光或灯光照射物体时,在地面或墙壁上出现物体的 影子,这就是一种投影现象。我们把光线称为投射线(或叫投影线),地面或墙壁称为投影面,影子 称为物体在投影面上的投影。 下面进一步从几何观点来分析投影的形成。设空间有一定点 S 和任一点 A,以及不通过点 S 和点 A 的平面 P,如图 2-1 所示,从点 S 经过点 A 作直线 SA,直线 SA 必然与平面 P 相交于一
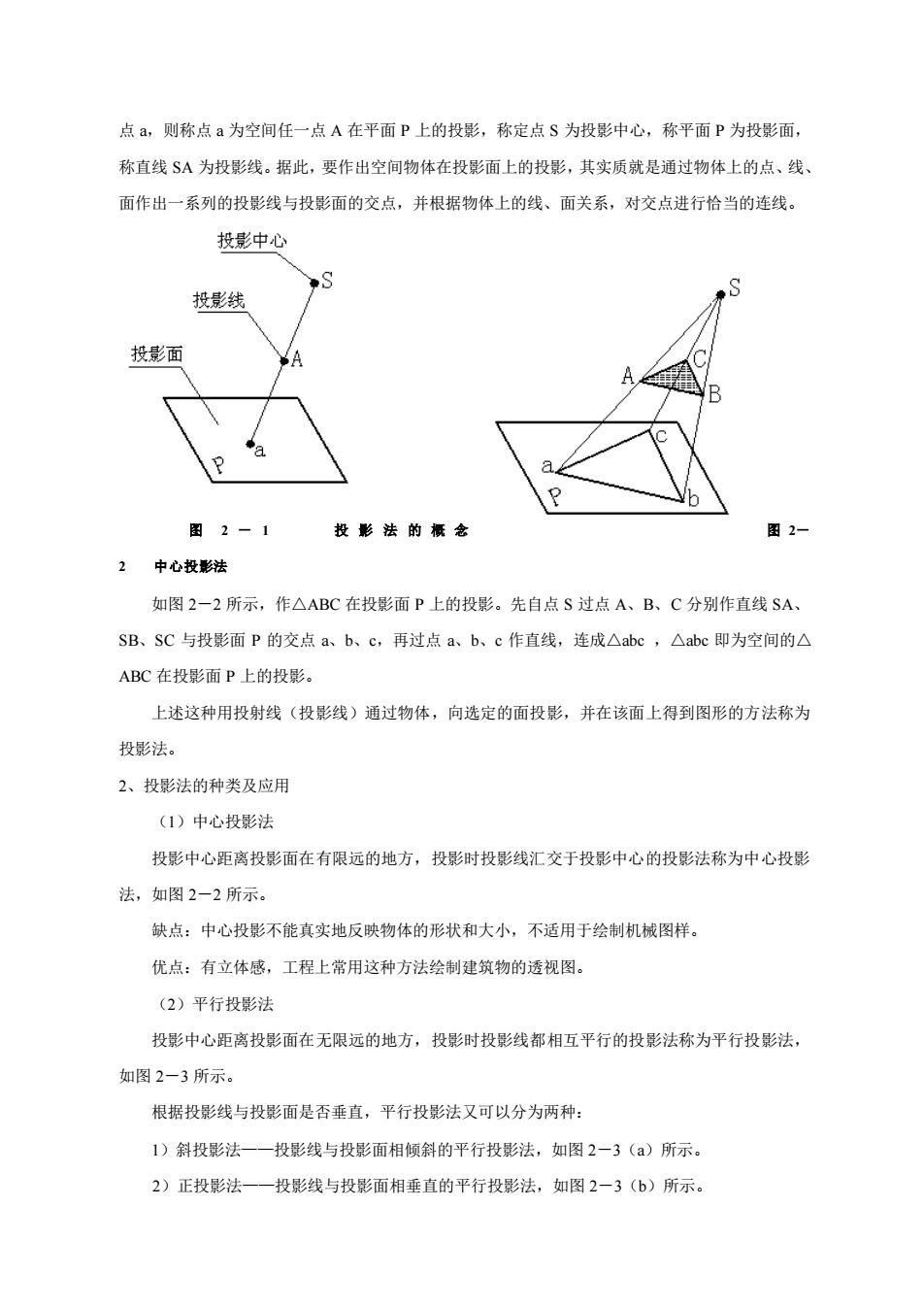
点a,则称点a为空间任一点A在平面P上的投影,称定点S为投影中心,称平面P为投影面, 称直线SA为投影线。据此,要作出空间物体在投影面上的投影,其实质就是通过物体上的点、线、 面作出一系列的投影线与投影面的交点,并根据物体上的线、面关系,对交点进行恰当的连线。 投影中心 投影线 投影 图2-1 投影法的振老 2中心投影法 如图2-2所示,作△ABC在投影面P上的投影。先自点S过点A、B、C分别作直线SA SB、SC与投影面P的交点a、b、c,再过点a、b、c作直线,连成△abc,△abc即为空间的△ ABC在投影面P上的投影。 上述这种用投射线(投影线)通过物体,向选定的面投影,并在该面上得到图形的方法称为 投影法。 2、投影法的种类及应用 (1)中心投影法 投影中心距离投影面在有限远的地方,投影时投影线汇交于投影中心的投影法称为中心投影 法,如图2-2所示。 缺点:中心投影不能真实地反映物体的形状和大小,不适用于绘制机械图样。 优点:有立体感,工程上常用这种方法绘制建筑物的透视图。 (2)平行投影法 投影中心距离投影面在无限远的地方,投影时投影线都相互平行的投影法称为平行投影法, 如图2-3所示。 根据投影线与投影面是否垂直,平行投影法又可以分为两种: 1)斜投影法一—投影线与投影面相倾斜的平行投影法,如图2一3()所示 2)正投影法一一投影线与投影面相垂直的平行投影法,如图2一3(b)所示
点 a,则称点 a 为空间任一点 A 在平面 P 上的投影,称定点 S 为投影中心,称平面 P 为投影面, 称直线 SA 为投影线。据此,要作出空间物体在投影面上的投影,其实质就是通过物体上的点、线、 面作出一系列的投影线与投影面的交点,并根据物体上的线、面关系,对交点进行恰当的连线。 图 2 - 1 投 影 法 的 概 念 图 2- 2 中心投影法 如图 2-2 所示,作△ABC 在投影面 P 上的投影。先自点 S 过点 A、B、C 分别作直线 SA、 SB、SC 与投影面 P 的交点 a、b、c,再过点 a、b、c 作直线,连成△abc ,△abc 即为空间的△ ABC 在投影面 P 上的投影。 上述这种用投射线(投影线)通过物体,向选定的面投影,并在该面上得到图形的方法称为 投影法。 2、投影法的种类及应用 (1)中心投影法 投影中心距离投影面在有限远的地方,投影时投影线汇交于投影中心的投影法称为中心投影 法,如图 2-2 所示。 缺点:中心投影不能真实地反映物体的形状和大小,不适用于绘制机械图样。 优点:有立体感,工程上常用这种方法绘制建筑物的透视图。 (2)平行投影法 投影中心距离投影面在无限远的地方,投影时投影线都相互平行的投影法称为平行投影法, 如图 2-3 所示。 根据投影线与投影面是否垂直,平行投影法又可以分为两种: 1)斜投影法——投影线与投影面相倾斜的平行投影法,如图 2-3(a)所示。 2)正投影法——投影线与投影面相垂直的平行投影法,如图 2-3(b)所示
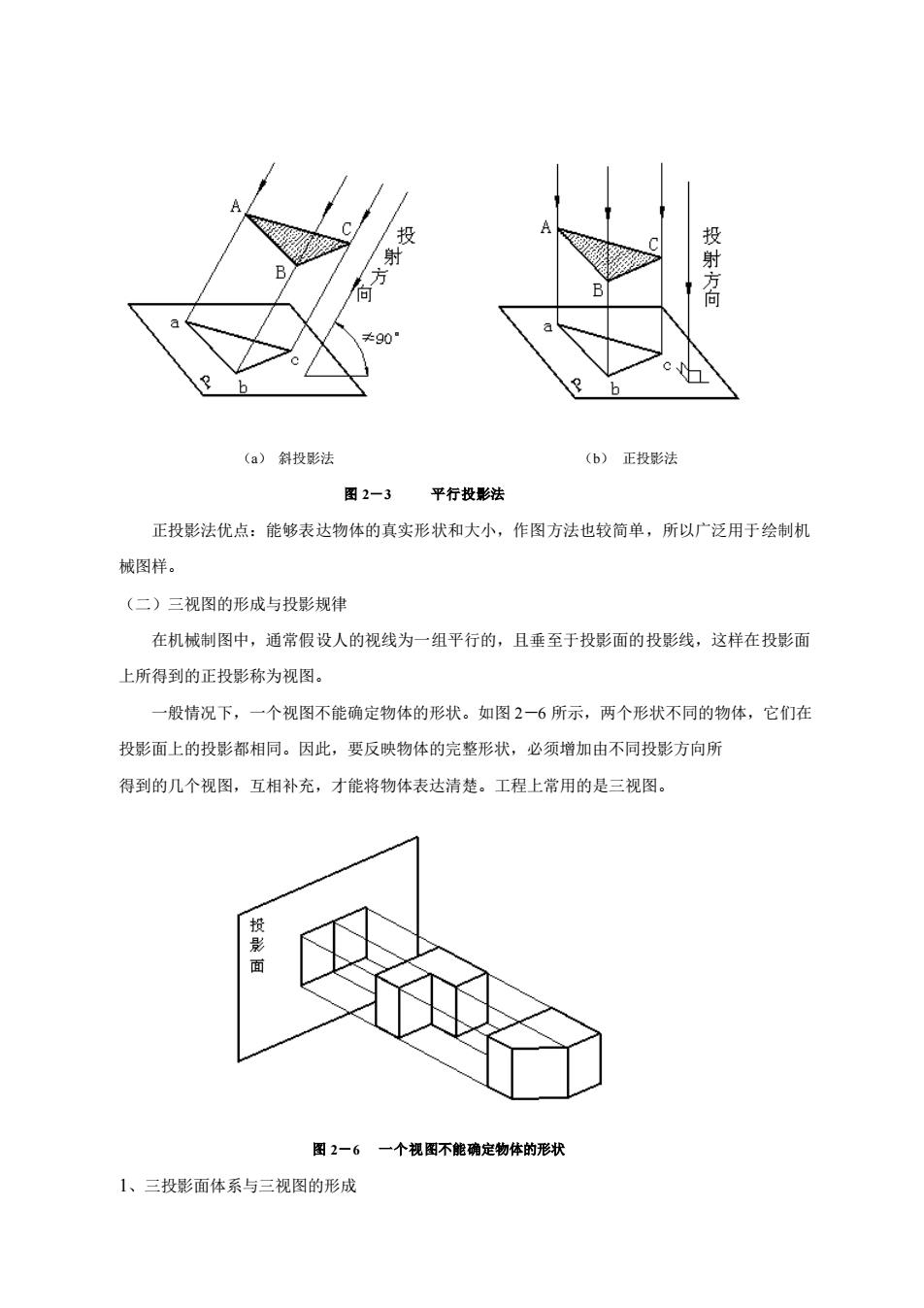
投 (a)斜投影法 (b)正投影法 图2一3平行投影法 正投影法优点:能够表达物体的真实形状和大小,作图方法也较简单,所以广泛用于绘制机 械图样。 (二)三视图的形成与投影规律 在机械制图中,通常假设人的视线为一组平行的,且垂至于投影面的投影线,这样在投影面 上所得到的正投影称为视图。 一般情况下,一个视图不能确定物体的形状。如图2一6所示,两个形状不同的物体,它们在 投影面上的投影都相同。因此,要反映物体的完整形状,必须增加由不同投影方向所 得到的几个视图,互相补充,才能将物体表达清楚。工程上常用的是三视图。 图2-6 一个视图不能确定物体的形状 1、三投影面体系与三视图的形成
(a) 斜投影法 (b) 正投影法 图 2-3 平行投影法 正投影法优点:能够表达物体的真实形状和大小,作图方法也较简单,所以广泛用于绘制机 械图样。 (二)三视图的形成与投影规律 在机械制图中,通常假设人的视线为一组平行的,且垂至于投影面的投影线,这样在投影面 上所得到的正投影称为视图。 一般情况下,一个视图不能确定物体的形状。如图 2-6 所示,两个形状不同的物体,它们在 投影面上的投影都相同。因此,要反映物体的完整形状,必须增加由不同投影方向所 得到的几个视图,互相补充,才能将物体表达清楚。工程上常用的是三视图。 图 2-6 一个视图不能确定物体的形状 1、三投影面体系与三视图的形成
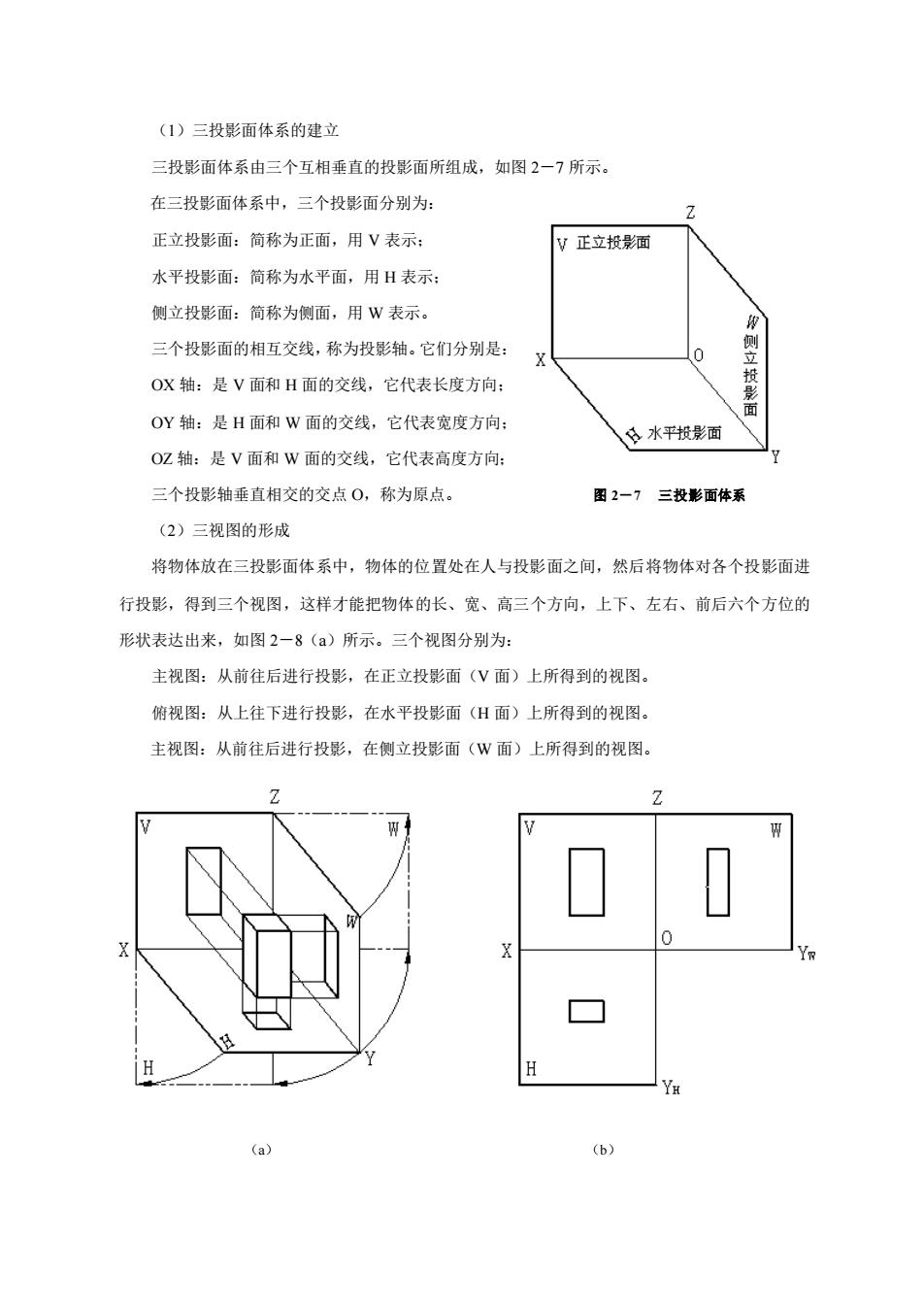
(1)三投影面体系的建立 三投影面体系由三个互相垂直的投影面所组成,如图2一7所示。 在三投影面体系中,三个投影面分别为: 正立投影面:简称为正面,用V表示: V正立投影面 水平投影面:简称为水平面,用H表示: 侧立投影面:简称为侧面,用W表示。 三个投影面的相互交线,称为投影轴。它们分别是 OX轴:是V面和H面的交线,它代表长度方向: OY轴:是H面和W面的交线,它代表宽度方向 令水平投影面 OZ轴:是V面和W面的交线,它代表高度方向: 三个投影轴垂直相交的交点O,称为原点。 图27三投影面体系 (2)三视图的形成 将物体放在三投影面体系中,物体的位置处在人与投影面之间,然后将物体对各个投影面进 行投影,得到三个视图,这样才能把物体的长、宽、高三个方向,上下、左右、前后六个方位的 形状表达出来,如图2-8(a)所示。三个视图分别为: 主视图:从前往后进行投影,在正立投影面(V面)上所得到的视图。 俯视图:从上往下进行投影,在水平投影面(H面)上所得到的视图。 主视图:从前往后进行投影,在侧立投影面(W面)上所得到的视图 a
(1)三投影面体系的建立 三投影面体系由三个互相垂直的投影面所组成,如图 2-7 所示。 在三投影面体系中,三个投影面分别为: 正立投影面:简称为正面,用 V 表示; 水平投影面:简称为水平面,用 H 表示; 侧立投影面:简称为侧面,用 W 表示。 三个投影面的相互交线,称为投影轴。它们分别是: OX 轴:是 V 面和 H 面的交线,它代表长度方向; OY 轴:是 H 面和 W 面的交线,它代表宽度方向; OZ 轴:是 V 面和 W 面的交线,它代表高度方向; 三个投影轴垂直相交的交点 O,称为原点。 图 2-7 三投影面体系 (2)三视图的形成 将物体放在三投影面体系中,物体的位置处在人与投影面之间,然后将物体对各个投影面进 行投影,得到三个视图,这样才能把物体的长、宽、高三个方向,上下、左右、前后六个方位的 形状表达出来,如图 2-8(a)所示。三个视图分别为: 主视图:从前往后进行投影,在正立投影面(V 面)上所得到的视图。 俯视图:从上往下进行投影,在水平投影面(H 面)上所得到的视图。 主视图:从前往后进行投影,在侧立投影面(W 面)上所得到的视图。 (a) (b)

图2一8三视国的形成通展开 (3)三投影面体系的展开 在实际作图中,为了画图方便,需要将三个投影面在一个平面(纸面)上表示出来,规定: 使V面不动,H面饶OX轴向下旋转90°与V面重合,W面绕OZ轴向右旋转90°与V面重合, 这样就得到了在同一平面上的三视图,如图2一8(b)所示。可以看出,俯视图在主视图的下方。 左视图在主视图的右方。在这里应特别注意的是:同一条OY轴旋转后出现了两个位置,因为OY 是H面和W面的交线,也就是两投影面的共有线,所以OY轴随者H面旋转到OYH的位置,同 时又随者W面旋转到OYw的位置。为了作图简便,投影图中不必画出投影面的边框,如图2一8 (c)所示。由于画三视图时主要依据投影规律,所以投影轴也可以进一步省略,如图2一8() 所示。 2、三视图的投影规律 从图2一9可以看出,一个视图只能反映两个方向的尺寸,主视图反映了物体的长度和高度, 俯视图反映了物体的长度和宽度,左视图反映了物体的宽度和高度。由此可以归纳出三视图的投 影规律: 主、俯视图“长对正”(即等长): 主、左视图“高平齐”(即等高): 俯、左视图“宽相等”(即等宽): 三视图的投影规律反映了三视图的重要特性,也是画图和读图的依据。无论是整个物体还是
(c) (d) 图 2-8 三视图的形成遇展开 (3)三投影面体系的展开 在实际作图中,为了画图方便,需要将三个投影面在一个平面(纸面)上表示出来,规定: 使 V 面不动,H 面绕 OX 轴向下旋转 90°与 V 面重合,W 面绕 OZ 轴向右旋转 90°与 V 面重合, 这样就得到了在同一平面上的三视图,如图 2-8(b)所示。可以看出,俯视图在主视图的下方, 左视图在主视图的右方。在这里应特别注意的是:同一条 OY 轴旋转后出现了两个位置,因为 OY 是 H 面和 W 面的交线,也就是两投影面的共有线,所以 OY 轴随着 H 面旋转到 OYH 的位置,同 时又随着 W 面旋转到 OYW 的位置。为了作图简便,投影图中不必画出投影面的边框,如图 2-8 (c)所示。由于画三视图时主要依据投影规律,所以投影轴也可以进一步省略,如图 2-8(d) 所示。 2、三视图的投影规律 从图 2-9 可以看出,一个视图只能反映两个方向的尺寸,主视图反映了物体的长度和高度, 俯视图反映了物体的长度和宽度,左视图反映了物体的宽度和高度。由此可以归纳出三视图的投 影规律: 主、俯视图“长对正”(即等长); 主、左视图“高平齐”(即等高); 俯、左视图“宽相等”(即等宽); 三视图的投影规律反映了三视图的重要特性,也是画图和读图的依据。无论是整个物体还是