
第十四讲§3一1基本几何体的投影及尺寸标注 课题:1、平面立体的投影及表面取点 2、曲面立体的投影及表面取点 课堂类型:讲授 教学目的:1、讲解平面立体和曲面立体的种类及其三视图画法 2、讲解在平面立体和圆柱体表面取点、取线的作图方法 教学要求:1、能够熟练掌握平面立体和圆柱体的三视图画法 2、能够熟练运用利用点所在的面的积聚性法和辅助线法在平面立体和圆柱体表 面取点、取线 教学重点:1、平面立体和曲面立体的种类及其三视图画法。 2、在平面立体和圆柱体表面取点、取线的作图方法 教学难点:在圆柱体表面取点、取线的作图方法 敕具:基本体模型:三棱柱、四棱柱、五棱柱、六棱柱、三棱锥、四棱锥、圆柱体等 教学方法:用教学模型辅助讲解。 教学过程: 一、复习旧课 结合作业复习直线和平面投影变换的作图方法和步骤。 二、引入新课题 机器上的零件,不论形状多么复杂,都可以看作是由基本几何体按照不同的方式组合而 成的。 基本几何体一表面规则而单一的几何体。按其表面性质,可以分为平面立体和曲面立 体两类。 1、平面立体一一立体表面全部由平面所围成的立体,如棱柱和棱锥等。(出示模型给学生看)。 2、曲面立体一一立体表面全部由曲面或曲面和平面所围成的立体,如圆柱、圆锥、圆球等。 (出示模型给学生看)。曲面立体也称为回转体。 三、教学内容 (一)平面立体的投影及表面取点 1、棱柱 棱柱由两个底面和棱面组成,棱面与棱面的交线称为棱线,棱线互相平行。棱线与底面
第十四讲 §3—1 基本几何体的投影及尺寸标注 课 题:1、平面立体的投影及表面取点 2、曲面立体的投影及表面取点 课堂类型:讲授 教学目的:1、讲解平面立体和曲面立体的种类及其三视图画法 2、讲解在平面立体和圆柱体表面取点、取线的作图方法 教学要求:1、能够熟练掌握平面立体和圆柱体的三视图画法 2、能够熟练运用利用点所在的面的积聚性法和辅助线法在平面立体和圆柱体表 面取点、取线 教学重点:1、平面立体和曲面立体的种类及其三视图画法。 2、在平面立体和圆柱体表面取点、取线的作图方法 教学难点:在圆柱体表面取点、取线的作图方法 教 具:基本体模型:三棱柱、四棱柱、五棱柱、六棱柱、三棱锥、四棱锥、圆柱体等 教学方法:用教学模型辅助讲解。 教学过程: 一、复习旧课 结合作业复习直线和平面投影变换的作图方法和步骤。 二、引入新课题 机器上的零件,不论形状多么复杂,都可以看作是由基本几何体按照不同的方式组合而 成的。 基本几何体——表面规则而单一的几何体。按其表面性质,可以分为平面立体和曲面立 体两类。 1、平面立体——立体表面全部由平面所围成的立体,如棱柱和棱锥等。(出示模型给学生看)。 2、曲面立体——立体表面全部由曲面或曲面和平面所围成的立体,如圆柱、圆锥、圆球等。 (出示模型给学生看)。曲面立体也称为回转体。 三、教学内容 (一)平面立体的投影及表面取点 1、棱柱 棱柱由两个底面和棱面组成,棱面与棱面的交线称为棱线,棱线互相平行。棱线与底面
垂直的棱柱称为正棱柱。本节仅讨论正棱柱的投影。 (1)棱柱的投影 以正六棱柱为例。如图3一1(a)所示为一正六棱柱,由上、下两个底面(正六边形) 和六个棱面(长方形)组成。设将其放置成上、下底面与水平投影面平行,并有两个棱面平 行于正投影面面。 上、下两底面均为水平面,它们的水平投影重合并反映实形,正面及侧面投影积聚为两 条相互平行的直线。六个棱面中的前、后两个为正平面,它们的正面投影反映实形,水平投 影及侧面投影积聚为一直线。其他四个棱面均为铅垂面,其水平投影均积聚为直线,正面投 影和侧面投影均为类似形。 a( b(c) 0c (a)立体图 (b)投影图 图3一1正大棱柱的投影及表面上的点 边画图边讲解作图方法与步骤。 总结正棱柱的投影特征:当棱柱的底面平行某一个投影面时,则棱柱在该投影面上投影 的外轮廊为与其底面全等的正多边形,而另外两个投影则由若干个相邻的炬形线框所组成。 (2)棱柱表面上点的投影 方法:利用点所在的面的积聚性法。(因为正棱柱的各个面均为特殊位置面,均具有积 聚性。) 平面立体表面上取点实际就是在平面上取点。首先应确定点位于立体的哪个平面上,并 分析该平面的投影特性,然后再根据点的投影规律求得。 举例:如图3一1(b)所示,己知棱柱表面上点M的正面投影m',求作它的其他两
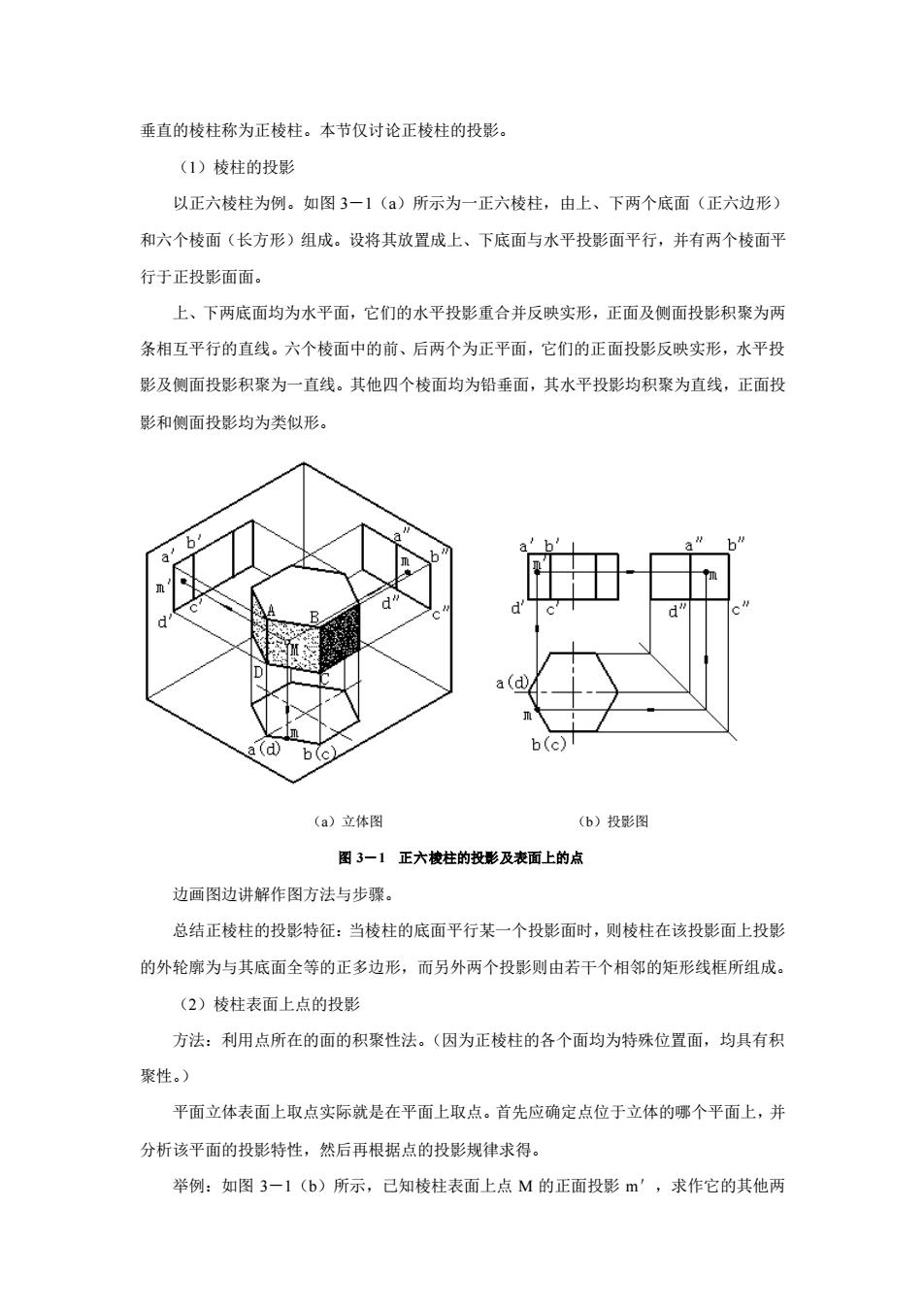
垂直的棱柱称为正棱柱。本节仅讨论正棱柱的投影。 (1)棱柱的投影 以正六棱柱为例。如图 3-1(a)所示为一正六棱柱,由上、下两个底面(正六边形) 和六个棱面(长方形)组成。设将其放置成上、下底面与水平投影面平行,并有两个棱面平 行于正投影面面。 上、下两底面均为水平面,它们的水平投影重合并反映实形,正面及侧面投影积聚为两 条相互平行的直线。六个棱面中的前、后两个为正平面,它们的正面投影反映实形,水平投 影及侧面投影积聚为一直线。其他四个棱面均为铅垂面,其水平投影均积聚为直线,正面投 影和侧面投影均为类似形。 (a)立体图 (b)投影图 图 3-1 正六棱柱的投影及表面上的点 边画图边讲解作图方法与步骤。 总结正棱柱的投影特征:当棱柱的底面平行某一个投影面时,则棱柱在该投影面上投影 的外轮廓为与其底面全等的正多边形,而另外两个投影则由若干个相邻的矩形线框所组成。 (2)棱柱表面上点的投影 方法:利用点所在的面的积聚性法。(因为正棱柱的各个面均为特殊位置面,均具有积 聚性。) 平面立体表面上取点实际就是在平面上取点。首先应确定点位于立体的哪个平面上,并 分析该平面的投影特性,然后再根据点的投影规律求得。 举例:如图 3-1(b)所示,已知棱柱表面上点 M 的正面投影 m′,求作它的其他两

面投影m、m”。因为m'可见,所以点M必在面ABCD上。此棱面是铅垂面,其水平投 影积聚成一条直线,故点M的水平投影m必在此直线上,再根据m、m'可求出m”。由 于ABCD的侧面投影为可见,故m”也为可见。 特别强调:点与积聚成直线的平面重影时,不加括号。 2、棱锥 (1)棱维的投影 以正三棱锥为例。如图3一2()所示为一正三棱锥,它的表面由一个底面(正三边形) 和三个侧棱面(等腰三角形)围成,设将其放置成底面与水平投影面平行,并有一个棱面垂 直于侧投影面。 由于维底面△ABC为水平面,所以它的水平投影反映实形,正面投影和侧面投影分别 积聚为直线段abc和a"(e”)b"。棱面△SAC为侧垂面,它的侧面投影积聚为一段斜线 s"a"(c),正面投影和水平投影为类似形△sac和△sc,前者为不可见,后者可见。棱面 △SAB和△SBC均为一般位置平面,它们的三面投影均为类似形。 棱线SB为侧平线,棱线SA、SC为一般位置直线,棱线AC为侧垂线,棱线AB、BC 为水平线。 (a)立体图 (b)投影图 图3一2正三梭锥的投影及表面上的点 边画图边讲解作图方法与步骤。 总结正棱锥的投影特征:当棱锥的底面平行某一个投影面时,则棱锥在该投影面上投影 的外轮廓为与其底面全等的正多边形,而另外两个投影则由若干个相邻的三角形线框所组
面投影 m、m″。因为 m′可见,所以点 M 必在面 ABCD 上。此棱面是铅垂面,其水平投 影积聚成一条直线,故点 M 的水平投影 m 必在此直线上,再根据 m、m′ 可求出 m″。由 于 ABCD 的侧面投影为可见,故 m″ 也为可见。 特别强调:点与积聚成直线的平面重影时,不加括号。 2、棱锥 (1)棱锥的投影 以正三棱锥为例。如图 3-2(a)所示为一正三棱锥,它的表面由一个底面(正三边形) 和三个侧棱面(等腰三角形)围成,设将其放置成底面与水平投影面平行,并有一个棱面垂 直于侧投影面。 由于锥底面△ABC 为水平面,所以它的水平投影反映实形,正面投影和侧面投影分别 积聚为直线段 a′b′c′ 和 a″(c″ )b″。棱面△SAC 为侧垂面,它的侧面投影积聚为一段斜线 s″a″(c″),正面投影和水平投影为类似形△s′a′c′ 和△sac,前者为不可见,后者可见。棱面 △SAB 和△SBC 均为一般位置平面,它们的三面投影均为类似形。 棱线 SB 为侧平线,棱线 SA、SC 为一般位置直线,棱线 AC 为侧垂线,棱线 AB、BC 为水平线。 (a)立体图 (b)投影图 图 3-2 正三棱锥的投影及表面上的点 边画图边讲解作图方法与步骤。 总结正棱锥的投影特征:当棱锥的底面平行某一个投影面时,则棱锥在该投影面上投影 的外轮廓为与其底面全等的正多边形,而另外两个投影则由若干个相邻的三角形线框所组

成。 (2)棱维表面上点的投影 方法:1)利用点所在的面的积聚性法。 2)辅助线法。 首先确定点位于棱锥的哪个平面上,再分析该平面的投影特性。若该平面为特殊位置平 面,可利用投影的积聚性直接求得点的投影:若该平面为一般位置平面,可通过辅助线法求 得。 举例:如图3一2(b)所示,已知正三棱锥表面上点M的正面投影m和点N的水平 面投影n,求作M、N两点的其余投影。 因为m'可见,因此点M必定在△SAB上。△SAB是一般位置平面,采用辅助线法, 过点M及锥项点S作一条直线SK,与底边AB交于点K。图3一2中即过m'作sk,再作 出其水平投影sk。由于点M属于直线SK,根据点在直线上的从属性质可知m必在sk上, 求出水平投影m,再根据m、m'可求出m”。 因为点N不可见,故点N必定在棱面△SAC上。棱面△SAC为侧垂面,它的侧面投影 积聚为直线段s”a”(c"),因此n"必在s”a”(c")上,由n、n”即可求出n。 (二)曲面立体的投影及表面取点 曲面立体的曲面是由一条母线(直线或曲线)绕定轴回转而形成的。在投影图上表示曲 面立体就是把围成立体的回转面或平面与回转面表示出来。 1、圆柱 圆柱表面由圆柱面和两底面所围成。圆柱面可看作一条直母线AB围绕与它平行的轴线 O0回转而成。圆柱面上任意一条平行于轴线的直线,称为圆柱面的素线。 (1)圆柱的投影 画图时,一般常使它的轴线垂直于某个投影面。 举例:如图3一4()所示,圆柱的轴线垂直于侧面,圆柱面上所有素线都是侧垂线, 因此圆柱面的侧面投影积聚成为一个圆。圆柱左、右两个底面的侧面投影反映实形并与该圆 重合。两条相互垂直的点划线,表示确定圆心的对称中心线。圆柱面的正面投影是一个矩形, 是圆柱面前半部与后半部的重合投影,其左右两边分别为左右两底面的积聚性投影,上、下 两边aa1、bb1分别是圆柱最上、最下素线的投影。最上、最下两条素线AA、BB1是圆柱 面由前向后的转向线,是正面投影中可见的前半圆柱面和不可见的后半圆柱面的分界线,也 称为正面投影的转向轮廓素线。同理,可对水平投影中的矩形进行类似的分析
成。 (2)棱锥表面上点的投影 方法:1)利用点所在的面的积聚性法。 2)辅助线法。 首先确定点位于棱锥的哪个平面上,再分析该平面的投影特性。若该平面为特殊位置平 面,可利用投影的积聚性直接求得点的投影;若该平面为一般位置平面,可通过辅助线法求 得。 举例:如图 3-2(b)所示,已知正三棱锥表面上点 M 的正面投影 m′ 和点 N 的水平 面投影 n,求作 M、N 两点的其余投影。 因为 m′ 可见,因此点 M 必定在△SAB 上。△SAB 是一般位置平面,采用辅助线法, 过点 M 及锥顶点 S 作一条直线 SK,与底边 AB 交于点 K。图 3-2 中即过 m′ 作 s′ k′,再作 出其水平投影 sk。由于点 M 属于直线 SK,根据点在直线上的从属性质可知 m 必在 s k 上, 求出水平投影 m,再根据 m、m′ 可求出 m″。 因为点 N 不可见,故点 N 必定在棱面△SAC 上。棱面△SAC 为侧垂面,它的侧面投影 积聚为直线段 s″a″(c″),因此 n″ 必在 s″a″(c″)上,由 n、n″ 即可求出 n′。 (二)曲面立体的投影及表面取点 曲面立体的曲面是由一条母线(直线或曲线)绕定轴回转而形成的。在投影图上表示曲 面立体就是把围成立体的回转面或平面与回转面表示出来。 1、圆柱 圆柱表面由圆柱面和两底面所围成。圆柱面可看作一条直母线 AB 围绕与它平行的轴线 OO1 回转而成。圆柱面上任意一条平行于轴线的直线,称为圆柱面的素线。 (1)圆柱的投影 画图时,一般常使它的轴线垂直于某个投影面。 举例:如图 3-4(a)所示,圆柱的轴线垂直于侧面,圆柱面上所有素线都是侧垂线, 因此圆柱面的侧面投影积聚成为一个圆。圆柱左、右两个底面的侧面投影反映实形并与该圆 重合。两条相互垂直的点划线,表示确定圆心的对称中心线。圆柱面的正面投影是一个矩形, 是圆柱面前半部与后半部的重合投影,其左右两边分别为左右两底面的积聚性投影,上、下 两边 a′a′1、b′b′1 分别是圆柱最上、最下素线的投影。最上、最下两条素线 AA1、BB1 是圆柱 面由前向后的转向线,是正面投影中可见的前半圆柱面和不可见的后半圆柱面的分界线,也 称为正面投影的转向轮廓素线。同理,可对水平投影中的矩形进行类似的分析

b】 (a)立体图 (b)投影图 图3一4柱的投影及表面上的点 边画图边讲解作图方法与步骤。 总结圆柱的投影特征:当圆柱的轴线垂直某一个投影面时,必有一个投影为圆形,另外 两个投影为全等的矩形。 (2)圆柱面上点的投影 方法:利用点所在的面的积聚性法。(因为圆柱的圆柱面和两底面均至少有一个投影具 有积聚性。) 举例:如图3一4(b)所示,己知圆柱面上点M的正面投影m,求作点M的其余两个 投影。 因为圆柱面的投影具有积聚性,圆柱面上点的侧面投影一定重影在圆周上。又因为m' 可见,所以点M必在前半圆柱面的上边,由m求得m”,再由m'和m”求得m。 四、小结 1、棱柱、棱维、圆柱体的投影分析和投影特征。 2、棱柱、棱锥、圆柱体上表面求点的方法。 五、布置作业 习题集3-1(1)(2)、(3)
(a)立体图 (b)投影图 图 3-4 圆柱的投影及表面上的点 边画图边讲解作图方法与步骤。 总结圆柱的投影特征:当圆柱的轴线垂直某一个投影面时,必有一个投影为圆形,另外 两个投影为全等的矩形。 (2)圆柱面上点的投影 方法:利用点所在的面的积聚性法。(因为圆柱的圆柱面和两底面均至少有一个投影具 有积聚性。) 举例:如图 3-4(b)所示,已知圆柱面上点 M 的正面投影 m′,求作点 M 的其余两个 投影。 因为圆柱面的投影具有积聚性,圆柱面上点的侧面投影一定重影在圆周上。又因为 m′ 可见,所以点 M 必在前半圆柱面的上边,由 m′ 求得 m″,再由 m′ 和 m″ 求得 m。 四、小结 1、棱柱、棱锥、圆柱体的投影分析和投影特征。 2、棱柱、棱锥、圆柱体上表面求点的方法。 五、布置作业 习题集 3-1(1)、(2)、(3)