
第七章X之枪验 第二节完全随机设计下两组频数分布的X2检验 。四格表专用公式: 7-a+0-d (ad-ben 完全随机设计下两组频数分布的四格表 属性 处理 合计 阳性 阴性 1组 a(T11) b(T12) a+b(固定值) 2组 c(T21) d(T22) c+d(固定值) 合计 a+c b+d n
第七章 χ 2 检 验 第二节 完全随机设计下两组频数分布的χ2检验 四格表专用公式: ( ) (a b)(c d )(a c)(b d ) a d bc n + + + + − = 2 2 处理 属性 合计 阳性 阴性 1 组 a(T11) b(T12) a+b(固定值) 2 组 c(T21) d(T22) c+d(固定值) 合计 a+c b+d n 完全随机设计下两组频数分布的四格表

第七章X之检验 第二节完全随机设计下两组频数分布的X2检验 。四格表专用公式:(<T≥5,且n≥40) x- (ad-beyn (a+bXc+a)a+c)b+d) (41×11-24×42×80 =6.565 45×35×65×15
第七章 χ 2 检 验 第二节 完全随机设计下两组频数分布的χ2检验 四格表专用公式:(<T5,且n 40) ( ) ( )( )( )( ) ( ) 6.565 4 5 3 5 6 5 1 5 4 1 1 1 2 4 4 8 0 2 2 2 = − = + + + + − = a b c d a c b d a d bc n

第七章X枪验 第二节完全随机设计下两组频数分布的X2检验 。四格表校正公式:当(1≤T<5,且n 40)需校正 (d-如-gn x'-(a+bXc+dYa+cX+d) :=z47刀小-05 T
第七章 χ 2 检 验 第二节 完全随机设计下两组频数分布的χ2检验 四格表校正公式 :当(1T<5,且n 40)需校正 (a b)(c d )(a c)(b d ) n n a d bc + + + + − − = 2 2 2 ( ) − − = T A T 2 2 0.5
第七章X之检验 第二节完全随机设计下两组频数分布的X2检验 例7-3将病情相似的淋巴系肿瘤患者随机分成两组, 分别做单纯化疗与复合化疗,两组的缓解率见下表, 试问两疗法的总体缓解率是否不同? 两种疗法缓解率的比较 属性 组别 合计 缓解率(o) 缓解 未缓解 单纯化疗 2(4.8) 10(7.2) 12(固定值) 16.7 复合化疗 14(11.2) 14(16.8) 28(固定值) 50.0 合计 16 24 40 40.0
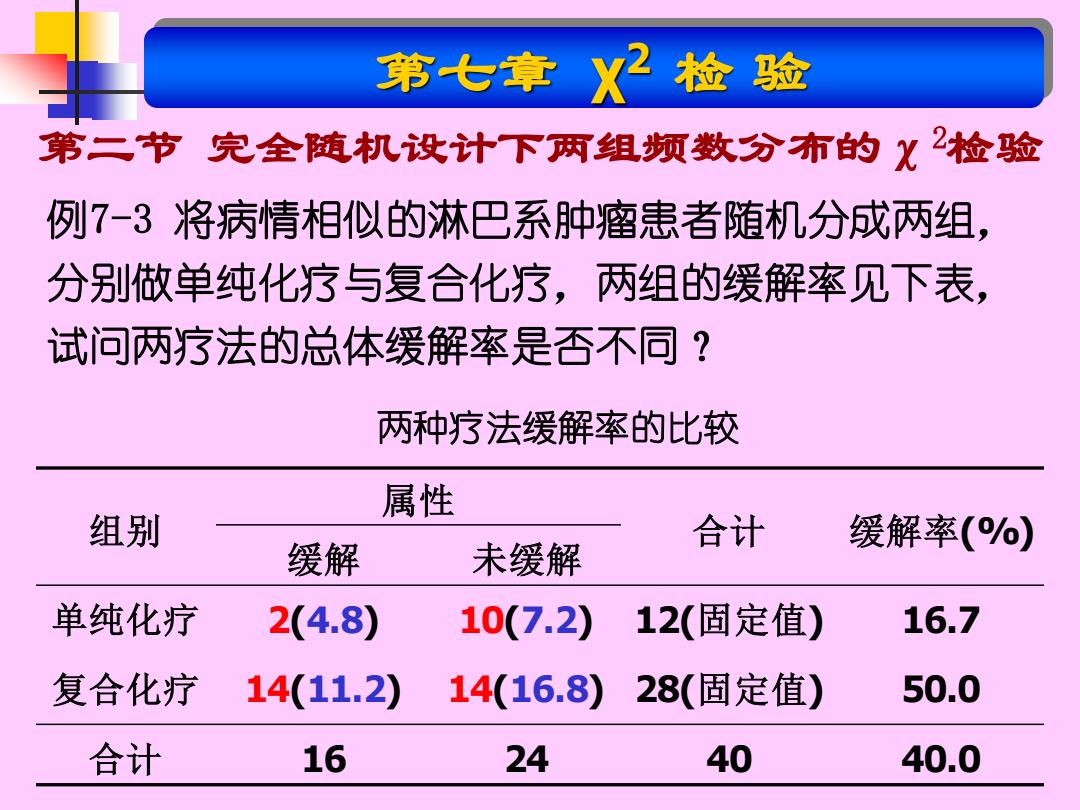
第七章 χ 2 检 验 第二节 完全随机设计下两组频数分布的χ2检验 例7-3 将病情相似的淋巴系肿瘤患者随机分成两组, 分别做单纯化疗与复合化疗,两组的缓解率见下表, 试问两疗法的总体缓解率是否不同? 组别 属性 合计 缓解率(%) 缓解 未缓解 单纯化疗 2(4.8) 10(7.2) 12(固定值) 16.7 复合化疗 14(11.2) 14(16.8) 28(固定值) 50.0 合计 16 24 40 40.0 两种疗法缓解率的比较

第七章X枪验 第二节完全随机设计下两组频数分布的X2检验 1.建立检验假设并确定检验水准 H,:两法总体缓解概率相同,元元2 H1:两法总体缓解概率不同,元1≠元2a=0.05 2.计算检验统计量:H成立时,两组缓解概率相同, 均近似地等于合并估计的缓解概率,由此得到四格 表中每一格的理论数,1<T11〈5,n=40, 需采用校正公式
第七章 χ 2 检 验 第二节 完全随机设计下两组频数分布的χ2检验 1. 建立检验假设并确定检验水准 H0:两法总体缓解概率相同,π1=π2 H1:两法总体缓解概率不同,π1≠π2 α=0.05 2. 计算检验统计量:H0成立时,两组缓解概率相同, 均近似地等于合并估计的缓解概率,由此得到四格 表中每一格的理论数,1<T11<5,n=40, 需采用校正公式