
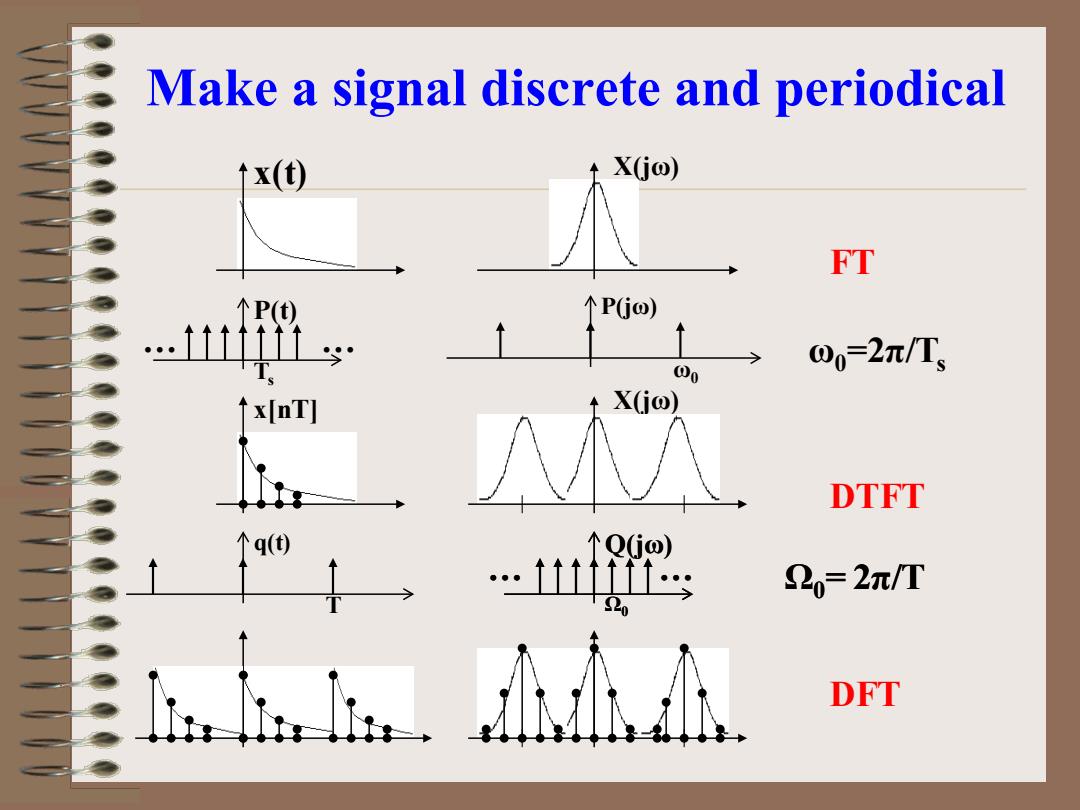
Make a signal discrete and periodical The engineering signals are often continue and aperiodical.If we want to process the signals with DFT,we have to make the signals discrete and periodical. Sampling to make the signal discrete .Make the signal periodical: -If x[n]is a limited length N-point sequence,see it as one period of a periodical signal that means extend it to a periodical "If x[n]is an infinite length sequence,cut-off its tail to make a N-point sequence,then do the periodic extending.The tail cutting-off will introduce distortion.We must develop truncation algorithm to reduce the error,which is windowing
Make a signal discrete and periodical • The engineering signals are often continue and aperiodical. If we want to process the signals with DFT, we have to make the signals discrete and periodical. •Sampling to make the signal discrete •Make the signal periodical: If x[n] is a limited length N-point sequence, see it as one period of a periodical signal that means extend it to a periodical If x[n] is an infinite length sequence, cut-off its tail to make a N-point sequence, then do the periodic extending. The tail cutting-off will introduce distortion. We must develop truncation algorithm to reduce the error, which is windowing
Make a signal discrete and periodical x() X(jo) FT 个P() 个PGo) 00=2π/T 00 xnT] X(jo) DTFT a(f 20=2m/T DFT
Make a signal discrete and periodical x(t) X(jω) P(jω) ω0 ω0=2π/Ts x[nT] X(jω) q(t) T FT DFT DTFT Q(jω) Ω0 … … Ω0 = 2π/T Q(jω) Ω0 … … Ω0 = 2π/T P(t) Ts … …

S 3.3 Discrete Fourier Transform (DFT) Definition-The simplest relation between a length-N sequence x[n], defined for Osn <N-1,and its DTFT X(ei) is obtained by uniformly sampling X(ei) on the o-axis between 0<o≤2πat ok=2πk/N,0sk≤N-1 From the definition of the DTFT have W-1 XIk]=X(e/0) =∑x[nl]eJ2πk/N 0=2元k/N n=0 0≤k≤W-1
§3.3 Discrete Fourier Transform (DFT) • Definition - The simplest relation between a length-N sequence x[n], defined for 0≤n ≤N-1, and its DTFT X(ejω) is obtained by uniformly sampling X(ejω) on the ω-axis between 0≤ω ≤2π at ωk=2πk/N , 0≤k≤N-1 • From the definition of the DTFT have [ ] ( ) [ ] , 1 0 2 / 2 / = = ∑ − = − π ω= π ω N n j k N k N j X k X e x n e 0 ≤ k ≤ N −1

S 3.3 Discrete Fourier Transform DFT) Note:X[k]is also a length-N sequence in the frequency domain The sequence X[k]is called the Discrete Fourier Transform (DFT)of the sequence xn Using the notation W=e-j2 /N the DFT is usually expressed as: N- X[k]=∑x[nW,0≤k≤N-1 n=0
§3.3 Discrete Fourier Transform (DFT) • Note: X[k] is also a length-N sequence in the frequency domain • The sequence X[k] is called the Discrete Fourier Transform (DFT) of the sequence x[n] • Using the notation WN=e-j2 π/N the DFT is usually expressed as: [ ] [ ] , 0 1 1 0 = ∑ ≤ ≤ − − = X k x n W k N N n kn N

3.3 Discrete Fourier Transform (DFT) The Inverse Discrete Fourier Transform (IDFT)is given by 1W-1 x[n]= ∑X[k]Ww,0≤n ≤W-1 N k=0
§3.3 Discrete Fourier Transform (DFT) • The Inverse Discrete Fourier Transform (IDFT) is given by [ ] , 0 1 1 [ ] 1 0 = ∑ ≤ ≤ − − = − X k W n N N x n N k kn N