
将此种关系用于理想气体 c-c-〔+P品 140 对于理想气体 ,-0 C,-G=号”=R Cpm-Cvm=R (15) 绝热过程的功和绝热过程方程 在绝热过程中,系统和环境之间没有热量交换,根据热力学第一定律,体系做的功必然以 内能的降低为代价 80=0dU=-6W 如果功仅为体积功 δW=Pd 即 dU+pdΨ=0 对理想气体而言 dU=CydTCydT+pdy=0 如果G为常数 W=C(T-T) 理想气体的绝热可逆过程方程 由 -dU pdv 在可逆过程中 P.=p=nRTIV 4r0 由 C。-C=nR cdr+G=G上ar-0 dr_C。-Cdr C.V 令:Y=C,1C,且其比值假想为常数 -9-6-咒 nT=-(-1)n'+常数 .TV=常数 (16) nR代入上式 pT=常数 (17) P代入上式prT" (18) 以上三个方程是理想气体在绝热可逆过程中所遵循的方程式 理想气体的绝热过程方程和状态方程的比较 理想气体在绝热过程中做的功 1.根据能量关系求功 W=C(T-T) 2.由功的定义式 w-
将此种关系用于理想气体 T P P V T V P V U C C + − = (14) 对于理想气体 = 0 V T U nR P nRT T CP CV P P = − = ( ) 或 CP,m −CV ,m = R (15) 绝热过程的功和绝热过程方程 在绝热过程中,系统和环境之间没有热量交换,根据热力学第一定律,体系做的功必然以 内能的降低为代价 Q = 0 dU = − W 如果功仅为体积功 W = PdV 即 dU + pdV = 0 对理想气体而言 dU = CV dT CV dT + pdv = 0, 如果 CV为常数 ( ) W = CV T1 −T2 理想气体的绝热可逆过程方程 由 − dU = pedV 在可逆过程中 pe = p = nRT /V + dV = 0 V nRT CV dT 由 Cp − CV = nR ( ) = 0 − + dV V C C T C dT p V V V dV C C C T dT v p − V − = 令: Cp CV = / , 且其比值假想为常数 ( ) − = − V dV T dT 1 nT = −( − 1)nV + 常数 = −1 TV 常数 (16) 将 nR pV T = 代入上式 = pV 常数 (17) 将 P nRT V = 代入上式 p T 1− (18) 以上三个方程是理想气体在绝热可逆过程中所遵循的方程式 理想气体的绝热过程方程和状态方程的比较 理想气体在绝热过程中做的功 1. 根据能量关系求功 ( ) W = CV T1 −T2 2. 由功的定义式 ( ) 2 1 2 1 2 1 ] 1 1 [ 1 V V V V V V V K dV V K W pdV − − = = = −
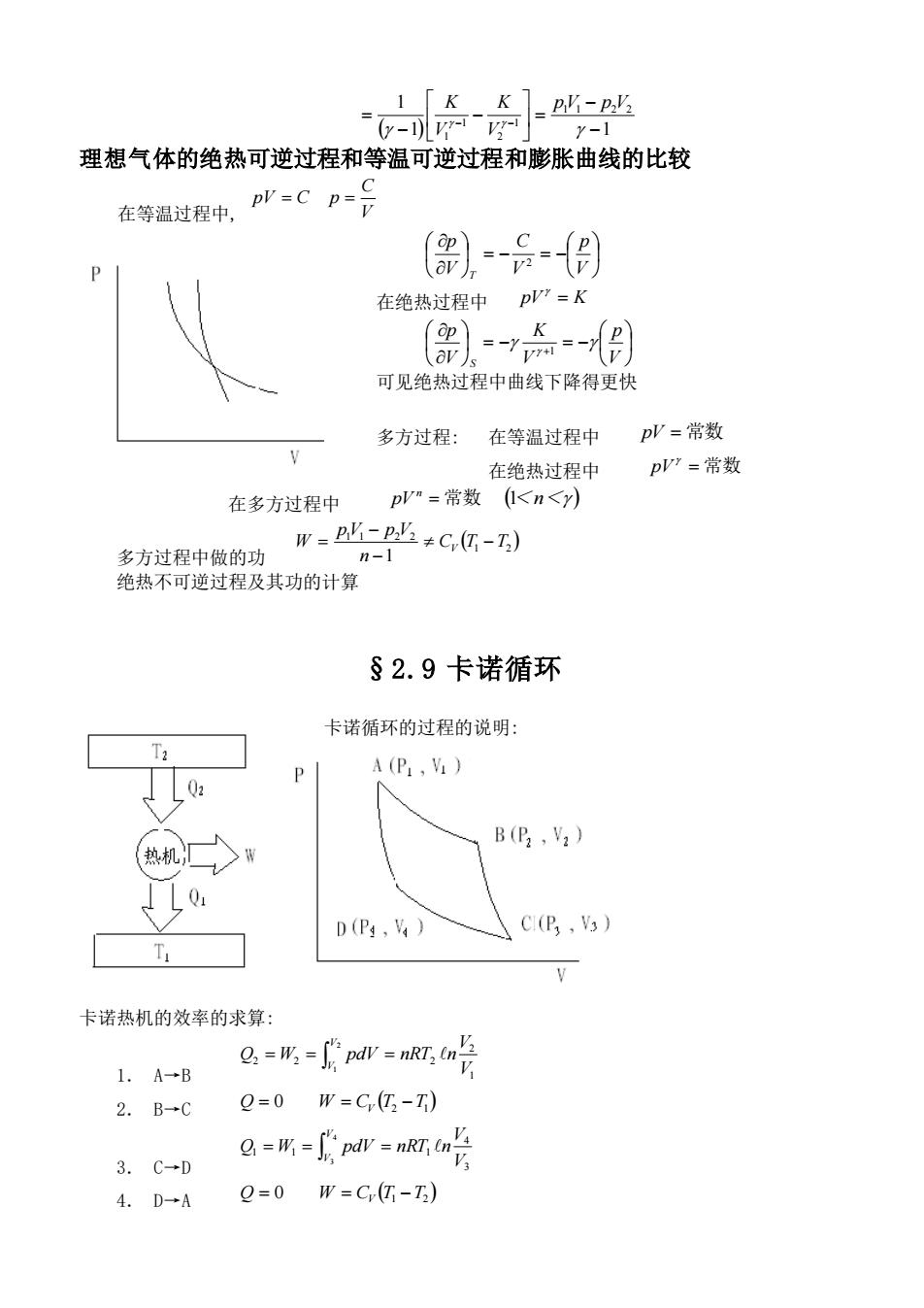
理想气体的绝热可逆过程和等温可逆过程和膨胀曲线的比较 在等温过程中,p:Cp-号 在绝热过程中p”=K 可见绝热过程中曲线下降得更快 多方过程: 在等温过程中 pP=常数 在绝热过程中 pP'=常数 在多方过程中 pV"=常数<n<y) 多方过程中做的功 w=业-业+C-) n-1 绝热不可逆过程及其功的计算 §2.9卡诺循环 卡诺循环的过程的说明 Ta A (P V B(E2,V2) 热机 .Q: D (P ,V) C(B,) 卡诺热机的效率的求算: g,=所=na=nRr,n 1.A→B 2.B→C Q=0W=C(亿-T) 3.C-D g=所-斯pr=na2 4.D-→AQ=0W=C(G-T)
( 1) 1 1 1 1 2 2 1 2 1 1 − − = − − = − − pV p V V K V K 理想气体的绝热可逆过程和等温可逆过程和膨胀曲线的比较 在等温过程中, V C pV = C p = = − = − V p V C V p T 2 在绝热过程中 pV = K = − = − + V p V K V p S 1 可见绝热过程中曲线下降得更快 多方过程: 在等温过程中 pV = 常数 在绝热过程中 pV = 常数 在多方过程中 pV n = 常数 (1<n< ) 多方过程中做的功 ( ) 1 2 1 1 2 2 1 C T T n pV p V W V − − − = 绝热不可逆过程及其功的计算 §2.9 卡诺循环 卡诺循环的过程的说明: 卡诺热机的效率的求算: 1. A→B = = = 2 1 1 2 2 2 2 V V V V Q W pdV nRT n 2. B→C ( ) Q = 0 W = CV T2 −T1 3. C→D = = = 4 3 3 4 1 1 1 V V V V Q W pdV nRT n 4. D→A ( ) Q = 0 W = CV T1 −T2

卡诺热机在循环过程中所做的功 W=用+用+W+用 由理想气体的绝热过程方程 TV-=TV- W=TVI 两式相除 g可 2.W=nRT,tn-nRT,cn=nR(-T)tn g,=形-pa=n,a9 热机从高温热源吸收之热 热机的效率 n-1-2 可见,热机的效率只和热源的温度有关,而和工作的物质无关 7=3坦=1+g 同样,热机的效率也可以写成 02 02 则有 Γ五g g+9=0 (19) 即卡诺循环的热温商之和为零
卡诺热机在循环过程中所做的功 W = W1 +W2 +W3 +W3 3 4 1 1 2 2 V V nRT n V V = nRT n + 由理想气体的绝热过程方程 1 1 3 1 2 2 − − = T V TV 1 1 4 1 2 1 − − = T V TV 两式相除 4 3 1 2 V V V V = 1 2 2 1 1 2 1 1 2 2 ( ) V V nR T T n V V nRT n V V W = nRT n − = − 热机从高温热源吸收之热 = = = 2 1 1 2 2 2 2 V V V V Q W pdV nRT n 热机的效率 2 1 2 2 1 1 T T T T T = − − = 可见,热机的效率只和热源的温度有关,而和工作的物质无关 同样,热机的效率也可以写成 2 1 2 2 1 1 Q Q Q Q Q = + + = 则有 2 1 2 1 Q Q T T − = 或 0 2 2 1 1 + = T Q T Q (19) 即卡诺循环的热温商之和为零

山东理工大学教案 第5☐ 次课教学课型:理论课实验课口习课口实践课口技能课口其它口 主要教学内容(注明:·重点#难点): §2.10 Joule-Thomson效应-实际气体的△U和△H 52.11热化学 S2.12Hes定律 #(1)」-T实验及结论 (2)μ灯系数的定义及应用意义: 气体液化的T、P选择 (3)实际气体的内能知格 (4)化学反应热效应的定义 (5)定压反应热Q,与定容反应热Q关系 #(6)反应进度:定义特征 (7)摩尔反应烙 (8)标准摩尔反应焓,热化学标准态的规定 幸(9)盖断定律 可以根据己经准确测定了的反应热,来计算难于测定或根本不能测定的反应热 可以根据已知的反应热,计算出未知的反应热 教学目的要求: 掌握理想气体的绝热可逆过程方程式 掌握理想气体的绝热过程功的求算 了解」-T实验及结论的意义 教学方法和教学手段: 讲授,多媒体 讨论、思考题、作业: 习题: 27 《物理化学解题指导》,孙德坤, 沈文霞等,江苏教有出版社,1998年 《物理化学》,刁兆玉,姜云生等,山东教育出版社,1994年 《物理化学题解》,李忠德,向建敏等,华中科技大学出版社,2002 注:教师讲稿附后
山 东 理 工 大 学 教 案 第 5 次课 教学课型:理论课□ 实验课□ 习题课□ 实践课□ 技能课□ 其它□ 主要教学内容(注明:* 重点 # 难点 ): §2.10 Joule-Thomson 效应-实际气体的ΔU 和ΔH §2.11 热化学 §2.12 Hess 定律 #(1)J-T 实验及结论 (2)μJ-T系数的定义及应用意义: 气体液化的 T、P 选择 (3)实际气体的内能和焓 (4)化学反应热效应的定义 (5)定压反应热 Qp 与定容反应热 QV 关系 #(6)反应进度:定义 特征 (7)摩尔反应焓 (8)标准摩尔反应焓,热化学标准态的规定 *(9)盖斯定律 可以根据已经准确测定了的反应热,来计算难于测定或根本不能测定的反应热; 可以根据已知的反应热,计算出未知的反应热。 教学目的要求: 掌握理想气体的绝热可逆过程方程式 掌握理想气体的绝热过程功的求算 了解 J-T 实验及结论的意义 教学方法和教学手段: 讲授,多媒体 讨论、思考题、作业: 习题: 27 参考资料: 《物理化学解题指导》,孙德坤,沈文霞等,江苏教育出版社,1998 年 《物理化学》,刁兆玉,姜云生等,山东教育出版社,1994 年 《物理化学题解》,李忠德,向建敏等,华中科技大学出版社,2002 注:教师讲稿附后 √

§2.10 Joule-Thomson效应-实际气体的△U和△H 焦尔一汤姆逊效应 焦一汤实验(节流膨胀过程)及结果:在焦汤实验中,有的气体的温度上升,有的 气体的温度下降。 由焦一汤实验得到的结论:实验气体的热力 学能不但是温度的函数,而且是体积或压力的函 B 数。 设:在B及T时一定量的气体的体积为V, 经过节流膨胀以后,体积为,温度为五,压力 焦尔-一汤姆逊实验 为P。在节流膨胀的过程中,环境对体系做功为 BK,体系对环境做功为B。 环境所做的净功 W=(P,'-p) 由于节流膨胀为绝热过程 0=0 由热力学第一定律 △U=U2-U=-P,'+p 则有 U2+p=U+pU 如 H=H, (节流膨胀为恒焓过程) 焦一汤系数及对气体节流过程的分析 定义 (20) 从此定义可知,如节流膨胀中,温度降低,则“为正值:温度上升,“为负值,一般气体 在常温时的焦汤系数为正值,温度很低时,“为负值,但H和H在常温时“为负值, 焦汤系数及气体的转化曲线的测定 对气体来说 H=f(T.p) 节流膨胀后 (器),+,中 dH=0 Cp C 对理想气体来说 -[1-。-0 对于实际气体,由于实际气体分子之间的吸引力,恒温下膨胀时仰<0),内能增大
§2.10 Joule-Thomson 效应-实际气体的ΔU 和ΔH 焦尔—汤姆逊效应 焦—汤实验(节流膨胀过程)及结果:在焦汤实验中,有的气体的温度上升,有的 气体的温度下降。 由焦—汤实验得到的结论:实验气体的热力 学能不但是温度的函数,而且是体积或压力的函 数。 设:在 P1及 T1时一定量的气体的体积为 V1, 经过节流膨胀以后,体积为 V2,温度为 T2,压力 为 P2。在节流膨胀的过程中,环境对体系做功为 P1V1,体系对环境做功为 P2V2。 环境所做的净功 ( ) W = − p2V − p1V1 由于节流膨胀为绝热过程 Q = 0 由热力学第一定律 U =U2 −U1 = −p2V + p1V1 则有 U2 + p2V2 = U1 + p1U1 即 H1 = H2 (节流膨胀为恒焓过程) 焦—汤系数及对气体节流过程的分析 定义 H p T = (20) 从此定义可知,如节流膨胀中,温度降低,则 为正值;温度上升, 为负值,一般气体 在常温时的焦汤系数为正值,温度很低时, 为负值,但 H2和 He在常温时 为负值, 焦汤系数及气体的转化曲线的测定 对气体来说 H = f (T, p) 节流膨胀后 dp p H dT T H dH p T + = dH = 0 ( ) p T T p T H C p PV p U T H p H p T + − = − = = ( ) p T p T C p pV C p U − = − 对理想气体来说 ( ) = 0 = 0 = p T p pV p U 对于实际气体,由于实际气体分子之间的吸引力,恒温下膨胀时 (dp<0) ,内能增大