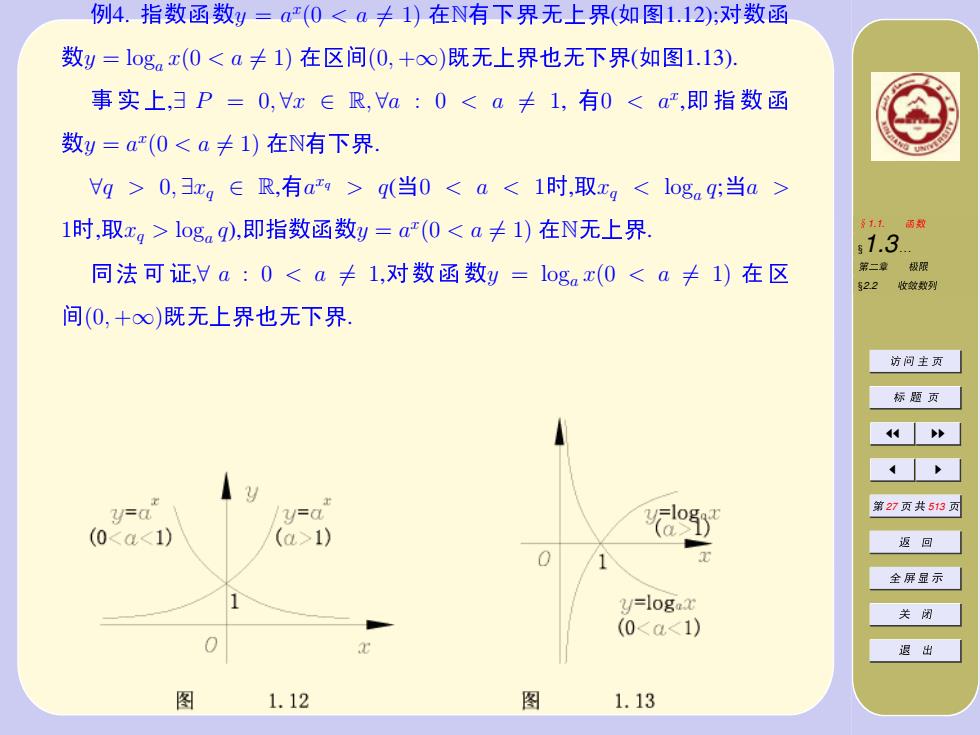
例4.指数函数y=a0<a卡1)在N有下界无上界(如图1.12):对数函 数y=log。x(0<a≠1)在区间(0,+∞)既无上界也无下界(如图1.13). 事实上,3P=0,x∈R,a:0<a≠1,有0<a,即指数函 数y=a(0<a卡1)在N有下界. g>0,3xg∈R,有a>q(当0<a<1时,取xg<loga q;当a> 1时,取xg>loga q),即指数函数y=a'(0<a≠1)在N无上界. 多11雨数 s1.3 同法可证,a:0<a卡1,对数函数y=loga(0<a卡1)在区 第二章极限 22 收效数列 间(0,+∞)既无上界也无下界 访问主页 标题页 炒 Va* y=a* 第27页共513页 (0<a<1) (a>1) 返回 0 全屏显示 2 y=logax 关闭 (0<a<1) 0 退出 图 1.12 图 1.13
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 27 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ⑦4. ➁ê➻êy = a x (0 < a 6= 1) ✸N❦❡✳➹þ✳(❳ã1.12);éê➻ êy = loga x(0 < a 6= 1) ✸➠♠(0, +∞)◗➹þ✳➃➹❡✳(❳ã1.13). ➥ ➣ þ,∃ P = 0, ∀x ∈ R, ∀a : 0 < a 6= 1, ❦0 < ax ,❂ ➁ ê ➻ êy = a x (0 < a 6= 1) ✸N❦❡✳. ∀q > 0, ∃xq ∈ R,❦a xq > q(✟0 < a < 1➒,✒xq < loga q;✟a > 1➒,✒xq > loga q),❂➁ê➻êy = a x (0 < a 6= 1) ✸N➹þ✳. Ó④➀②,∀ a : 0 < a 6= 1,éê➻êy = loga x(0 < a 6= 1) ✸➠ ♠(0, +∞)◗➹þ✳➃➹❡✳

1.1雨数 例5.数列{m}有下界无上界:数列{(-1)”n}既无上界也无下界.事实 s1.3 第二章极限 上,a≤1,都是数列{n}的下界;b>0,3no∈N+,有0>b,即数列{n}有下 $22收敛数列 界无上界 访问主页 3k∈N+,有(-1)2k2k=2k>b, 标题页 Vb>0, 3k∈N+,有(-1)2k+1(2k+1)=-(2k+1)<-b, 炒 即数列{(-1)”n}既无上界也无下界. 第28页共513页 返回 全屏显示 关闭 退出
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 28 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ⑦5. ê✎{n}❦❡✳➹þ✳;ê✎{(−1)nn}◗➹þ✳➃➹❡✳. ➥➣ þ,∀a 6 1,Ñ➫ê✎{n}✛❡✳;∀b > 0, ∃n0 ∈ N+,❦n0 > b,❂ê✎{n}❦❡ ✳➹þ✳. ∀ b > 0, ( ∃k ∈ N+, ❦(−1)2k2k = 2k > b, ∃k ∈ N+, ❦(−1)2k+1(2k + 1) = −(2k + 1) < −b, ❂ê✎{(−1)nn}◗➹þ✳➃➹❡✳

二、单调函数 定义设函数f(x)在数集A有定义若Va1,x2∈A,且x1<x2,有 多1.1雨数 f(x)<f(2)(f(x)>f(2), s1.3 第二章极服 $22收敛数列 称函数f(x)在A严格增加(严格减少).上图不等式改为 访问主页 f(x1)≤f(x2)(f(x1)≥f(x2) 标题页 称函数f(z)在A单调增加(单调减少). 函数f(x)在A严格增加、严格减少与单调增加、单调减少,统称为函 第29页共513页列 数f(x)在A单调.严格增加与严格减少统称为严格单调若A是区间,此区间 返回 成为函数f(c)的单调区间. 全屏显示 关闭 退出
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 29 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ✓✦ü◆➻ê ➼➶ ✗➻ê f(x) ✸ê✽A❦➼➶.❡∀x1, x2 ∈ A,❹x1 < x2,❦ f(x1) < f(x2) (f(x1) > f(x2)), →➻ê f(x) ✸Aî❶❖❭(î❶⑦✟).þãØ✤➟❯➃ f(x1) 6 f(x2) (f(x1) > f(x2)), →➻ê f(x) ✸Aü◆❖❭(ü◆⑦✟). ➻ê f(x) ✸Aî❶❖❭✦î❶⑦✟❺ü◆❖❭✦ü◆⑦✟,Ú→➃➻ ê f(x) ✸Aü◆.î❶❖❭❺î❶⑦✟Ú→➃î❶ü◆.❡A➫➠♠,❞➠♠ ↕➃➻ê f(x) ✛ü◆➠♠

例6.1)指数函数y=a当a>1时,在R严格增加;当0<a<1时,在R严 格减少(如图1.12). 2)对数函数y=loga,a>1时,在区间(0,+o)严格增加;当0<a< 1时,在区间(0,+o)严格减少(如图1.13) 1.1雨数 s1.3. 第二章极限 $22 收敏数列 2 访问主页 标题页 炒 2 warcsinr 第30页共513页 返回 全屏显示 关闭 退出 1.15
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 30 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ⑦6. 1)➁ê➻êy = a x ✟a > 1➒,✸Rî❶❖❭;✟0 < a < 1➒,✸Rî ❶⑦✟(❳ã1.12). 2)éê➻êy = loga x,a > 1➒, ✸➠♠(0, +∞)î❶❖❭;✟0 < a < 1➒,✸➠♠(0, +∞)î❶⑦✟(❳ã1.13)

3)反正切函数y=arctan z在R严格增加(如图1.l0) 4)反余切函数y=arccot在R严格减少(如图l.11). 多1.1雨数 3)反正弦函数y=arcsinx在区间[-1,1]严格增加(如图1.14), s1.3 第二设极服 3)反余弦函数y=arccosx在区间[-1,1]严格减少(如图1.15) $22收敛数列 例7.函数y=与y=sgnx在R都是单调增加(如图1.3与图1.5). 事实上,a1,x2∈R,且1<x2,有 访问主页 标题页 [c]≤[z2l与sgnx1≤sgnx2 W炒 例8. 数列{},{-}都是严格增加数 第31页共513页 列{}{}{-n都是严格减少. 返回 全屏显示 关闭 退出
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 31 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ 3)❻✔❷➻êy = arctan x✸Rî❶❖❭(❳ã1.10). 4)❻④❷➻êy = arccot x✸Rî❶⑦✟(❳ã1.11). 3)❻✔✉➻êy = arcsin x✸➠♠[-1,1]î❶❖❭(❳ã1.14). 3)❻④✉➻êy = arccos x✸➠♠[-1,1]î❶⑦✟(❳ã1.15). ⑦7. ➻êy = [x]❺y = sgnx✸RÑ➫ü◆❖❭(❳ã1.3❺ã1.5). ➥➣þ,∀x1, x2 ∈ R,❹x1 < x2,❦ [x1] 6 [x2] ❺ sgnx1 6 sgnx2 ⑦8. ê ✎ n n − 1 n o , {n!}, n − 1 n 2 o Ñ ➫ î ❶ ❖ ❭;ê ✎ n 1 n o , n n + 1 n o , {−n}Ñ➫î❶⑦✟