
第三章微分中值定理与导数应用 一、学时分配: 讲课学时:14习题课学时:2共16学时 二、基本内容 1.微分中值定理: 2.罗必达法则: 3.泰物公式: 4.函数单调性与曲线的凹凸性: 5.函数的极值与最大值最小值: 6.函数图形的描绘: 7.曲率 三、教学要求: 1理解并会用罗尔定理,拉格朗日中值定理和泰勒定理: 2.了解并会用柯西中值定理: 3理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的 求法及其简单应用 4.会用导数判断函数的凹凸性,会求函数图形的拐点,会求水平、铅直和斜渐进线,会描绘函数的图形: 5.掌握用罗必达法则未定式极限的方法 6.了解曲率和曲率半径的概念,会计算曲率和曲率半径 四、重点难点 1,重点:罗尔定理,拉格朗日中值定理和泰勒定理的理解与运用,用导数判断函数的单调性凹凸性和 求函数极值以及最值的方法,结合导数知识描绘函数图形:用罗必达法则求未定式极限方法的运用,曲 率和曲率半径的概念及计算 :2.难点:拉格朗日中值定理和泰勒定理的理解与运用;用导数判断函数的单调性,凹凸性和求函数 极值以及最值方法的灵活应用:综合利用导数知识描绘函数图形:罗必达法则的适用条件及类型:曲率 和曲率半径的概念 第一节微分中值定理与导数应用
1 第三章 微分中值定理与导数应用 一、学时分配: 讲课学时:14 习题课学时:2 共 16 学时 二、基本内容: 1.微分中值定理; 2.罗必达法则; 3.泰勒公式; 4.函数单调性与曲线的凹凸性; 5.函数的极值与最大值最小值; 6.函数图形的描绘; 7.曲率. 三、教学要求: 1.理解并会用罗尔定理,拉格朗日中值定理和泰勒定理; 2.了解并会用柯西中值定理; 3.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的 求法及其简单应用; 4.会用导数判断函数的凹凸性,会求函数图形的拐点,会求水平、铅直和斜渐进线,会描绘函数的图形; 5.掌握用罗必达法则未定式极限的方法; 6.了解曲率和曲率半径的概念,会计算曲率和曲率半径. 四、重点难点 1.重点: 罗尔定理,拉格朗日中值定理和泰勒定理的理解与运用; 用导数判断函数的单调性,凹凸性和 求函数极值以及最值的方法; 结合导数知识描绘函数图形;用罗必达法则求未定式极限方法的运用; 曲 率和曲率半径的概念及计算. : 2.难点: 拉格朗日中值定理和泰勒定理的理解与运用; 用导数判断函数的单调性,凹凸性和求函数 极值以及最值方法的灵活应用; 综合利用导数知识描绘函数图形;罗必达法则的适用条件及类型;曲率 和曲率半径的概念. 第一节 微分中值定理与导数应用

教学目的:理解并会用罗尔定理、拉格朗日中值定理,了解柯西中值定理和泰勒中值定理。 教学重点:罗尔定理、拉格朗日中值定理。 教学难点:罗尔定理、拉格朗日中值定理的应用 教学过程: 一、罗尔定理 1.罗尔定理 费马引理设函数f(x)在点x的某邻域U(x,)内有定义,并且在x处可导,如果对任意xEU(,),有 f)sf,)(或fx)2f),那么f(x)=0. 证明:不妨设x∈U(,)时,fx)≤fx)(若f(x)≥f(),可以类似地证明) 于是对于x+AreU,有,+△)≤f化),从而当Ax>0时,区+A-≤0:而当△x<0时, Ar f+△)-f≥0:根据函数f八x)在x,处可导及极限的保号性的得 △Ar 6=fx)=区+As0 △r )=)=-+-f0 Ar 所以fx)=0,证毕。 定义导数等于零的点称为函数的驻点(或稳定点,临界点). 罗尔定理如果函数f)满足:(1)在闭区间[a,b1上连续,(2)在开区间(a,b)内可导,(3)在区间 端点处的函数值相等,即f(@)=f(b),那么在(a,b)内至少在一点S(a<5<b),使得函数fx)在该点的导数 等于零,即f(5)=0 ↑y 2
2 教学目的:理解并会用罗尔定理、拉格朗日中值定理,了解柯西中值定理和泰勒中值定理。 教学重点:罗尔定理、拉格朗日中值定理。 教学难点:罗尔定理、拉格朗日中值定理的应用. 教学过程: 一、罗尔定理 1. 罗尔定理 费马引理 设函数 f (x) 在点 0 x 的某邻域 ( ) 0 U x 内有定义 并且在 0 x 处可导 如果对任意 ( ) 0 xU x 有 ( ) ( ) 0 f x f x (或 ( ) ( ) 0 f x f x ) 那么 ( ) 0 0 ' f x = . 证明:不妨设 ( ) 0 xU x 时, ( ) ( ) 0 f x f x (若 ( ) ( ) 0 f x f x ,可以类似地证明). 于是对于 ( ) 0 0 x + x U x ,有 ( ) ( ) 0 0 f x + x f x , 从而当 x 0 时, 0 ( ) ( ) 0 0 + − x f x x f x ;而当 x 0 时, 0 ( ) ( ) 0 0 + − x f x x f x ;根据函数 f (x) 在 0 x 处可导及极限的保号性的得 0 0 0 0 0 ( ) ( ) ( ) ( ) lim 0 x f x x f x f x f x x + + → + − = = 0 0 0 0 0 ( ) ( ) ( ) ( ) lim 0 x f x x f x f x f x x − − → + − = = 所以 ( ) 0 0 ' f x = , 证毕. 定义 导数等于零的点称为函数的驻点(或稳定点,临界点). 罗尔定理 如果函数 f (x) 满足:(1)在闭区间 [a,b] 上连续 (2)在开区间 (a,b) 内可导 (3)在区间 端点处的函数值相等,即 f (a) = f (b) 那么在 (a,b) 内至少在一点 ( ) a b 使得函数 f (x) 在该点的导数 等于零,即 ' f ( ) 0 = A C B O a y b x

证明:由于f(x)在[a,b]上连续,因此必有最大值M和最小值m,于是有两种可能的情形 (I)M=m,此时fx)在[a,b]上必然取相同的数值M,即fx)=M 由此得f(x)=0.因此,任取5∈(a,b),有f)=0. (2)M>m,由于f)=f),所以M和m至少与一个不等于fx)在区间[a,b]端点处的函数值不妨 设M≠fa)(若m≠fa),可类似证明),则必定在(a,)有一点5使fG)=M.因此任取xe[a,有f)sf() 从而由费马引理有∫'(5)=0.证毕 例1验证罗尔定理对x)=x2-2x-3在区间[-1,3引上的正确性 解显然f(x)=x2-2x-3-(x-3x+)在【-1,3上连续,在(-1,3)上可导,且 f-)=f3)=0,又f"(x)=2(x-1),取5=1,1∈(-1,3》,有f9=0 说明:1若罗尔定理的三个条件中有一个不满足,其结论可能不成立 2使得定理成立的:可能多于一个,也可能只有一个 例如y=中x∈[-2,2]在【-2,2]上除∫0)不存在外,满足罗尔定理的一切条件,但在区间[-2,2】内 找不到一点能使∫"(x)=0 -x,xG(0,除了x=0点不连续外,在[0,川上满足罗尔定理的其余条件,但在区间 例如y={0,x=0 [0,1]上不存在使得f'"(5)=0的点.又如y=x,x∈[0,1小.除了f0)≠f外,在0,]上满足罗尔定理 的其余条仟,但在区间0小上不存在使得了代⑤)=0的点。又如y=c0xX受1请足定理的一 切条件,而5=0,π 2.罗尔定理的应用 罗尔定理1)可用于讨论方程只有一个根:2)可用于证明等式 例2证明方程x心=2在0,内有且仅有一个实根。 证明设f)=xe-2,则f(x)在(-0,+0)内可导。因为f0)<0,f0)>0,根据零点存在定 理,方程xe=2在(0,1)内有一个实根。若方程xe=2在(0,1内至少有两个实根a,b,,则
3 证明:由于 f (x) 在 [a,b] 上连续,因此必有最大值 M 和最小值 m ,于是有两种可能的情形: (1) M = m ,此时 f (x) 在 [a,b] 上必然取相同的数值 M,即 f (x) = M. 由此得 f (x) = 0. 因此,任取 (a,b) ,有 f ( ) 0. = (2) M m ,由于 f (a) = f (b) ,所以 M 和 m 至少与一个不等于 f (x) 在区间 [a,b] 端点处的函数值.不妨 设 M f (a) (若 m f (a),可类似证明),则必定在 (a,b) 有一点 使 f M ( ) = . 因此任取 x [a,b] 有 f x f ( ) ( ) , 从而由费马引理有 f ( ) = 0 . 证毕 例 1 验证罗尔定理对 ( ) 2 3 2 f x = x − x − 在区间 [−1,3] 上的正确性 解 显 然 ( ) 2 3 2 f x = x − x − = (x − 3)(x +1) 在 [−1,3] 上连续,在 (−1,3) 上可导,且 f (−1) = f (3) = 0 , 又 f (x) = 2(x −1), 取 =1, (1(−1,3)) ,有 f ( ) = 0 . 说明:1 若罗尔定理的三个条件中有一个不满足, 其结论可能不成立; 2 使得定理成立的 可能多于一个,也可能只有一个. 例如 y = x , x[−2,2] 在 [−2,2] 上除 f (0) 不存在外,满足罗尔定理的一切条件,但在区间 [−2,2] 内 找不到一点能使 f (x) = 0 . 例如 = − = 0, 0 1 , (0,1] x x x y 除了 x = 0 点不连续外,在 [0,1] 上满足罗尔定理的其余条件,但在区间 [0,1] 上不存在使得 f ( ) = 0 的点.又如 y = x, x[0,1]. 除了 f (0) f (1) 外,在 [0,1] 上满足罗尔定理 的其余条件,但在区间 [0,1] 上不存在使得 f ( ) = 0 的点.又如 ] 2 3 , 2 cos , [ y = x x − 满足定理的一 切条件,而 = 0, 2.罗尔定理的应用 罗尔定理 1)可用于讨论方程只有一个根;2)可用于证明等式. 例 2 证明方程 = 2 x xe 在 (0,1) 内有且仅有一个实根。 证明 设 ( ) = − 2 x f x xe ,则 f (x) 在 (−,+ )内可导。因为 f (0) 0 , f (1) 0 ,根据零点存在定 理,方程 = 2 x xe 在 (0,1) 内有一个实根。若方程 = 2 x xe 在 (0,1) 内至少有两个实根 a,b , 则
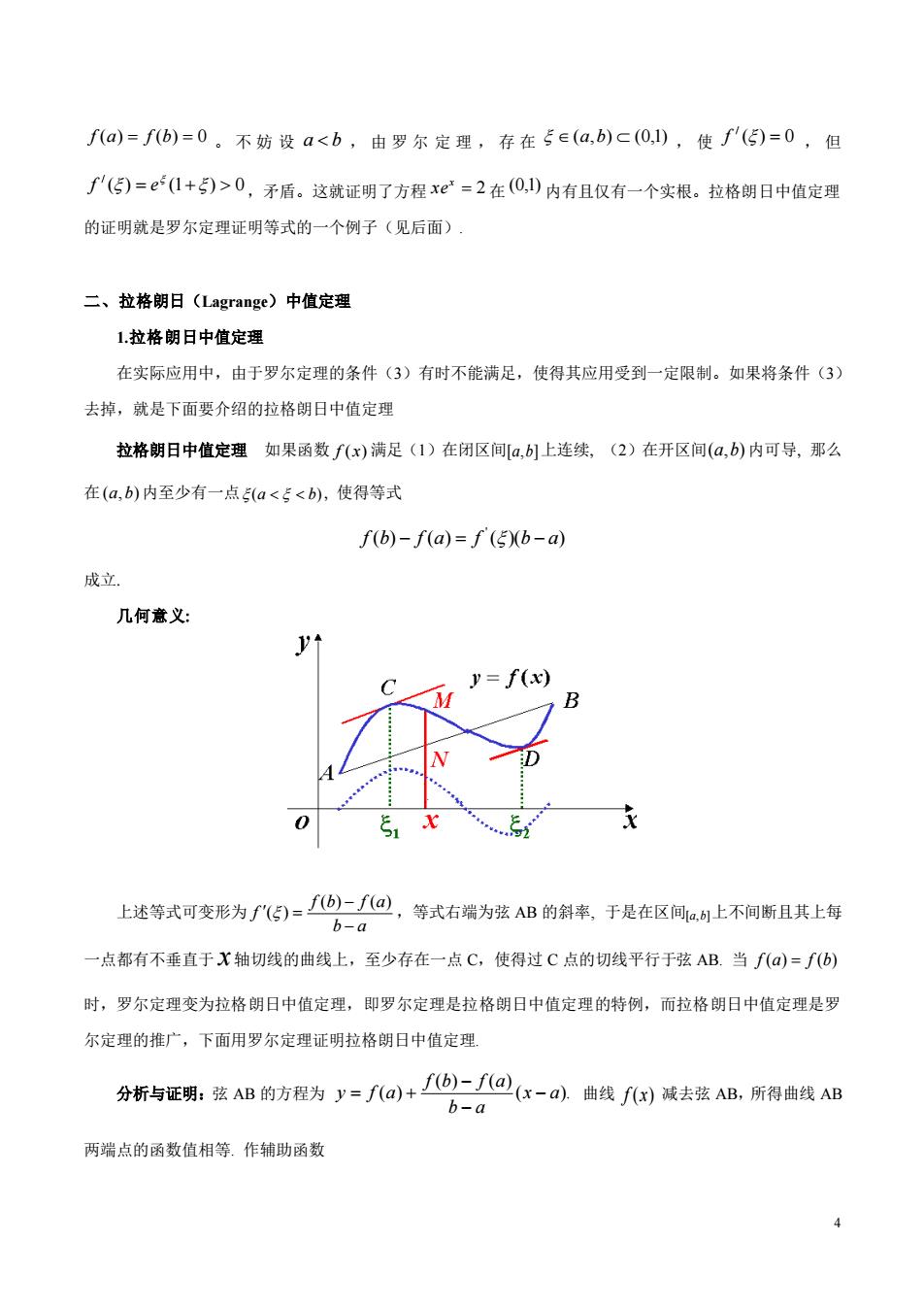
f(a)=f(b)=0。不妨设a<b,由罗尔定理,存在5∈(a,b)c(0,1),使f'()=0,但 '(⑤)=0+)>0,矛盾。这就证明了方程xe=2在(0,)内有且仅有一个实根。拉格朗日中值定理 的证明就是罗尔定理证明等式的一个例子(见后面) 二、拉格朗日(Lagrange)中值定理 1拉格朗日中值定理 在实际应用中,由于罗尔定理的条件(3)有时不能满足,使得其应用受到一定限制。如果将条件(3 去掉,就是下面要介绍的拉格朗日中值定理 拉格朗日中值定理如果函数fx)满足(1)在闭区间[a,1上连续,(2)在开区间(a,b)内可导,那么 在(a,b)内至少有一点a<E<b),使得等式 f(b)-f(a)=f'(5b-a) 成立 几何意义: f(x) 上述等式可变形为∫《们=⑥)-@,等式右端为弦AB的斜率,于是在区间止不间断且其上每 b-a 点都有不垂直于X轴切线的曲线上,至少存在一点C,使得过C点的切线平行于弦AB.当f()-f(b) 时,罗尔定理变为拉格朗日中值定理,即罗尔定理是拉格朗日中值定理的特例,而拉格朗日中值定理是罗 尔定理的推广,下面用罗尔定理证明拉格朗日中值定理 分析与证明:弦AB的方程为y=fa+-/@x-a)曲线f)减去弦AB,所得曲线AB 6-a 两端点的函数值相等.作辅助函数
4 f (a) = f (b) = 0 。 不 妨 设 a b , 由 罗 尔 定 理 , 存 在 (a,b) (0,1) , 使 ( ) 0 / f = , 但 ( ) (1 ) 0 / = + f e ,矛盾。这就证明了方程 = 2 x xe 在 (0,1) 内有且仅有一个实根。拉格朗日中值定理 的证明就是罗尔定理证明等式的一个例子(见后面). 二、拉格朗日(Lagrange)中值定理 1.拉格朗日中值定理 在实际应用中,由于罗尔定理的条件(3)有时不能满足,使得其应用受到一定限制。如果将条件(3) 去掉,就是下面要介绍的拉格朗日中值定理 拉格朗日中值定理 如果函数 f (x) 满足(1)在闭区间 [a,b] 上连续 (2)在开区间 (a,b) 内可导 那么 在 (a,b) 内至少有一点 (a b) 使得等式 ( ) ( ) ( )( ) ' f b − f a = f b − a 成立 几何意义 上述等式可变形为 b a f b f a f − − = ( ) ( ) ( ) ,等式右端为弦 AB 的斜率, 于是在区间 [a,b] 上不间断且其上每 一点都有不垂直于 x 轴切线的曲线上,至少存在一点 C,使得过 C 点的切线平行于弦 AB. 当 f (a) = f (b) 时,罗尔定理变为拉格朗日中值定理,即罗尔定理是拉格朗日中值定理的特例,而拉格朗日中值定理是罗 尔定理的推广,下面用罗尔定理证明拉格朗日中值定理. 分析与证明:弦 AB 的方程为 ( ). ( ) ( ) ( ) x a b a f b f a y f a − − − = + 曲线 f (x) 减去弦 AB,所得曲线 AB 两端点的函数值相等. 作辅助函数

F-u)- 于是F(x)满足罗尔定理的条件,则在(a,b)内至少存在一点5,使得F'(5)=0 又F)=f)-@,所以O=f6)@ b-a b-a 即在(a,b)内至少有一点a<5<b),使得fb)-f(a)=f(⑤b-a).证毕 说明:1.fb)-f(a)=f(5b-a)又称为拉格朗日中值公式(简称拉氏公式),此公式对于b<a也 成立 2.拉氏公式精确地表达了函数在一个区间上的增量与函数在这区间内某点处的导数之间的关系:当设 f(x)在[a,b)上连续,在(a,b)内可导时,若xo,。+△x∈(a,b,则有 fx+△r)-f(x)=f'(x+x)A(0<9<1) 当y=fx)时,也可写成Ay=f"(x。+Ax)Ax(0<B<), 试与微分=∫(x)△x比较:d少=∫"(x)·△x是函数增量△y的近似表达式,而 △y=f"(x。+△x)△x(0<B<I)是函数增量△y的精确表达式.所以拉格朗日中值公式又称为有限增 量公式,拉格朗日中值定理又称有限增量定理 推论若函数在区间1上导数恒为零,则fx)在区间I上是一个常数 2.拉格朗日中值定理的应用 拉格朗日中值定理1)可用于证明等式:2)可用于证明不等式. 例3证明arcsin+arccos=-l≤x≤) 证明:设f(x)=arcsin x+arccosx,xe[-ll] 于京0,所以)Ce-训 1 又f0)=arsn0+acos0=0+7=号,即C=号 放mnx+nosx-号 例4证明恒等式:3arcc0sx-arccos(3x-4r3)=元, 5
5 ( )] ( ) ( ) ( ) ( ) [ ( ) x a b a f b f a F x f x f a − − − = − + 于是 F(x) 满足罗尔定理的条件,则在 (a,b) 内至少存在一点 ,使得 F( ) = 0 . 又 b a f b f a F x f x − − = − ( ) ( ) ( ) ( ) , 所以 b a f b f a f − − = ( ) ( ) ( ) 即在 (a,b) 内至少有一点 (a b) ,使得 ( ) ( ) ( )( ) ' f b − f a = f b − a .证毕 说明: 1. ( ) ( ) ( )( ) ' f b − f a = f b − a 又称为拉格朗日中值公式(简称拉氏公式), 此公式对于 b a 也 成立; 2.拉氏公式精确地表达了函数在一个区间上的增量与函数在这区间内某点处的导数之间的关系;当设 f (x) 在 [a,b] 上连续, 在 (a,b) 内可导时, 若 , ( , ) x0 x0 + x a b , 则有 ( ) ( ) ( ) (0 1) f x0 + x − f x0 = f x0 +x x 当 y = f (x) 时, 也可写成 ( ) (0 1). y = f x0 +x x 试与微分 dy = f (x) x 比较 dy = f (x) x 是函数增量 y 的近似表达式 而 ( ) (0 1) y = f x0 +x x 是函数增量 y 的精确表达式 所以拉格朗日中值公式又称为有限增 量公式, 拉格朗日中值定理又称有限增量定理. 推论 若函数 f (x) 在区间 I 上导数恒为零,则 f (x) 在区间 I 上是一个常数. 2. 拉格朗日中值定理的应用 拉格朗日中值定理 1)可用于证明等式;2)可用于证明不等式. 例 3 证明 ( 1 1) 2 arcsin x + arccos x = − x 证明:设 f (x) = arcsin x + arccos x, x [−1,1] 由于 ) 0 1 1 ( 1 1 ( ) 2 2 = − + − − = x x f x , 所以 f (x) C, x[−1,1] 又 f (0) = arcsin 0 + arccos0 2 0 = + 2 = , 即 2 C = . 故 2 arcsin arccos x + x = . 例 4 证明恒等式: 3arccos − arccos(3 − 4 ) = 3 x x x , − 2 1 , 2 1 x