
由已知的数集有上界,有下界和有界的定义,不难写出函 》1.1雨越 数f(x)在A有上界,有下界和有界的肯定叙述,同时也容是写出 s1.3 第二章极限 它们的否定(即无上界,无下界和无界)叙述现将它们列表对比如下: 522 收敏数列 函数f(x)在A有上界b∈R,∈A,有f()≤b 函数∫(x)在A无上界Vb∈R,3x6∈A,有f(c6)>b 访问主页 函数f()在A有下界 3b∈R,Vx∈A,有f(c)≥a 函数f(a)在A无下界Ha∈R,3xa∈A,有f(xa)<a 标题页 函数∫()在A有界 3M∈R,x∈A,有f(x)川≤M 函数f(x)在A无界 M∈R,3xM∈A,有f(x6>M 显然,函数f(x)在A有上界(有下界)必有无限多个上界(无限多个下界)】 第2页共513页 返回 全屏显示 关闭 退出
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 22 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ❞ ➤ ⑧ ✛ ê ✽ ❦ þ ✳ ➜ ❦ ❡ ✳ Ú ❦ ✳ ✛ ➼ ➶ ➜ Ø ❏ ✕ Ñ ➻ ê f(x) ✸A❦þ✳➜❦❡✳Ú❦✳✛➆➼◗ã➜Ó➒➃◆➫✕Ñ ➜❶✛➘➼(❂➹þ✳➜➹❡✳Ú➹✳)◗ã.②ò➜❶✎▲é✬❳❡: ➻ê f(x) ✸A❦þ✳ ∃ b ∈ R, ∀x ∈ A, ❦f(x) 6 b ➻ê f(x) ✸A➹þ✳ ∀ b ∈ R, ∃xb ∈ A,❦f(xb) > b ➻ê f(x) ✸A❦❡✳ ∃ b ∈ R, ∀x ∈ A, ❦f(x) > a ➻ê f(x) ✸A➹❡✳ ∀ a ∈ R, ∃xa ∈ A, ❦f(xa) < a ➻ê f(x) ✸A❦✳ ∃ M ∈ R, ∀x ∈ A,❦|f(x)| 6 M ➻ê f(x) ✸A➹✳ ∀ M ∈ R, ∃xM ∈ A, ❦|f(xb)| > M ✇✱,➻ê f(x) ✸A❦þ✳(❦❡✳)✼❦➹⑩õ❻þ✳(➹⑩õ❻❡✳)
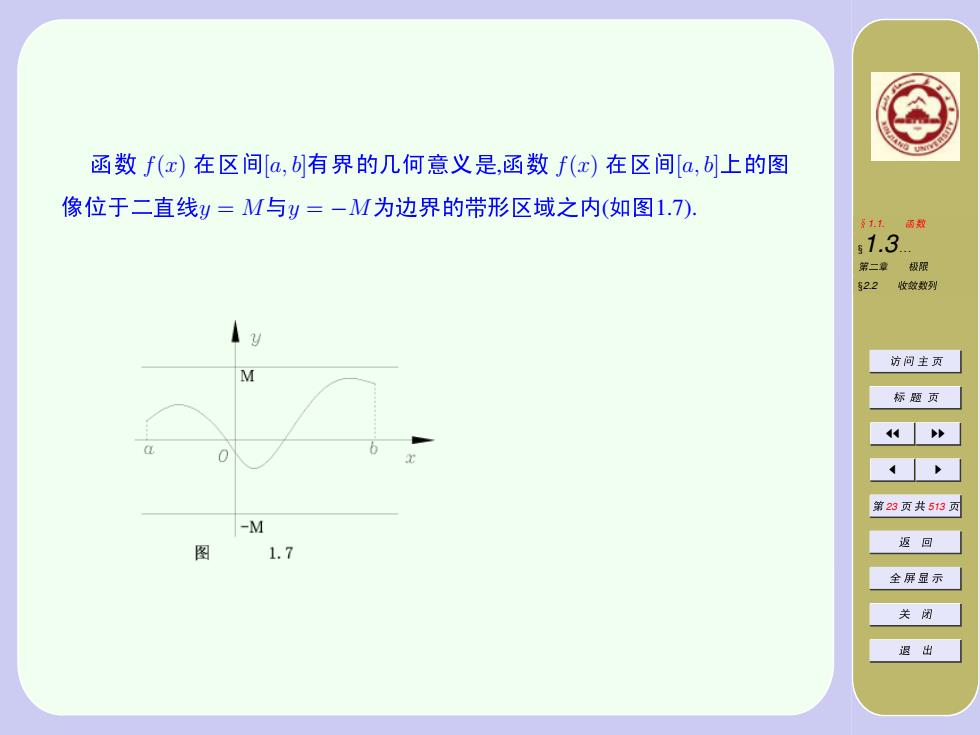
函数f(x)在区间[a,b有界的几何意义是,函数f(x)在区间[a,b1上的图 像位于二直线)=M与y=-M为边界的带形区域之内(如图1.7). 多11雨数 s1.3 第二章极服 $22收敛数列 访问主页 标题页 K 第23页共513页 -M 返回 1.7 全屏显示 关闭 退出
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 23 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ➻ê f(x) ✸➠♠[a, b]❦✳✛❆Û➾➶➫,➻ê f(x) ✸➠♠[a, b]þ✛ã ➈➔✉✓❺❶y = M❺y = −M➃❃✳✛➅✴➠➁❷❙(❳ã1.7)
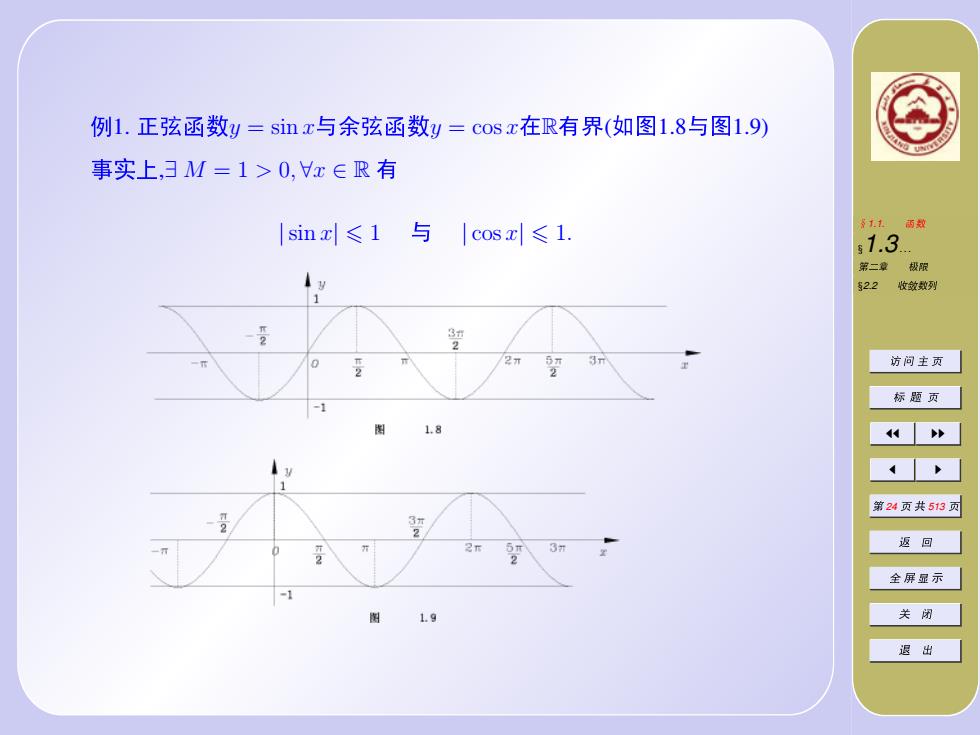
例1.正弦函数y=sinx与余弦函数y=cosx在R有界(如图1.8与图1.9) 事实上,3M=1>0,x∈R有 1 sin≤1与|cosx≤1. 1.1雨越 s1.3. 第二章极限 2.2收敛数列 访问主页 标题页 1.8 炒 第24页共513页 返回 全屏显示 关闭 退出
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 24 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ⑦1. ✔✉➻êy = sin x❺④✉➻êy = cos x✸R❦✳(❳ã1.8❺ã1.9) ➥➣þ,∃ M = 1 > 0, ∀x ∈ R ❦ |sin x| 6 1 ❺ | cos x| 6 1
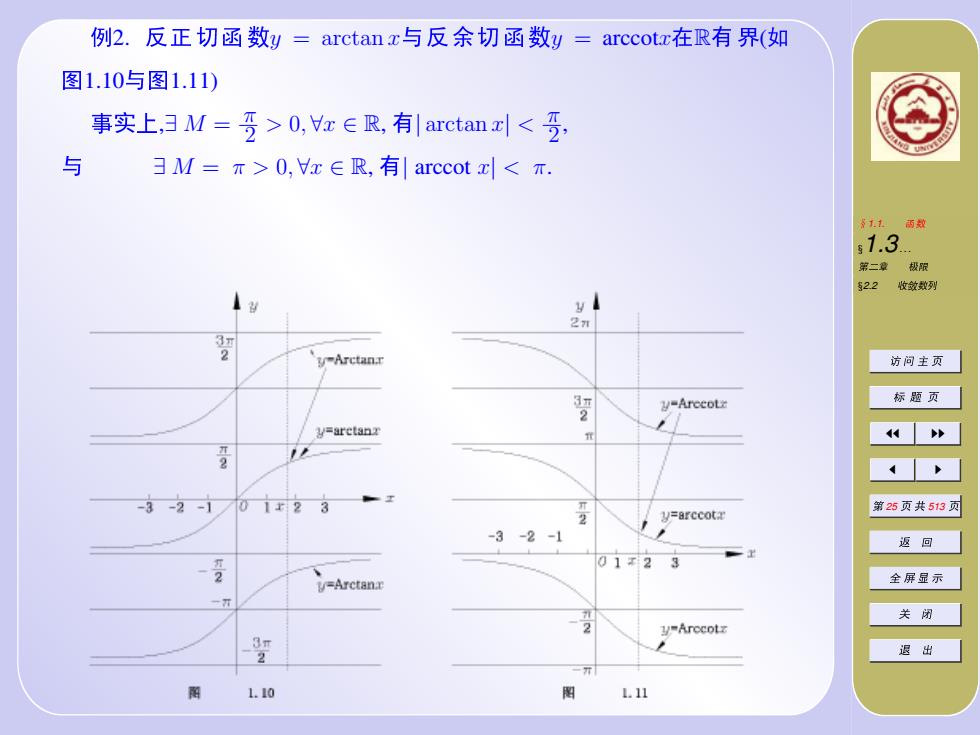
例2.反正切函数y=arctanz与反余切函数y=arccot在R有界(如 图1.10与图1.11) 事实上,3M=>0,z∈R,有|arctan<, 与 3M=π>0,x∈R,有|arccot x<π. 1.1雨数 s1.3 第二章极服 等22收敛数列 2n 2 Arctan.r 访问主页 y-Arccotr 标题页 2 y=arctanx N 3-2-1/0123 y=arccota 第25页共513页 -3-2-1 返回 01x23 V=Arctanx 全屏显示 一开 关闭 y=Arccotz 退出 L.10 L.11
❦1.1. ➻ê §1.3. . . ✶✓Ù ✹⑩ §2.2 ➶ñê✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 25 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ⑦2. ❻✔❷➻êy = arctan x❺❻④❷➻êy = arccotx✸R❦✳(❳ ã1.10❺ã1.11) ➥➣þ,∃ M = π 2 > 0, ∀x ∈ R, ❦| arctan x| < π 2 , ❺ ∃ M = π > 0, ∀x ∈ R, ❦| arccot x| < π

1.1雨数 班.数列+号与{吉}有界 s1.3 第二章极限 事实上,3M=1>0,n∈N,有 $22收敛数列 +y<1 访问主页 标题页 与3M=2>0,neN+,有 炒 m<2 第26页共513页 返回 全屏显示 关闭 退出
❦1.1. ➻ ê §1.3. . . ✶✓Ù ✹ ⑩ §2.2 ➶ ñê ✎ ➊ ➥ ❒ ➄ ■ ❑ ➄ JJ II J I ✶ 26 ➄ ✁ 513 ➄ ❼ ↔ ✜ ➯ ✇ ➠ ✬ ✹ ò Ñ ⑦3. ê ✎ n 1 + ( −1) n+1 2 o ❺ n n + 1 n o ❦ ✳ . ➥➣ þ , ∃ M = 1 > 0 , ∀ n ∈ N + , ❦ 1 + ( −1) n 2 6 1. ❺∃ M = 2 > 0, ∀n ∈ N+, ❦ n + 1 n 6 2