
第五章定积分 一、学时分配: 讲课学时:10习题课学时:2 共12学时 二、基本内容: 1.定积分的概念与性质: 2.微积分基木公式: 5.反常积分的审敛法与「函数。 三、教学要求: 1.理解定积分、反常积分和厂函数的概念及相关性质: 四、重点难点 1.重点:定积分、反常积分和Γ函数的概念:微积分的基本公式以及定积分的换元法 和分部积分法. 2.难点:定积分、反常积分和「函数的相关性质:变动上限的函数的应用:利用微积 分的基本公式以及定积分的换元法和分部积分法求解定积分与反常积分:利 用反常积分的审敛法判断反常积分的敛散性 第一节定积分的概念与性质 教学目的: 1.通过实际问题的引入,使学生理解和掌握定积分的定义与性质: 2.了解定积分的几何意义,能用定积分的定义计算简单的定积分: 3.利用定积分的性质解决估值、证明等相关问题.。 教学重点:定积分的定义. 教学难点:定积分的性质的应用(特别是中值定理). 教学过程: 一、定积分问题举例: 1.曲边梯形的面积 (1)曲边梯形的概念:设y=f(x)在[a,b]上非负,连续.由直线x=a,x=b,y=0 及曲线y=f(x)所围成的图形ABCD称为曲边梯形,其中曲线弧称为曲边 (2)曲边梯形面积的求解 在区间[a,b]中任意插入若干个分点 a=0<x<3<x<xn=b, 把a,b分成n个小区间
第五章 定积分 一、学时分配: 讲课学时:10 习题课学时:2 共 12 学时 二、基本内容: 1.定积分的概念与性质; 2.微积分基本公式; 3.定积分的换元法和分部积分法; 4.反常积分; 5.反常积分的审敛法与 函数. 三、教学要求: 1.理解定积分、反常积分和 函数的概念及相关性质; 2.掌握微积分的基本公式,会利用定积分的换元法和分部积分法求解定积分; 3.掌握反常积分的求解方法,能利用反常积分的审敛法判断反常积分的敛散性. 四、重点难点 1.重点:定积分、反常积分和 函数的概念;微积分的基本公式以及定积分的换元法 和分部积分法. 2.难点:定积分、反常积分和 函数的相关性质;变动上限的函数的应用;利用微积 分的基本公式以及定积分的换元法和分部积分法求解定积分与反常积分;利 用反常积分的审敛法判断反常积分的敛散性. 第一节 定积分的概念与性质 教学目的: 1. 通过实际问题的引入,使学生理解和掌握定积分的定义与性质; 2. 了解定积分的几何意义,能用定积分的定义计算简单的定积分; 3. 利用定积分的性质解决估值、证明等相关问题. 教学重点:定积分的定义. 教学难点:定积分的性质的应用(特别是中值定理). 教学过程: 一、定积分问题举例: 1.曲边梯形的面积 (1)曲边梯形的概念:设 y = f (x) 在 a,b 上非负,连续.由直线 x a = , x b = ,y = 0 及曲线 y = f (x) 所围成的图形 ABCD 称为曲边梯形,其中曲线弧称为曲边. (2)曲边梯形面积的求解 在区间 a,b 中任意插入若干个分点 a = x0 x1 x2 xn−1 xn = b , 把 a,b 分成 n 个小区间 D x o A B C y

[xo][x],[xx] 它们的长度依次为: △x1=x-x0,△x2=x2-x,.,△xn=xn-xn 经过每一个分点作平行于x轴的直线段,把曲边梯形分成n个窄曲边梯形,在每个小区 间[x1x,]上任取一点5:,以[x1,x,]为底,f(5)为高的窄矩形近似替代第i个窄边梯 形(1=1,2,.,n),把这样得到的n个窄矩形面积之和作为所求曲边梯形面积A的近似值, 即 A≈f(5)△x1+f5)△x2+.+f(5n)△x。 =∑f5,)A 设=max{△x1,△x2,.△xn}→0时(这时分段数n无限增多,即n→0),取 上述和式的极限,便得曲边梯形的面积 A=∑fGAx 2.变速直线运动的略程 (1)问题提出:设某物体作直线运动,已知速度v=()是时间间隔[T,T,]上1的连 续函数,且)≥0,计算在这段时间内物体所经过的路程。 (2)解决过程: 在[工,工]内任意插入若干个分点 T=10<1<h2<1n<1n=T2, 把[T,T]分成n个小段 [o],[t,l2],[n1n]。 各小段时间的长依次为: =14-6,△M2=4-4,.,△1n=n-11 相应各段时间内物体经过的路程为:
[ 0 1 x , x ],[ 1 2 x , x ], . [ n n x , x −1 ], 它们的长度依次为: 1 1 0 2 2 1 1 , , , = − = − n = n − n− x x x x x x x x x 经过每一个分点作平行于 x 轴的直线段,把曲边梯形分成 n 个窄曲边梯形,在每个小区 间[ i i x , x −1 ]上任取一点 i ,以[ i i x , x −1 ]为底, ( ) i f 为高的窄矩形近似替代第 i 个窄边梯 形( i n =1, 2, , ),把这样得到的 n 个窄矩形面积之和作为所求曲边梯形面积 A 的近似值, 即 i n n A f ( )x + f ( )x + + f ( )x 1 2 2 = = n i i i f x 1 ( ) 设 = maxx1 ,x2 , xn , → 0 时(这时分段数 n 无限增多,即 n → ),取 上述和式的极限,便得曲边梯形的面积 = → = n i i i A A f x 1 0 lim ( ) 2.变速直线运动的路程 (1)问题提出:设某物体作直线运动,已知速度 v = v(t) 是时间间隔[ 1 2 T ,T ]上 t 的连 续函数,且 v t( ) 0 ,计算在这段时间内物体所经过的路程 s . (2)解决过程: 在[ 1 2 T ,T ]内任意插入若干个分点 1 0 1 2 1 T2 T t t t t t = n− n = , 把[ 1 2 T ,T ]分成 n 个小段 [ 0 1 t ,t ],[ 1 2 t ,t ],., [ n n t ,t −1 ], 各小段时间的长依次为: 1 1 0 2 2 1 1 , , , n n n t t t t t t t t t = − = − = − − . 相应各段时间内物体经过的路程为:

△,△S2,.,△Sn 在[,]上任取一个时刻x,(≤T,≤1,),以x,时的速度(c)来代替[,]上各个 时刻的速度,则得:△心≈(c)山0=1,2,.,n) 进一步得到:3≈(c)△+)山,++Wr)△n=∑(c,)△ 设=mx4,A4,M}当元→0时,得:5=lm∑g,AM 二、定积分的定义 1.问题总结:由上述两例可见,虽然所计算的量不同,但它们都决定于一个函数及其 自变量的变化区间,其次它们的计算方法与步骤都相同,即归纳为一种和式极限,即 面积A=m∑f传)△x, 路程S=m∑T)△4,· 将这种方法加以概括,就可以抽象出下述定积分的定义。 2.定积分的定义设函数f(x)在[a,b)上有界,在[a,b]中任意插入若干个分点 a=X0<1<x2<.<xm-1<xn=b 把区间[a,b分成n个小区间 [x0,x][x,x2].,[xn-,xn] 各个小区间的长度依次为△x1=X-x0,△x2=x2-x,.,△xn=xn一X 在每个小区间[xx,]上任取一点5(≤≤x),作函数值f()与小区间长度A,的 乘积f(5)△x(=1,2,.,n),并作出和 S=∑fE)△x (1) 记元=max{△x,△x2,△xn,如果不论对[a,b怎样分法,也不论在小区间[x-1,x,]上点 怎样取法,只要当入→0时,和S总趋于确定的极限1,这时我们称这个极限I为函数
1 2 , , , n s s s . 在[ i i t ,t −1 ]上任取一个时刻 1 ( ) i i i i t t − ,以 i 时的速度 ( )i v 来代替[ i i t ,t −1 ]上各个 时刻的速度,则得: ( ) i i i s v t (i = 1,2, ,n) 进一步得到: 1 1 2 2 ( ) ( ) ( ) n n s v t v t v t + + + 1 ( ) n i i i v t = = . 设 = maxt 1 ,t 2 , ,t n ,当 → 0 时,得: 0 1 lim ( ) n i i i s v t → = = . 二、定积分的定义 1.问题总结:由上述两例可见,虽然所计算的量不同,但它们都决定于一个函数及其 自变量的变化区间,其次它们的计算方法与步骤都相同,即归纳为一种和式极限,即 面积 = → = n i i i A f x 1 0 lim ( ) , 路程 = → = n i i i S v T t 1 0 lim ( ) . 将这种方法加以概括,就可以抽象出下述定积分的定义. 2.定积分的定义 设函数 f x( ) 在 [ , ] a b 上有界,在 [ , ] a b 中任意插入若干个分点 a = x0 x1 x2 xn−1 xn = b 把区间 a,b 分成 n 个小区间 [ , ],[ , ], ,[ , ], 0 1 1 2 n 1 n x x x x x x − 各个小区间的长度依次为 1 1 0 2 2 1 1 , , , = − = − n = n − n− x x x x x x x x x . 在每个小区间[ i i x , x −1 ]上任取一点 1 ( i i i i x x − ),作函数值 ( )i f 与小区间长度 i x 的 乘积 ( ) ( 1,2, , ), i i f x i n = 并作出和 1 ( ) n i i i S f x = = . (1) 记 max{ , , , } 1 2 n = x x x ,如果不论对 a,b 怎样分法,也不论在小区间[ i i x , x −1 ]上点 i 怎样取法,只要当 →0 时,和 S 总趋于确定的极限 I ,这时我们称这个极限 I 为函数

fx)在区间[a,b上的定积分(简称积分),记作fx)dx,即 (dx=1m(Ax. (2) 其中fx)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分变量,a叫做积分下限,b 叫做积分上限,[a,b叫做积分区间. 利用“6-6”的说法,上述定积分的定义可以表述如下: 设有常数1,如果对于任意给定的正数6总,存在一个正数δ,使得对于区间[4,b]的 任何分法,也不论三,在[x1,x,]中怎样取法,只要入<6,总有 I∑fG)Ax-1kE 成立,则称I是fx)在区间a,b上的定积分,记作∫fx)dx。 注意:1.当和∑f(5,)△x,的极限存在时,其极限I仅与被积函数f(x)及积分区间 [a,有关。 2,积分与积分变量的记法无关,即: ∫fx)dx=f)d1=∫f)du 3.S=立八G,A通常称为积分和.如果f)在区间血,)上的定积分存在,则说 fx)在[a,b上可积. 3.函数可积的两个充分条件 定理1设f(x)在a,b]上连续,则fx)在[a,b上可积. 定理2设f(x)a,b]上有界,且只有有限个间断点,则f(x)a,b]上可积. 4.定积分的几何意义 由前面的讨论知,当f(x)≥0时,函数f(x)在[a,b]的定积分」fx)dx在几何上表 示由曲线由直线x=a,x=b,y=0及曲线y=∫(x)所围成的曲边梯形的面积
f (x) 在区间 a,b 上的定积分(简称积分), 记作 ( )d b a f x x ,即 ( )d b a f x x = I = 0 1 lim ( ) n i i i f x → = , (2) 其中 f (x) 叫做被积函数, f x x ( )d 叫做被积表达式, x 叫做积分变量, a 叫做积分下限, b 叫做积分上限, a,b 叫做积分区间. 利用“ − ”的说法,上述定积分的定义可以表述如下: 设有常数 I ,如果对于任意给定的正数 总,存在一个正数 ,使得对于区间 a,b 的 任何分法,也不论 i 在[ i i x , x −1 ]中怎样取法,只要 ,总有 1 | ( ) | n i i i f x I = − 成立,则称 I 是 f (x) 在区间 a,b 上的定积分,记作 ( )d b a f x x . 注意:1.当和 1 ( ) n i i i f x = 的极限存在时,其极限 I 仅与被积函数 f (x) 及积分区间 a,b 有关. 2.积分与积分变量的记法无关,即: ( )d ( )d ( )d b b b a a a f x x f t t f u u = = . 3. 1 ( ) n i i i S f x = = 通常称为积分和.如果 f (x) 在区间 a,b 上的定积分存在,则说 f (x) 在 a,b 上可积. 3.函数可积的两个充分条件 定理 1 设 f (x)在[a,b] 上连续,则 f (x) 在 a,b 上可积. 定理 2 设 f (x)在[a,b] 上有界,且只有有限个间断点,则 f (x)在[a,b] 上可积. 4.定积分的几何意义 由前面的讨论知,当 f x( ) 0 时,函数 f (x)在[a,b] 的定积分 ( )d b a f x x 在几何上表 示由曲线由直线 x a = , x b = , y = 0 及曲线 y = f (x) 所围成的曲边梯形的面积.
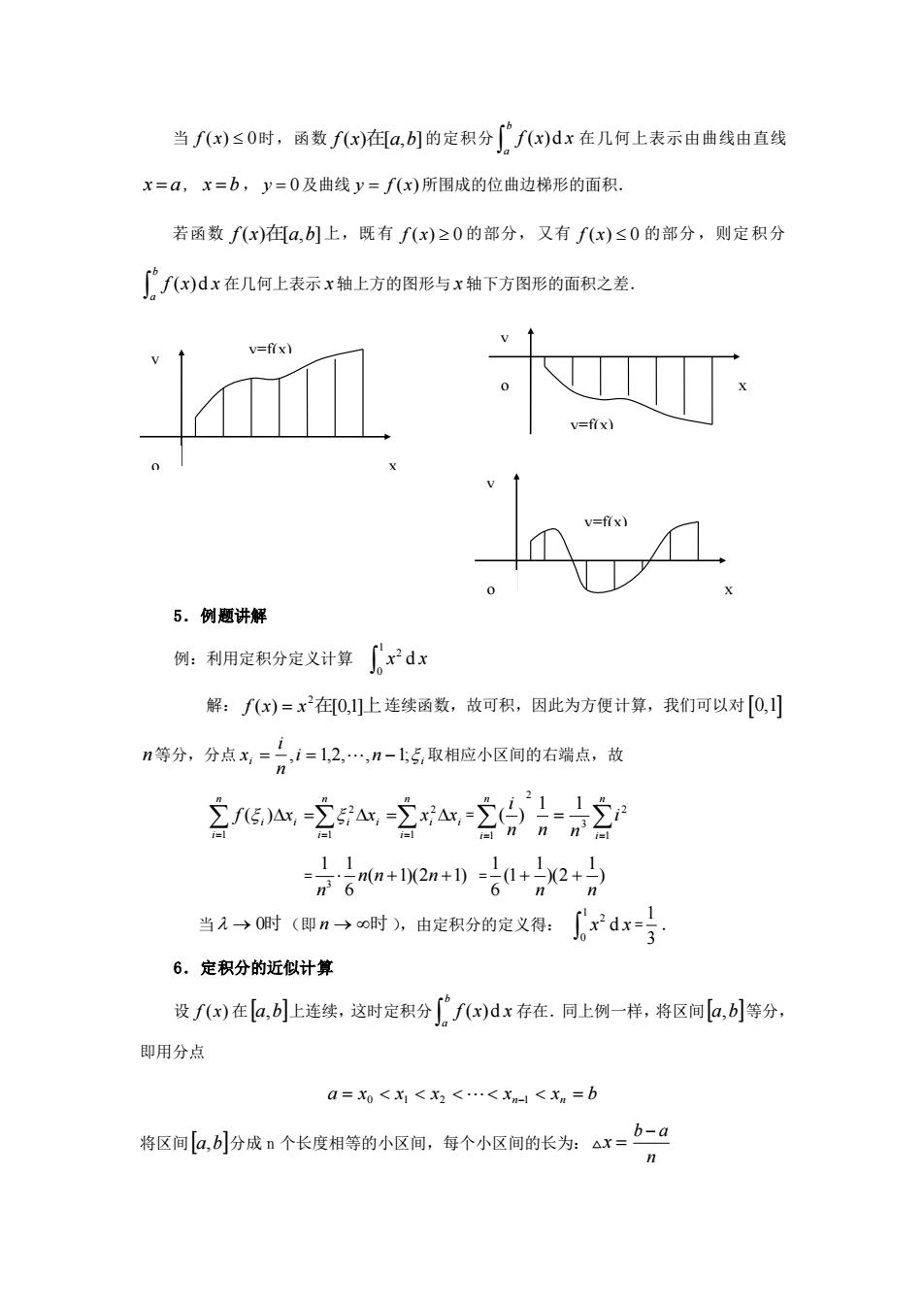
当fx)≤0时,函数fx)在a,的定积分[fx)dx在几何上表示由曲线由直线 x=a,x=b,y=0及曲线y=fx)所围成的位曲边梯形的面积 若函数f(x)a,b]上,既有f(x)≥0的部分,又有f(x)≤0的部分,则定积分 ∫f(x)dx在几何上表示x轴上方的图形与x轴下方图形的面积之差, v↑ v=fix =frx) v=f7x) 5.例题讲解 例:利用定积分定义计算[x2dx 解:fx)=x在0,止连续函数,故可积,因此为方便计算,我们可以对[0, n等分,分点x,=。i=12,.,1-上5,取相应小区间的右端点,故 5宫9- 名a+2m+)0+x2+的 当无→0时(即n→时),由定积分的定义得:rdx背 6.定积分的近似计算 设f(x)在[a,b上连续,这时定积分f(x)dx存在.同上例一样,将区间a,b等分, 即用分点 a=0<x<3<.<x<xn=b 将区间血,小分成n个长度相等的小区间,每个小区间的长为△x=-口
当 f x( ) 0 时,函数 f (x)在[a,b] 的定积分 ( )d b a f x x 在几何上表示由曲线由直线 x a = , x b = , y = 0 及曲线 y = f (x) 所围成的位曲边梯形的面积. 若函数 f (x)在[a,b] 上,既有 f x( ) 0 的部分,又有 f x( ) 0 的部分,则定积分 ( )d b a f x x 在几何上表示 x 轴上方的图形与 x 轴下方图形的面积之差. 5.例题讲解 例:利用定积分定义计算 1 2 0 x x d 解: f (x) = x 2在[0,1]上 连续函数,故可积,因此为方便计算,我们可以对 0,1 n 等分,分点 i n i i n i x = , = 1,2,, −1; 取相应小区间的右端点,故 = = = = = n i i i n i i i n i i i f x x x x 1 2 1 2 1 ( ) = = = = n i n i i n n n i 1 2 3 2 1 1 1 ( ) = 3 1 1 ( 1)(2 1) 6 n n n n + + = ) 1 )(2 1 (1 6 1 n n + + 当 → 0时 (即 n → 时 ),由定积分的定义得: 1 2 0 x x d = 3 1 . 6.定积分的近似计算 设 f (x) 在 a,b 上连续,这时定积分 ( )d b a f x x 存在.同上例一样,将区间 a,b 等分, 即用分点 a = x0 x1 x2 xn−1 xn = b 将区间 a,b 分成 n 个长度相等的小区间,每个小区间的长为: x = b a n − y=f(x) o x y o x y y=f(x) y=f(x) o x y