
为波尔半径。 氢原子总能量品,应为其动能(合m和势能(仁层R )之总和,即 E=moe+(-g)》 将(1-1.13)(1-1.15)代入即得氢原子的总能量E (1-1.16) 其中 R=2zime=13.6cV 2 (1-1.17) 当n=1时,E=-R=-13.6eV,即为氢原子基态能量。相应 于量子数=1,2,3,.诸定态的能量为一R,一R/4,一R/9,.等 等,分别为各激发态的能量。当原子在定态1和定态2间跃迁 时,放出或吸收的辐射,其频率即为: 加=Be-B=R得) 故 (1-1.18) 于是 ia=是-2m0-109737cm (1-1.19) 可见,根据波尔理论计算而得的里德伯常数H和实验值基本上 是一致的。由于电子实际上不是绕核而是绕着整个体系的质心而 运动,故若以约化质量A=nn(a和M分别为电子和原子核 的质量)代替上述公式中的m,(约化质量又称折合质量),将可得 到非常符合于实验值的结果。(参看§1-6,图1-6.1) Bohr理论虽然成功地解释了氢原子光谱,但若用它进一步来 研究氢光谱的精细结构和多电子原子的光谱现象,就遇到无法克 ·15· 仅限读者PB18030910本人使用,阅华请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

服的矛盾。对干原子为什么能够稳定存在的原因也未能作出满意 的解释。因为它木质上仍然属于经典力学范畴,只不过附加上一 些人为的量子化杀件,也没有建立这种量子化条件和电子本性及 其运动现象之间的联系,所以称之为旧的量子理论,有待进一步发 展,而这个发展首先要基于对电子等实物微粒本性的认识。 §1-2实物微粒的波动性 1.从光子说到物质波: 爱因斯坦在1905年提出的光子说成功地解释了光电效应这 一事实,迫使人们第一次不得不对同一客体使用两种图象来描述: 即光虽然确定是一种电磁波,但同时亦是一束由光子组成的微粒 流。振动频率为y的光的每一光子不单具有能量(E=),而且 还具有动量(p=/2),表征微粒性的量E和卫与表征波动性的量 ”和入又通过普朗克常数h定量地联系起来。可是另一方面,它 具粒性,又不服从经典的牛顿(Newton)定律(例如光在真空中运 动速度是一常数,永远为¢,所以加速度对它根本没有意义),也没 有经典的运动轨道。它呈现波动性,遵从麦克斯威(Maxwell)的电 磁场方程,但又不是经典意义下的波,它的波动场具量子化,且表 现有一种统计的规律性:即在某一时刻空间某处单位体积内出现 光子的数目(对大量光子面言)或一个光子在某处出现的几率(对 一个光子而言)是与该处的光强(正比于经典电磁理论中电场和磁 场强度的平方)成正比,出现时必是整个光子,而不能是一个光子 的一个部分。 其次,虽然光是微粒和波动的矛盾统一体,但在不同场合下, 可以侧重于一个方面的性质。在光的发射过程中,或在与实物相 互作用时,光的微粒性表现较突出,因此有关原子光谱,光电效应、 黑体辐射等现象就要从微粒观点来解释;而当光在空间传播时, ·16· 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

就要从波动观点来解释有关光的偏振、干涉和衍射等现象。也就 是说,光的微粒性和波动性既互相渗透又相互转化。 到了1923年前后,玻尔原子结构理论一方面取得了很大的成 功,但却同时遇到了极其严重的困难。很多物理学家都在为探索 发展玻尔原子结构理论的道路而作出努力,其中有唯物论思想倾 向的法国年青物理学家德布罗意(L·de Broglie)就是一个杰出 的代表。他在光的波粒二象性思想的启发下,指出:“几个世纪以 来,在光学方面,人们过于重视波动的研究方法,而过于忽视粒子 的研究方法;在实物的理论(例如原子结构理论)方面,是否犯了 相反的错误呢?是否我们过多地围绕着粒子的图象作思考,却过分 地忽视了波的图象?”于是,他大胆地提出了久已被认为由粒子构 成的物质,其实却必定伴随有波,从而带有波的性质。并且提出适 合于光的两个著名关系式也同样适合于电子等实物微粒,即 B=m,卫=受 (1-2.1) 这就是说,实物微粒和辐射一样,其总能量E和动量P以及伴 随它运动的波的频率”和波长入也可以由一个普适常数飞定量地 联系起来。一定的物质微粒流将有相应的物质波控制它的运动, 正如辐射的光量子流有一个波伴随着而控制它的运动一样。 对于一个质量为m,运动速度为)的实物微粒,其动量卫= mv,故上式又可写成 A=合-品 (1-2.2) 这种形式又叫做德布罗意关系式。它预示着物质波的波长,可以 通过实物微粒的大小及其运动速度来衡量。对于宏观物体而言, 由于物质波长很短,通常不会显出其波性的。对于微观粒子而言, 虽入的大小和微粒本身的线度、质量、电荷等可以比拟,但其数量 级仍很小,因此可以理解,这种物质波的假设开始时很难被人们所 ·17· 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播

接受。可是,爱因斯坦却立刻看出它可能有的重要性,并拿自己非 同小可的声誉作了它的后盾。这种假定的提出就为发展玻尔原子 结构理论以及建立量子力学理论,开辟了前进的道路。 2.物质波的实验证明: 1927年,德布罗意的假设分别被戴维逊-革末(C.·Davisson -L·H·Germer)的电子束在镍单晶上反射以及汤姆逊(G.P. Thomson)的电子衍射实验所证实。 如图1-2.1所示,戴维逊-革末发现,当一束54eV的电子垂 采测 图1-2.1戴维逊-草术实验示意 直地射在镍单晶表面上时,在和入射束成p=50°角的方向上表现 有反射出来最多的电子数。这类似于X-射线在晶体表面上反射 时所产生的衍射图象。假定只考虑衍射图象的第一级极大,则在 两相邻晶面中的原子所衍射电子射线的光程差正好等于入射电子 波波长1(如图1-2.2所示): 2=2d3in6 (1-2.3) 式中0为半衍射角,0=号(红一m)=65°,d为镍原子晶面间距,由 X-射线衍射法可测得d=0.91A,故可算得元=1.65。另一方面, ·18· 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播
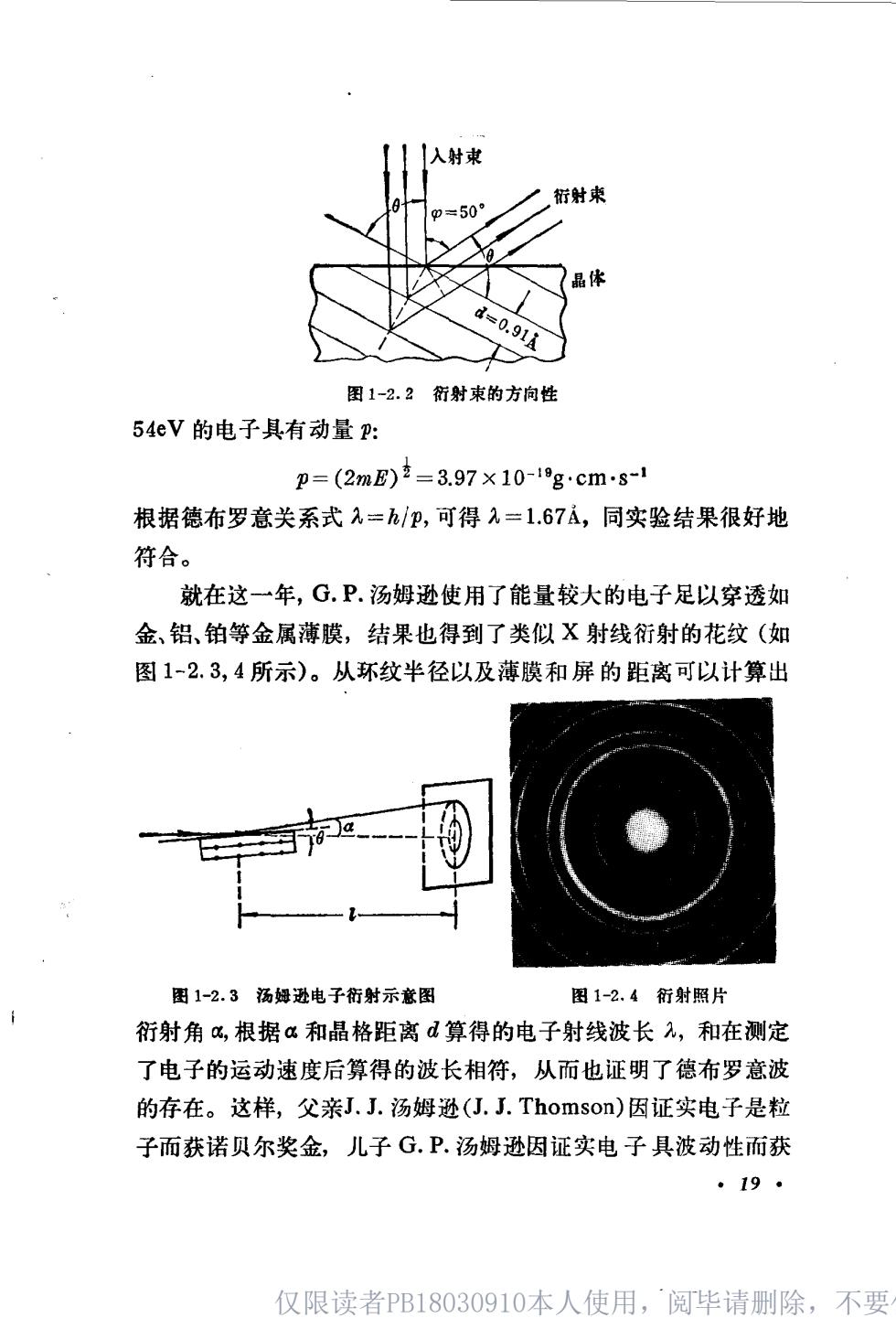
图1-2.2衍射束的方向性 54eV的电子具有动量p: p=(2mE)克=3.97×10-1g·cm81 根据德布罗意关系式入=h/P,可得1=1.67A,同实验结果很好地 符合。 就在这一年,G.P.汤姆逊使用了能量较大的电子足以穿透如 金、铝、铂等金属薄膜,结果也得到了类似X射线衍射的花纹(如 图1-2.3,4所示)。从环纹半径以及薄膜和屏的距离可以计算出 图1-2.3汤姆逊电子衍射示意图 图1-2.4衍射照片 衍射角%,根据a和晶格距离d算得的电子射线波长,和在测定 了电子的运动速度后算得的波长相符,从而也证明了德布罗意波 的存在。这样,父亲J.J.汤姆逊(J.J.Thomson)因证实电子是粒 子而获诺贝尔奖金,儿子G.P.汤姆逊因证实电子具波动性而获 。19· 仅限读者PB18030910本人使用,阅毕请删除,不要
仅限读者PB18030910本人使用,阅毕请删除,不要传播