
回复动力学特点: (1)回复过程没有孕育期,随着退火的开始 进行,发生软化。 (2)在一定温度下,初期的回复速率很大, 以后逐渐变慢,直到最后回复速率为零。 (3)每一温度的回复程度有一极限值,退火 温度越高,这个极限值也越高,而达到此极 限所需时间则越短 (4)回复不能使金属性能恢复到冷变形前的 水平。 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 回复动力学特点: (1)回复过程没有孕育期,随着退火的开始 进行,发生软化。 (2)在一定温度下,初期的回复速率很大, 以后逐渐变慢,直到最后回复速率为零。 (3)每一温度的回复程度有一极限值,退火 温度越高,这个极限值也越高,而达到此极 限所需时间则越短 (4)回复不能使金属性能恢复到冷变形前的 水平

2.回复动力学方程 设P为冷变形后在回复阶段发生变化的某种性能,如临界切应 力,Po为变形前该性能的值,△P=P-P为加工硬化造成的该性能的 增量,与晶体中晶体缺陷的体积浓度C成正比。 P-Po=△P=KCp (1) : 将(1)式对时间t求导,得出Cp与P随时间的变化率为: (2) dt 缺陷的变化是一个热激活的过程,设激活能为Q,仿照化学动力 学的方法,对一级反应,反应速度与浓度的一次方成比例 dt 则(2)式变为: dt 将(1)式代入: d(P-B)=-k. 海南大学材科科学与工程基础电子,柰 K RT
海南大学材料科学与工程基础电子教案 2.回复动力学方程 设P为冷变形后在回复阶段发生变化的某种性能,如临界切应 力,P0为变形前该性能的值,ΔP=P-P0为加工硬化造成的该性能的 增量,与晶体中晶体缺陷的体积浓度CP成正比。 P-P0=ΔP=K CP (1) 将(1)式对时间t求导,得出CP与P随时间的变化率为: ( 2 ) 缺陷的变化是一个热激活的过程,设激活能为Q,仿照化学动力 学的方法,对一级反应,反应速度与浓度的一次方成比例 dt dC K dt d P P P = ( − ) 0 = − − RT Q AC dt dC P P exp 则(2)式变为: 将(1)式代入: = − − − RT Q Kc A dt d P P P exp ( ) 0 − − = − − RT Q A K P P K dt d P P exp ( ) 0 0

积分得: -4号 P-Po (3) n-Ae号}C (4) 由(4)式得出:回复阶段性能随时间而衰减,服从指数规律。 如果采用两个不同的温度将同一冷变形金属的性能回复到同样 的程度,则 exp t一 exp RT 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 积分得: (3) (4) 由(4)式得出:回复阶段性能随时间而衰减,服从指数规律。 dt RT Q A P P d P P = − − − − exp ( ) 0 0 t C RT Q P P A + ln( − 0 ) = − exp − 如果采用两个不同的温度将同一冷变形金属的性能回复到同样 的程度,则 2 2 1 1 exp exp t RT Q t A RT Q A = − − − − = − − = 2 1 1 1 1 2 2 1 exp exp R T T e RT RT t t
■屈服强度的回复动力学 与以上公式相符 ■没有孕育期; 0.8 300C 350°C ·开始变化快,随后变慢; 0.6 400℃ ·长时间处理后,性能趋 0.4 450C 于一平衡值。 0.2 500c 实验证明,Q与空位的 50100150200250300350400450 扩散激活能十分接近, 时间/min 图8-34经拉伸变形的纯铁在不同温度下 说明回复过程主要是由 加热时,屈服强度的回复动力学 空位扩散实现的
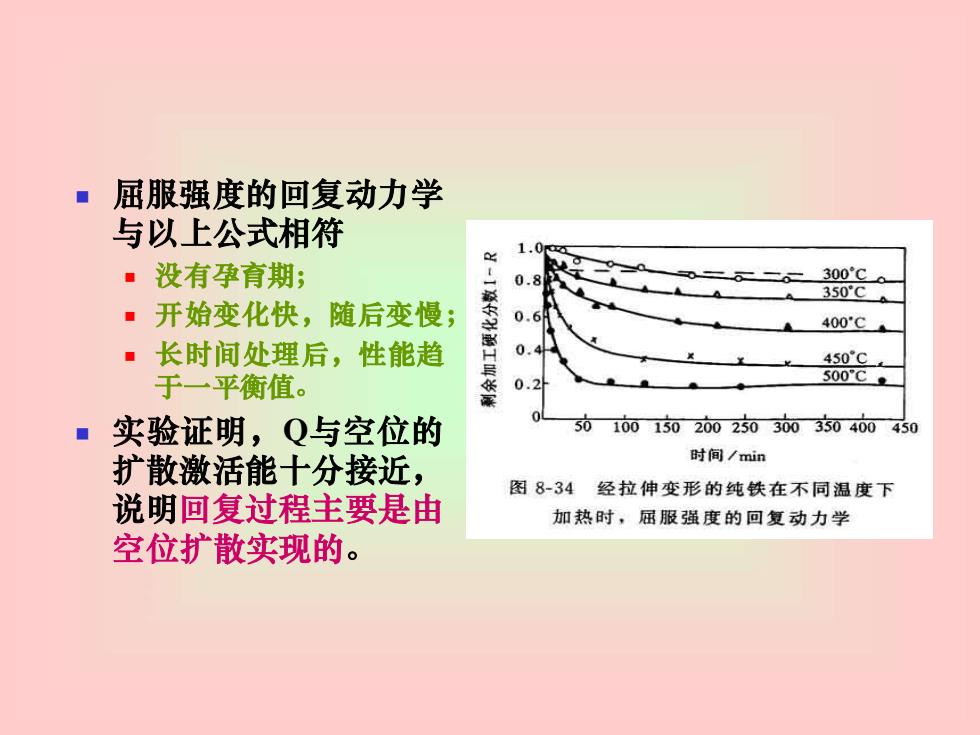
◼ 屈服强度的回复动力学 与以上公式相符 ◼ 没有孕育期; ◼ 开始变化快,随后变慢; ◼ 长时间处理后,性能趋 于一平衡值。 ◼ 实验证明,Q与空位的 扩散激活能十分接近, 说明回复过程主要是由 空位扩散实现的

回复动力学方程 例:已知锌单晶的回复激活能Q=20000cal/mol,在0℃回复到 残留75%的加工硬化需5min,请问在27℃和-50℃回复到同样 程度需多长时间? 20000×4.180 1 解:t1=5e 8.31 273300 =0.185(min) 20000x4.1811 t,=5e 8.31 273223 =18500min≈13(天) 测量出几个不同温度下回复到相同P值所需的时间,利用 (4)式并取对数,得到: ht-常数+ RT 从nt-T 关系可求出激活能,利用Q以推断可能的回复机制。 海南大学材料科学与工程基础电子教案
海南大学材料科学与工程基础电子教案 回复动力学方程 例:已知锌单晶的回复激活能Q=20000cal/mol,在0℃回复到 残留75%的加工硬化需5min,请问在27℃和-50℃回复到同样 程度需多长时间? 解: (min) min≈13(天) 测量出几个不同温度下回复到相同P值所需的时间,利用 (4)式并取对数,得到: 从 关系可求出激活能,利用Q以推断可能的回复机制。 5 18500 223 1 273 1 8.3 1 20000 4.1 8 2 = = − − t e 5 0.185 300 1 273 1 8.31 20000 4.18 1 = = − − t e RT Q ln t = 常数 + T t 1 ln −