§6.3轴心受压构件的整体稳定 二、临界应力的确定 1.理想构件的弹性弯曲失稳 理想条件:绝对直杆、材料均质、无荷载偏心、 无初始应力、完全弹性。 d2y1-_」 M d2 El 剪力V产生的轴线转角为: r=B B dM M=N.y d GA GA dz 可列平衡方程 -》-
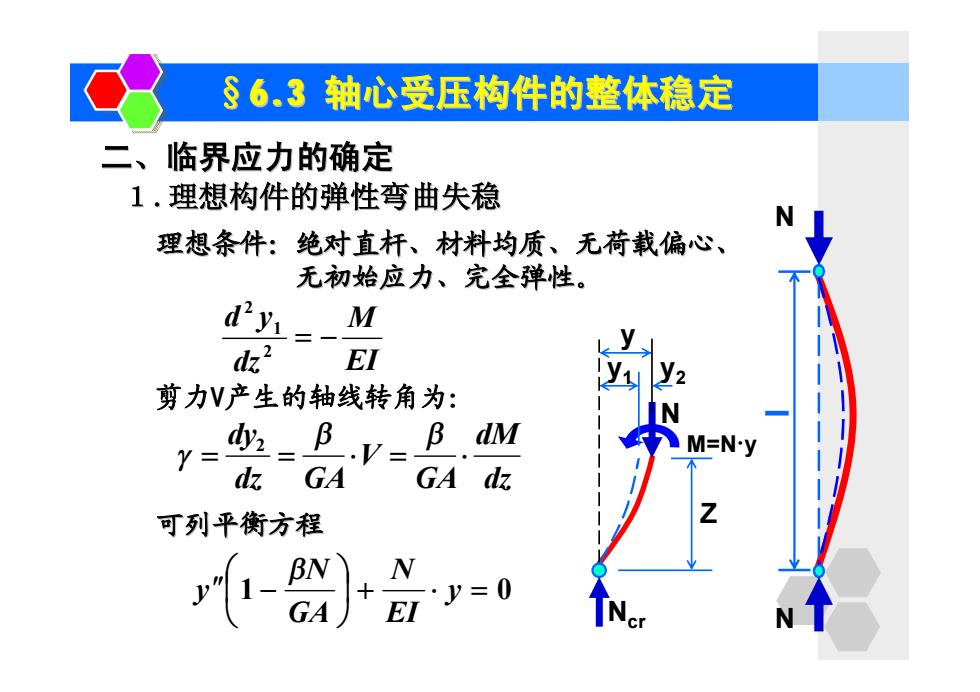
可列平衡方程 二、临界应力的确定 理想条件:绝对直杆、材料均质、无荷载偏心、 无初始应力、完全弹性。 §6.3 轴心受压构件的整体稳定 1.理想构件的弹性弯曲失稳 N N l y y1 y2 Ncr N M=N·y Z 1 ÷ + × = 0 ø ö ç è æ ¢¢ - y EI N GA N y b EI M dz d y = - 2 1 2 剪力V产生的轴线转角为: dz dM GA V dz GA dy = = × = × b b g 2
§6.3轴心受压构件的整体稳定 二、临界应力的确定 1.理想构件的弹性弯曲失稳 通常剪切变形的影响较 NE=T'EI 小,可忽略不计,即得欧拉 1 21+元2E. 临界力和临界应力: GA π2El 元2EA 1 NE 0E= A22 ,π2EAB 1+ 22 GA 元2E 22
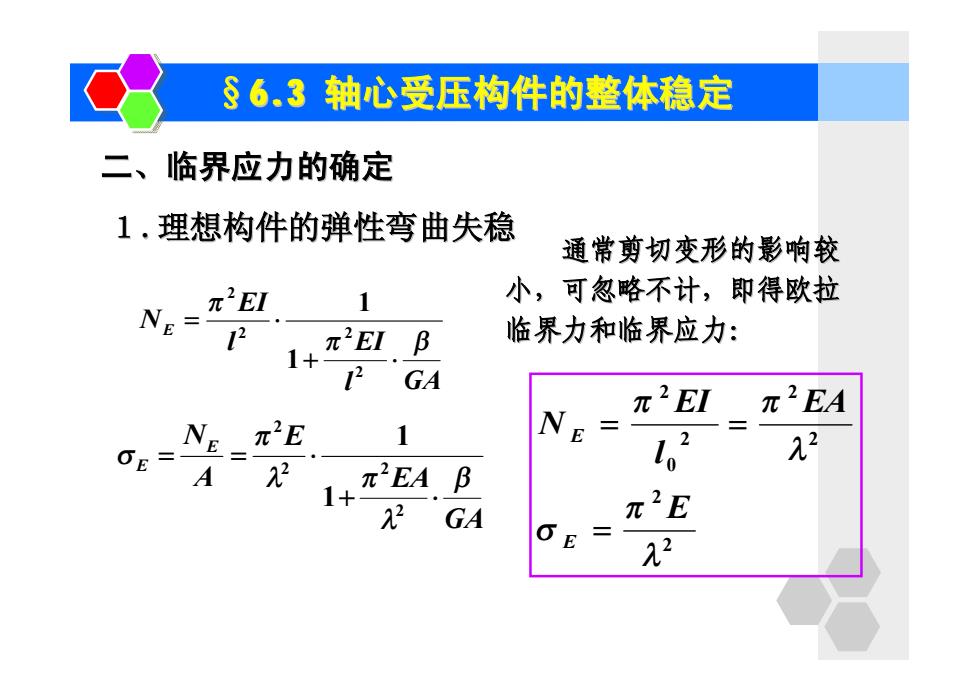
二、临界应力的确定 §6.3 轴心受压构件的整体稳定 1.理想构件的弹性弯曲失稳 l GA l EI EI NE p b p + × = × 2 2 2 2 1 1 GA EA E A NE E b l l p p s + × = = × 2 2 2 2 1 1 2 2 2 2 2 0 2 l p s l p p E EA l EI N E E = = = 通常剪切变形的影响较 小,可忽略不计,即得欧拉 临界力和临界应力:
§6.3轴心受压构件的整体稳定 二、临界应力的确定 2.理想构件的弹塑性弯曲失稳 构件失稳时如果截面应力 E:旷 超出弹性极限,则构件进入弹 塑性工作阶段,这时应按切线 模量理论进行分析: p N 元2E,I π2E. 22
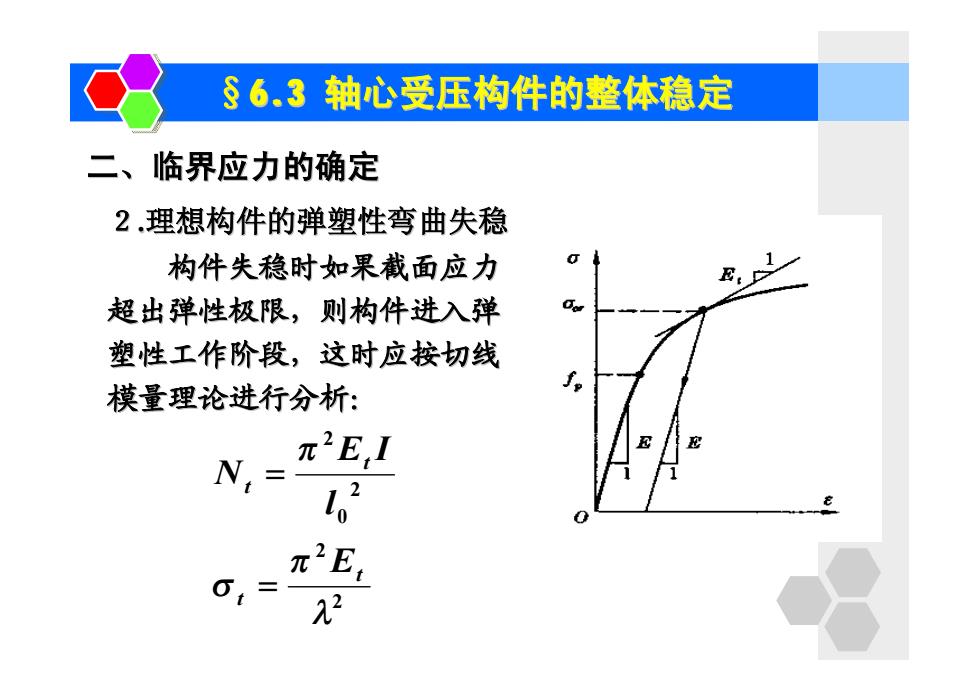
2.理想构件的弹塑性弯曲失稳 构件失稳时如果截面应力 超出弹性极限,则构件进入弹 塑性工作阶段,这时应按切线 模量理论进行分析: 二、临界应力的确定 §6.3 轴心受压构件的整体稳定 2 2 2 0 2 l p s p t t t t E l E I N = =
§6.3轴心受压构件的整体稳定 二、 临界应力的确定 切线模量理论0Gr-t 轴压构件 歌拉双曲线G=E 临界应力与入 的关系曲线, 称为柱子曲线
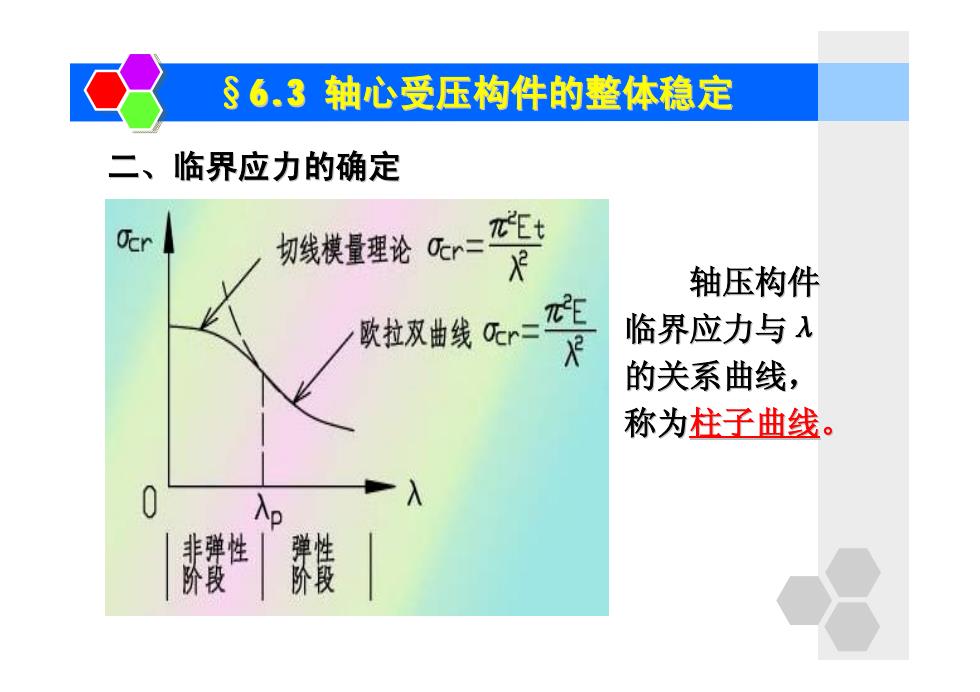
二、临界应力的确定 §6.3 轴心受压构件的整体稳定 轴压构件 临界应力与λ 的关系曲线, 称为柱子曲线
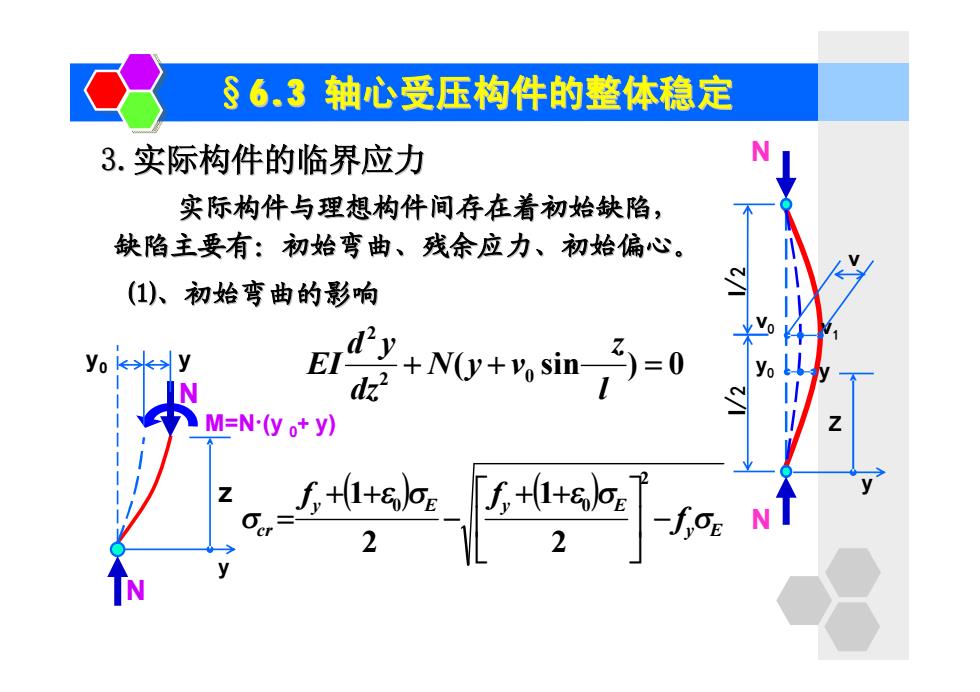
§6.3轴心受压构件的整体稳定 3.实际构件的临界应力 实际构件与理想构件间存在着初始缺陷, 缺陷主要有:初始弯曲、残余应力、初始偏心。 (1)、初始弯曲的影响 EI M=N-(y o+y)
3.实际构件的临界应力 实际构件与理想构件间存在着初始缺陷, 缺陷主要有:初始弯曲、残余应力、初始偏心。 ⑴、初始弯曲的影响 ( 0 sin ) 0 2 2 + + = l z N y v dz d y EI π §6.3 轴心受压构件的整体稳定 N N l/ 2 l/ 2 v0 y0 v1 y Z y v y0 y N N M=N·(y 0+ y) z y ( ) ( ) y E y E y E cr f f f s e s e s s ú - û ù ê ë é + + - + + = 2 0 0 2 1 2 1