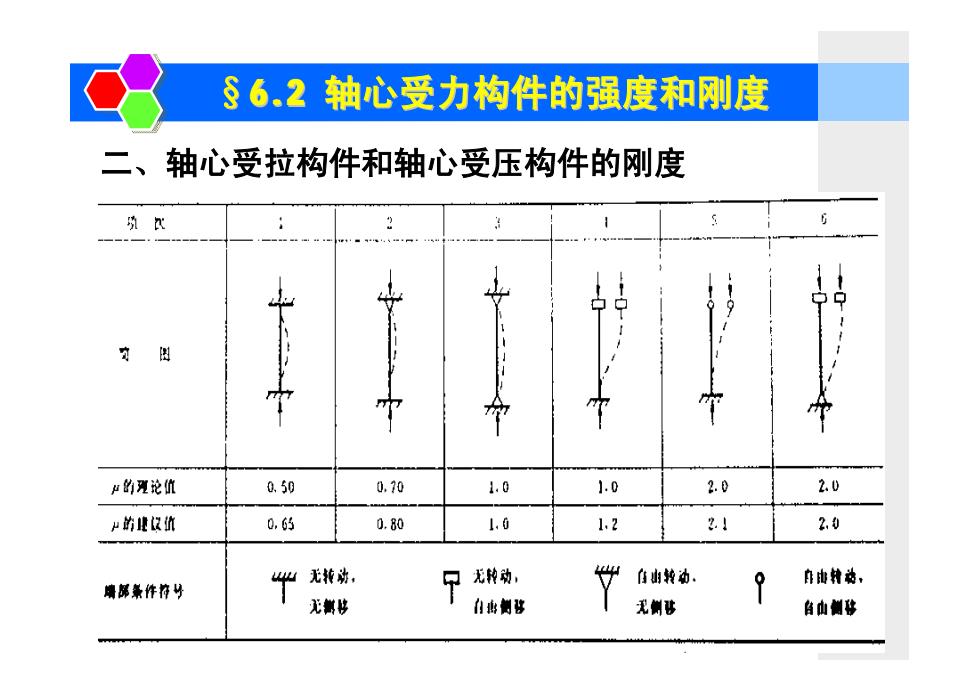
§6.2轴心受力构件的强度和刚度 二、轴心受拉构件和轴心受压构件的刚度 μ的理论值 0,50 0.70 1.0 1.0 2.0 2.0 少的业仅值 0,6的 0.80 1,0 1,2 21 2,0 山无兼动。 1无种动, 世 伯的转动, 年由转热, 端部条件符号 无制移 有郸侧移 孔侧移 自由前移
§6.2 轴心受力构件的强度和刚度 二、轴心受拉构件和轴心受压构件的刚度

§6,3轴心受压构件的整体稳定 稳定问题的概述 所谓的稳定是指结构或构件受载变形后,所处平衡状 态的属性。结构或构件失稳实际上为从稳定平衡状态经过 临界平衡状态,进入不稳定状态。临界状态的荷载即为结 构或构件的稳定极限荷载如:W。,,构件必须工作在临界荷载 之前。 稳定问题为钢结构的重点问题,所有钢结构构件均存 在稳定问题,稳定问题分构件的整体稳定和局部稳定。 一、整体失稳: 1.定义一当截面应力达到临界应力时,压杆不能维持直线平 衡,而发生弯曲,并维持曲线平衡的状态
§6.3 轴心受压构件的整体稳定 一、整体失稳: 1.定义—当截面应力达到临界应力时,压杆不能维持直线平 衡,而发生弯曲,并维持曲线平衡的状态。 稳定问题的概述 所谓的稳定是指结构或构件受载变形后,所处平衡状 态的属性。结构或构件失稳实际上为从稳定平衡状态经过 临界平衡状态,进入不稳定状态。临界状态的荷载即为结 构或构件的稳定极限荷载如:Ncr ,构件必须工作在临界荷载 之前。 稳定问题为钢结构的重点问题,所有钢结构构件均存 在稳定问题,稳定问题分构件的整体稳定和局部稳定

§6.3轴心受压构件的整体稳定 2.失稳形式 弯曲失稳一只有弯曲变形; 扭转失稳一只有扭转变形; 弯扭失稳一弯曲变形的同时伴随有扭转变形。 单对称截面绕对称轴(或不对称截面)弯曲失稳时, 由于截面的形心(内力作用点)与剪心(截面的扭转中心) 不重合,截面内的内力分量相对于剪心产生偏心产生扭 矩,从而产生扭转变形,故表现为弯扭失稳。 类似于工字型截面的双轴对称截面,弯曲稳定承载力 大于扭转失稳承载力,主要表现为弯曲失稳;其中极点对 称的截面(十字形截面)常发生扭转失稳
2.失稳形式 弯曲失稳-只有弯曲变形; 扭转失稳-只有扭转变形; 弯扭失稳-弯曲变形的同时伴随有扭转变形。 单对称截面绕对称轴(或不对称截面)弯曲失稳时, 由于截面的形心(内力作用点)与剪心(截面的扭转中心) 不重合,截面内的内力分量相对于剪心产生偏心产生扭 矩,从而产生扭转变形,故表现为弯扭失稳。 类似于工字型截面的双轴对称截面,弯曲稳定承载力 大于扭转失稳承载力,主要表现为弯曲失稳;其中极点对 称的截面(十字形截面)常发生扭转失稳。 第四章 轴心受力构件 §6.3 轴心受压构件的整体稳定
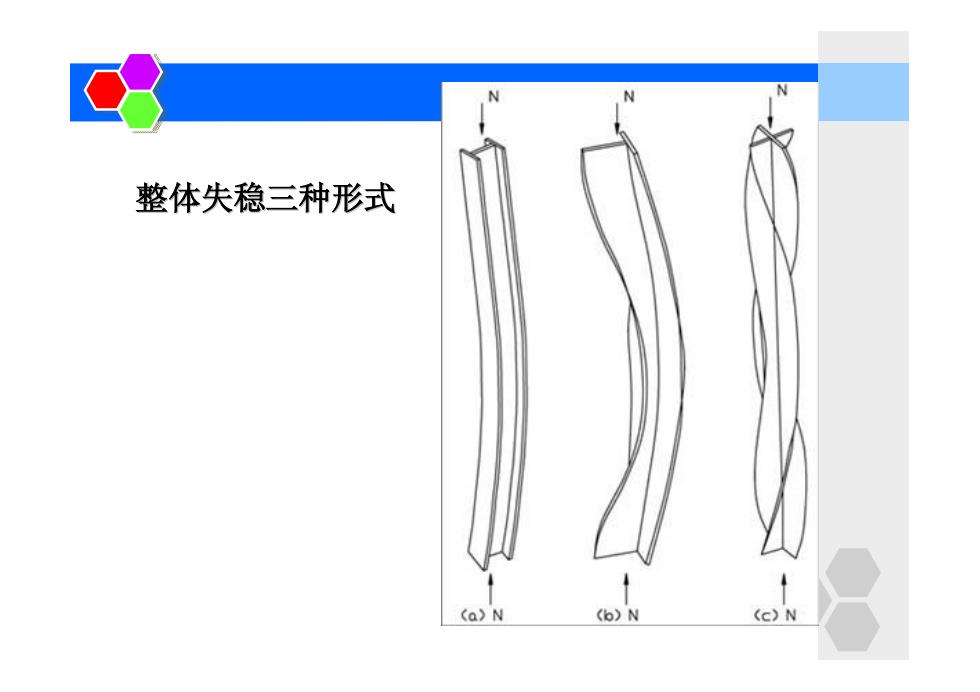
N 整体失稳三种形式 (a>N (b)N (c)N
整体失稳三种形式 第四章 轴心受力构件

§6.3轴心受压构件的整体稳定 3.整体稳定的计算方法 《规范》规定: A YR 即:N ≤f A 可见稳定计算关键是求p,亦即求O
《规范》规定: N f j A £ cr y f j = s f f A f N R y y cr R cr j g s g s s = £ = = 3.整体稳定的计算方法 即: j 可见稳定计算关键是求 ,亦即求 scr 第四章 轴心受力构件 §6.3 轴心受压构件的整体稳定