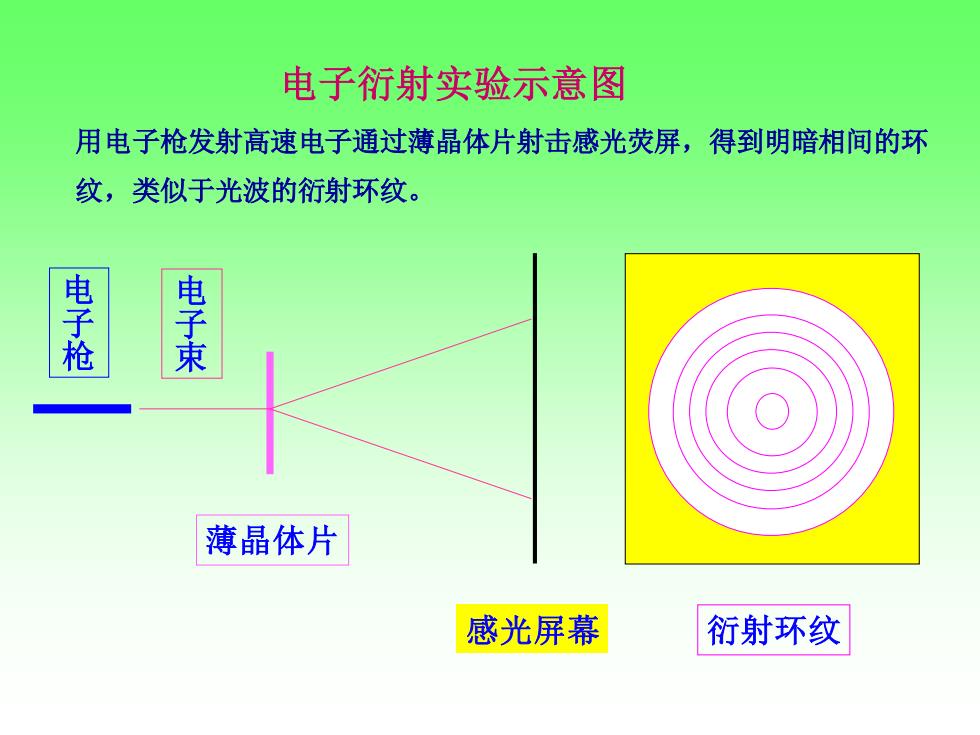
电子衍射实验示意图 用电子枪发射高速电子通过薄晶体片射击感光荧屏,得到明暗相间的环 纹,类似于光波的衍射环纹。 电子枪 电子束 薄晶体片 感光屏幕 衍射环纹
电子衍射实验示意图 用电子枪发射高速电子通过薄晶体片射击感光荧屏,得到明暗相间的环 纹,类似于光波的衍射环纹。 感光屏幕 薄晶体片 衍射环纹 电 子 枪 电 子 束

这种具有波粒二象性的微观粒子,其运动状态和宏观物 体的运动状态不同。例如,导弹、人造卫星等的运动,它 在任何瞬间,人们都能根据经典力学理论,准确地同时测 定它的位置和动量;也能精确地预测出它的运行轨道。但 是像电子这类微观粒子的运动,由于兼具有波动性,人们 在任何瞬间都不能准确地同时测定电子的位置和动量;它 也没有确定的运动轨道。所以在研究原子核外电子的运动 状态时,必须完全摒弃经典力学理论,而代之以描述微观 粒子运动的量子力学理论
这种具有波粒二象性的微观粒子,其运动状态和宏观物 体的运动状态不同。例如,导弹、人造卫星等的运动,它 在任何瞬间,人们都能根据经典力学理论,准确地同时测 定它的位置和动量;也能精确地预测出它的运行轨道。但 是像电子这类微观粒子的运动,由于兼具有波动性,人们 在任何瞬间都不能准确地同时测定电子的位置和动量;它 也没有确定的运动轨道。所以在研究原子核外电子的运动 状态时,必须完全摒弃经典力学理论,而代之以描述微观 粒子运动的量子力学理论

三、波函数和原子轨道 1926年奥地利物理学家薛定谔(E.Schrodinger)把电子运动帮光的 波动性理论联系起来,提出了描述核外电子运动状态的数学方程,称 为薛定谔方程。薛定谔方程把作为粒子物质特征的电子质量)、位能 ()和系统的总能量(E)与其运动状态的波函数0列在一个数学方程式中, 即体现了波动性和粒子性的结合。解薛定谔方程的目的就是求出波函 数以及与其相对应的能量E,这样就可了解电子运动的状态和能量的 高低。求得(x,y,z)的具体函数形式,即为方程的解。它是一个包含三 个常数项n、m和三个变量x、y、z的函数式。 返回
三、 波函数和原子轨道 1926年奥地利物理学家薛定谔(E.Schrödinger)把电子运动帮光的 波动性理论联系起来,提出了描述核外电子运动状态的数学方程,称 为薛定谔方程。薛定谔方程把作为粒子物质特征的电子质量(m)、位能 (V)和系统的总能量(E)与其运动状态的波函数()列在一个数学方程式中, 即体现了波动性和粒子性的结合。解薛定谔方程的目的就是求出波函 数以及与其相对应的能量E,这样就可了解电子运动的状态和能量的 高低。求得(x,y,z)的具体函数形式,即为方程的解。它是一个包含三 个常数项n、l、m和三个变量x、y、z的函数式。 返回

奥地利物理学家E.Schrodinger
奥地利物理学家E.Schrödinger

从理论上讲,通过解薛定谔方程可得出波函数,但薛定谔方程 的许多解在数学上是合理的,且运算极为复杂,只有满足特定条件 的解才有物理意义,用来描述核外电子运动状态。为了得到描述电 子运动状态的合理解,必须对三个参数n、I、m按一定的规律取值。 这三个函数,分别称为主量子数、角量子数和磁量子数。 求解方程得出的不是一个具体数值,而是用空间坐标(xy,z)来描述 波函数的数学函数式,一个波函数就表示原子核外电子的一种运动 状态并对应一定的能量值,所以波函数也称原子轨道。但这里所说 的原子轨道和宏观物体固定轨道的含义不同,它只是反映了核外电 子运动状态表现出的波动性和统计性规律。 为了方便,解方程时一般先将空间坐标(xy,z)转换成球坐 标吼r,8,),而后把,0,)分解为用表示的径向分布函 数R()和仅包含角度变量和的角度分布函数Y(O,)。为电子 与原子核间的距离,和代表角度。由于Ψ的角度分布与主量 子数无关,且相同时,其角度分布图总是一样的。在下章讨论 成键问题时,角度分布图有直接应用,故比较重要。图31为某 些原子轨道的角度分布图,图中的“+”、“”号表示波函数的 正、负值
从理论上讲,通过解薛定谔方程可得出波函数,但薛定谔方程 的许多解在数学上是合理的,且运算极为复杂,只有满足特定条件 的解才有物理意义,用来描述核外电子运动状态。为了得到描述电 子运动状态的合理解,必须对三个参数n、l、m按一定的规律取值。 这三个函数,分别称为主量子数、角量子数和磁量子数。 求解方程得出的不是一个具体数值,而是用空间坐标(x,y,z)来描述 波函数的数学函数式,一个波函数就表示原子核外电子的一种运动 状态并对应一定的能量值,所以波函数也称原子轨道。但这里所说 的原子轨道和宏观物体固定轨道的含义不同,它只是反映了核外电 子运动状态表现出的波动性和统计性规律。 为了方便,解方程时一般先将空间坐标 (x,y,z)转换成球坐 标(r,, ),而后把(r,, )分解为用r表示的径向分布函 数R(r)和仅包含角度变量和的角度分布函数Y (,)。r为电子 与原子核间的距离,和代表角度。由于的角度分布与主量 子数l无关,且l相同时,其角度分布图总是一样的。在下章讨论 成键问题时,角度分布图有直接应用,故比较重要。图3-1为某 些原子轨道的角度分布图,图中的“+”、“-”号表示波函数的 正、负值