
Landau理论的具体表达: 自由能作于为序参量的函数。 序参量:标量、矢量、张量或复数。 在相变点附近,将自由能展开: F(T,)=F(T)+a2(T)n2+&,(T)m+.… 2023/6/28 17
2023/6/28 17 Landau理论的具体表达: 自由能作于为序参量的函数。 序参量:标量、矢量、张量或复数。 在相变点附近,将自由能展开: 2 4 0 2 4 F T F T T T ( , ) ( ) ( ) ( ) = + + +
Ferroelectric Bi3.25La0.75TigO12 125.0nm YSZ (100j 19.5° SrRuo, 62.5nm (1101 0.0nm 2023/6/28 18
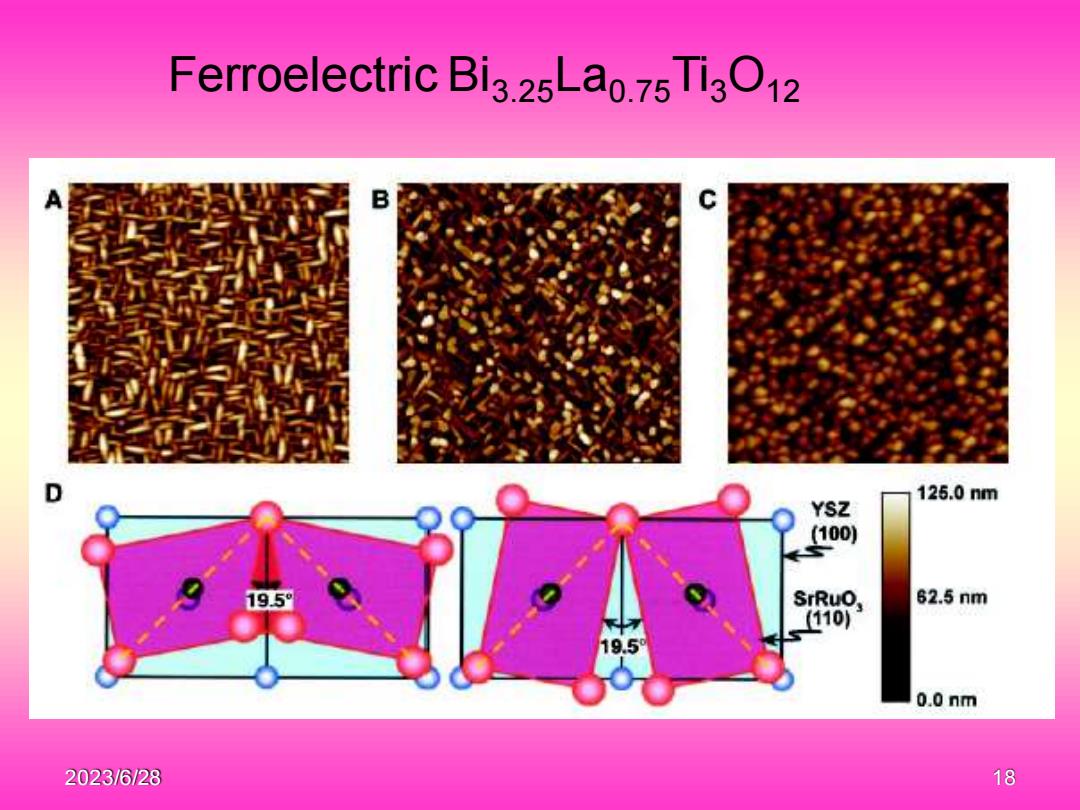
2023/6/28 18 Ferroelectric Bi3.25La0.75Ti3O12

F(T,7)=E(T)+C2(T)n+C(T)n+.. T'>T。 7=0使自由能达到极小C2(T')>0 TW<T 7≠0使自由能达到极小 a2(T"m<0 a2(T')-→a2(T") 连续变化要求( 2(Tc)=0 a2 (T)=ao(T-T) 0>0 2023/6/28 19
2023/6/28 19 T Tc = 0 使自由能达到极小 2 (T) 0 T" Tc 0 使自由能达到极小 2 (T") 0 ( ) ( ) 2 T → 2 T 连续变化要求, 2 (Tc ) = 0 ( ) ( ) 2 T 0 T −Tc = • 0 0 2 4 0 2 4 F T F T T T ( , ) ( ) ( ) ( ) = + + +