
推论对任意x∈R且x与e,不共线,则初等反射阵H=I,-2aT使得。 血共中高=业, 初等反射阵的应用主要基于上述的定理和推论。推论的结果称为用 ousehol der查换化x与e,月方向(共线)。 This documentis prduced byriaversion ofPrnh Visit www.prinashcfor more informion
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

例试用Householder变换化向量x=(-3.0,0,4)T与e,同方向。+ 屏法1.取x=xL=5,则M= x-5e1= ke-5ao-80.0.4, /-3004 H=1-2m=10500 50 050 使x=5e1 4003 法2取a=l=-5,则w+g, x+5g1 (2,0,0,4, f300-4 H=I-2uu= 0500 0050 使=-5g1 -400-3 This documentis produced bytril versin ofPrVisit www.prinashcmfor more infomtion
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

4.2.2 Givens矩阵 在R2中,向量x=(⑤,)依顺时针方向旋转角度6变为y=(,”2),则x与y,的 长度相等,且其坐标满足.-cos9血9丫台) 2-m6cosa人5 称T-c6,2)为平面旋转特胖,它是一个正交矩阵,准广到R上,即得 -smcose This documentis prduced byria version ofPrnhVisit www.prinashcfor more informion
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information
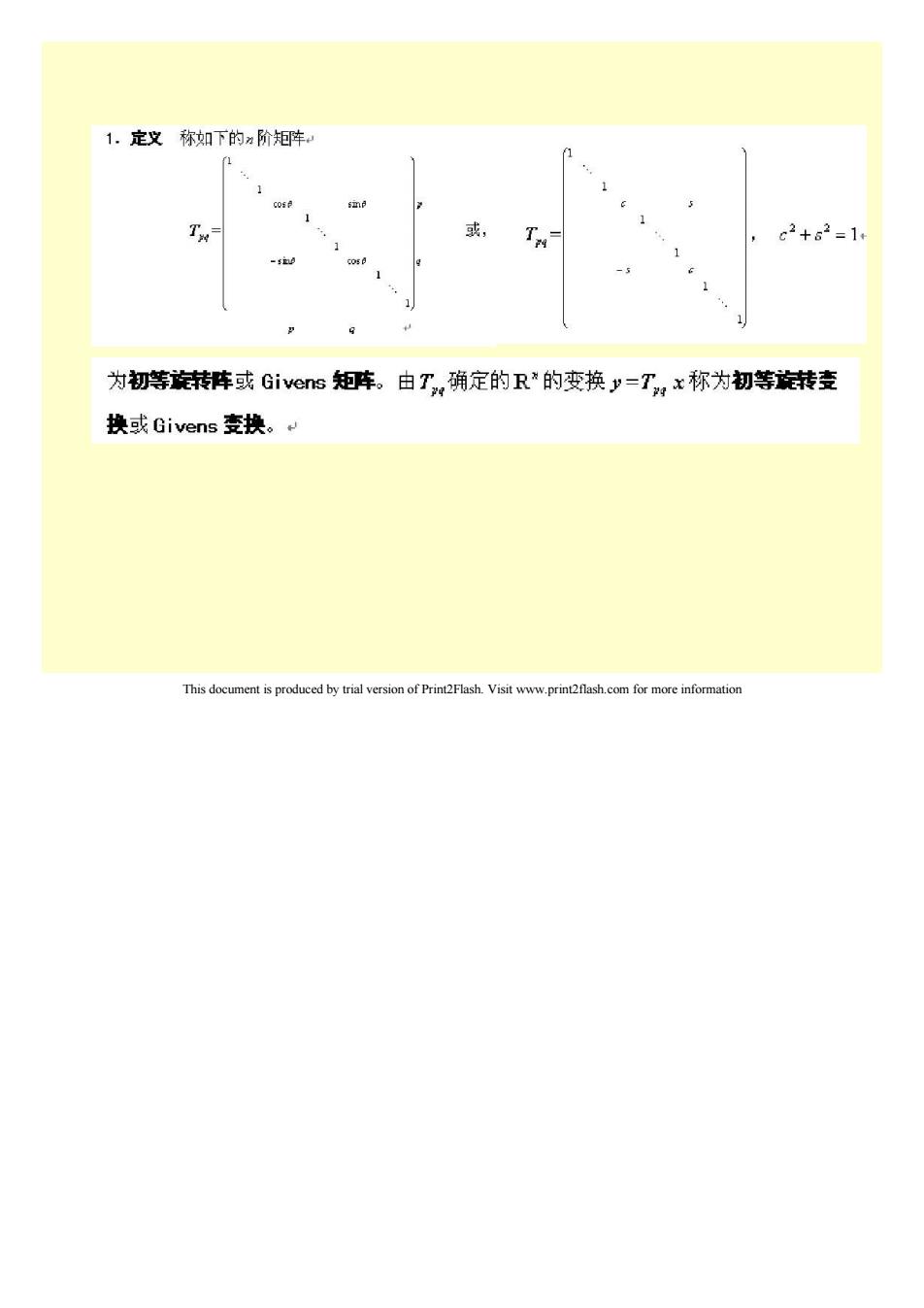
1.定义称如下的m阶矩阵 c2+62=1 为初等转车或Givens知车。由T,确定的R”的变换y-T,x称为初等转麦 换或Givens变换。 This documentis produced bytril versinofPrVisit www.prinashcmformore infomio
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

性质1了,是正交阵且tTm=1。” 性质2设x=(6.6,…,5)FeR,则存在初等旋转阵Tg,使了,x的第 个分量非负,第g个分量为0,而其余分量不变。 证了4x 可见除P,g分量外其余分量不变 9 若=,0,取c=1s=0,则T,=1,且Tgx满足所述条件; 若号+号+0,取= 店牙房安则7的第个分量为 c+安份+分-得+安≥0 1 而TNx的第g个分呈 -85,+c5,0 证毕, This documentis produced byria version ofPrnh Visit www.prinashcmfor more informtion
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information