
子),值得特别提一提。它的所有观测到的谱线的频率都遵从 巴耳末经验公式: -R(停-》 其中”和m是正整数(m>n),而R是一个表征氢原子的常 数(里德伯常数). 更复杂的原子不存在这样的简单公式,不过各个频率之 间总有-一定的联系:属于同一光谱的两个频率,它们之和或 它们之差的频率也必定出现在这同一光谱中.说得更确切些 我们可以就每一种原子建立一个数值表,即光谱项表,让光谱 中的任何一个频率都等于这个表中两项数值之差。这个法则 称为盟德伯-里兹组合原则(1905),巴耳未公式只是它的一个 特例.反过来,两个光谱项之差却未必都是光谱中的一个频 率。我们可以定出几条并不太难的选择定则,根据它们去判 断哪些光谱项之差能在光谱中出现,而哪些则不能 这些实验享实与经典的卢瑟福原子辐射理论明显不符, 的确,如果我们不只限于考虑库仑相互作用,而是严格按照洛 伦兹电子论把原子内电子与电磁场的相互作用考虑进来,那 么卢瑟福模型本身就会遇到严重矛盾。电子沿它们的轨道运 动时会发出辐射而不断失去能量,最终应该沿螺旋线掉人核 内。在每一时刻,我们在发射辐射中观测到的频率,应该等于 轨道运动的频率或者它的一个谐波频率,这个频率将随着轨 道运动的减慢而逐渐变化,因而观测到的本应该是一个连续 的发射光谱。所以,经典的卢瑟福原子理论既不能说明原子 的稳定性,也不能说明线光谱的存在。在物质与光的相互作 用中我们遇到了不连续性的一种新的表现形式,而经典理论 在这种场合下预言的却是连续变化 ·20

9.原子能级的量子化 1913年,玻尔用一个同经典概念不相容的新假定来完善 光的量子假说,终于以一种普遍的方式解释了光谱;这个新假 定就是原子能级的量子化, 按照玻尔的理论,原子并不象一个能以连续方式交换能 量的经典系统,它只能存在于某些稳定态即量子态,每一个量 子态都有完全确定的能量,这就是说,原子的能量是量子化 的。原子的能量只能跳跃式变化,每一次跳跃相应于原子从 一个态跃迁到另一个态。 这个假设使我们能用量子来详细说明光的发射和吸收机 制。只要总能量是守恒的,在有光照射时,一个能量为E;的 原子有可能吸收一个光子h如而跃迁到一个能量较高的E; (>E)的状态,即有 hy=Ei-Ei 同样,原子也可能发射一个光子m而跃迁到一个能量较低 E(<E)的状态,这个光子的频率满足关系式 hy=E:一Ek. 若原子本来已处于最低能态(基态),它就不可能辐射而保持 稳态。 关于每一种原子都有自己的特征谱线而且它们满足里德 伯-里兹组合原则的问题,可以按如下方式来解释:若不计及 因子h,各个光谱项就等于原子的各个盘子态的能量。具体 到氢原子的情形,假定各能级的能量由公式 En=-h(m-1,2,3,…,00) (1.7) 给出,那么立即就能推得巴耳末公式。 原子能级量子化的另一个证据,是夫兰克-赫兹就电子与 ·21

原子间的非弹性碰撞所做的实验提供的(1914).这个实验用 单一能量的电子去轰击原子而测量散射电子的动能。·这样, 借助减法便能推知原子在碰撞中吸收的能量.令E,E:, E,··为原子的一系列量子化能级,T为人射电子的动能.在 实验条件下,靶中的原子实际上全都处于它们的基态.如果 T小于第一激发态能量与基态能量之差(E.一E),原子则不 可能吸收能量,这时所有的碰撞都是弹性碰撞.然而,如果 T>E,一E,则会发生非弹性碰撞,电子在碰撞中将失去等 于E,一E。的能盘,而原子进人它的第一激发态。这一点 同实验观测结果完全一致。同样,我们还能观测到在T> E,一E,时出现第二激发态的激发,等等. 因此,原子能级的量子化已被视为是实验事实。这个性 质并非是原子独有的。随着实验工作的进展,特别是光谱学 领域取得的实验成果表明,在分子乃至更复杂的粒子系统中 也存在着量子化现象。由此可见,我们面对的是一种无法用 经典微粒说加以解释的非常普遍的物质性质。 10.其它量子化的例子空间量子化 实验上观测到的另一种量子化是原子系统的取向量子化 或者说“空间量子化”。我们发现,只要把原子置于外磁场中, 每一次它都会有一个占优势的取向.原子系统的这种取向并 不是任意的,而只能取一些分立的数值。 顺磁原子束(或分子束)在非均匀磁场中发生偏转的斯特 恩-革拉赫实验(1922)为这种空间量子化提供了最直接的证 据。按照有关假说,顺磁原子具有一个永磁矩“,而且可以看 作是其角动量I正比于“的一个小的元回转器: μ=ML. 和l的取向就决定了原子本身的取向,在磁场H中,这 ●22◆
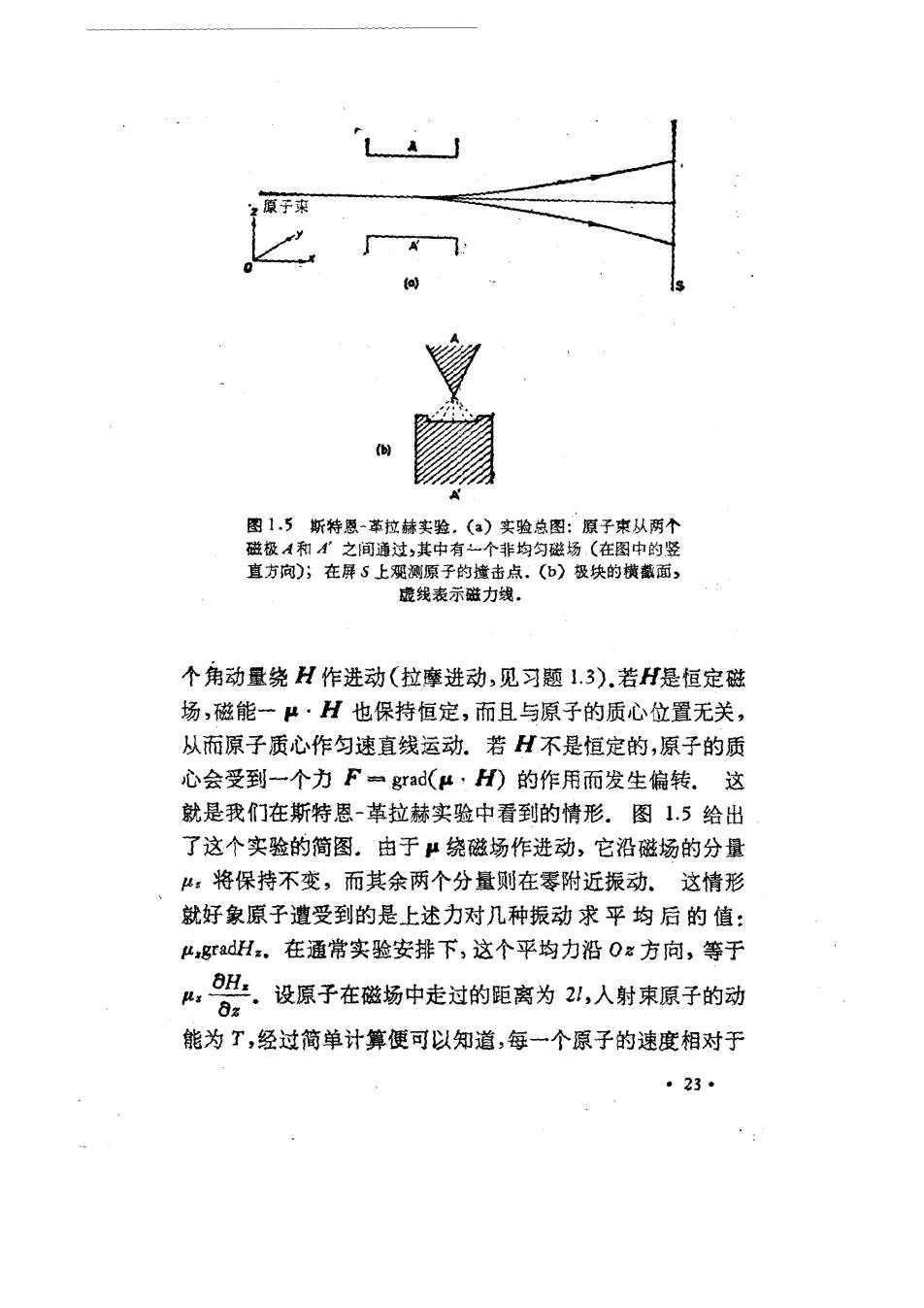
图1.5斯特恩-茶拉赫实验.()实验总图:原子来从两个 磁极A和”之间通过,其中有个非均匀磁场(在图中的竖 直方向);在屏5上观测原子的撞击点。()极块的面, 线表示磁力 个角动量绕H作进动(拉摩进动,见习题13).若H是恒定磁 场,磁能一μ·H也保持恒定,而且与原子的质心位置无关, 从而原子质心作匀速直线运动。若H不是恒定的,原子的质 心会受到一个力F=grad(μ·)的作用而发生偏转.这 就是我们在斯特恩-革拉赫实验中看到的情形.图1.5给出 了这个实验的简图.由于“绕磁场作进动,它沿磁场的分量 “:将保持不变,而其余两个分量则在零附近振动、这情形 就好象原子遭受到的是上述力对几种振动求平均后的值: 4 gradH,在通常实验安排下,这个平均力沿0x方向,等于 一船。设原子在磁杨中走过的距离为2,人射束眼子的动 能为T,经过简单计算便可以知道,每一个原子的速度相对于 ·23·

它的初始方向0:偏转了-个角度心4()(份〉由此 可见,偏转角正比于:在磁场方向的分量。如果束中原子作 无规则取向,4:将取从一:到+“之间的一切值,因而偏转角 也应取两个相应极值之间的一切值。这样,原子撞击在屏上 应该形成的是一个沿O:方向伸长的大斑块.然而,人们实 际观测到的却是沿0z方向等间距排列的一系列小斑点。如 果改变磁场(从而改变H/8z),这些小斑点之间的间隔距离 随之变化,但斑点的分布花样及其他一切均无变化,特别是小 斑点的数目无保持不变.每一个小斑点对应于4:的一个确 定值.结果,4,是一个取1个不同值的量子化的量.角动量 的分量1:显然也有同样的性质。 人们也许可以对斯特恩-革拉赫实验的这种解释提出非 难,因为它是建立在关于原子顺磁性起源的一个非常特别的 假说之上,即认为存在一种正比于角动量的永磁矩.我们这 里不打算详细阐述支持这个假说的那些事实和论证(迴转磁 效应,郎之万顺磁磁化率理论,等等),因为后来量子力学的发 展已完全证实了这个假说.、即使怀疑上述解释细节的人,他 倘若不假定有一些表征内部运动的量是被量子化的,也一定 难以解释屏上存在着2个明显分开的小斑点的事实。事实 上,就原子质心运动遵从经典力学运动规律而言,质心的运动 轨迹是由磁铁人口处原子的动力学状态完全确定了的.屏上 出现多少伸展开来的撞击点分布表明,原子并非全都处在相 同的初始条件下,确定初态的那些动力学变量是按统计规律 分布在一个多少扩散开来的数域上.存在着飞个明显分开的 小斑点这一事实告诉我们,这种统计分布至少是不连续的,换 句话说,原子中有一些动力学变量是量子化的。由于原子实 际上全都处于它们的基态(否则它们将辐射),这里我们遇到 ,24·