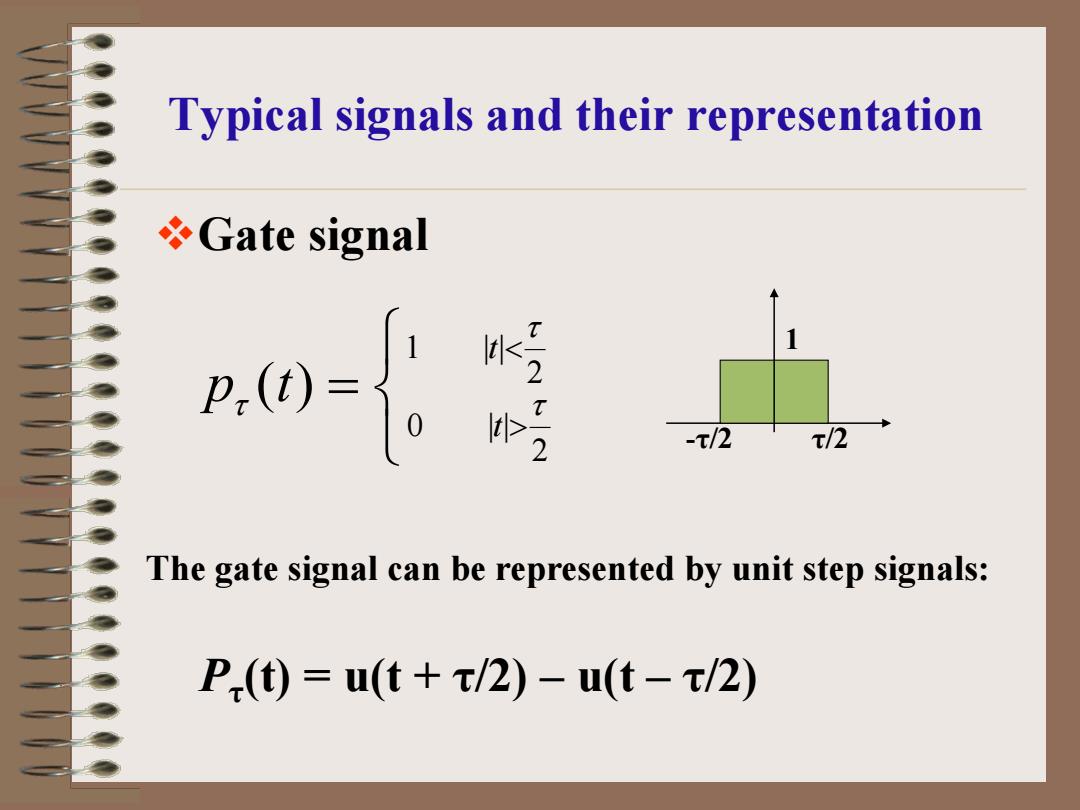
Typical signals and their representation Gate signal t -t/2 /2 The gate signal can be represented by unit step signals: P()=u(t+t/2)-u(t-/2)
Typical signals and their representation Gate signal = < > 2 1 | | 2 0 | | ( ) τ τ τ t t p t The gate signal can be represented by unit step signals: Pτ(t) = u(t + τ/2) – u(t – τ/2) -τ/2 τ/2 1

Typical signals and their representation Unit Impulse Signal [8(t)dt =1 δ(t)=0 t≠ 5(t)is non-zero only at t=0,otherwise is 0 5(t)could not be represented by a constant even at t=0, but by an integral. Regular function has exact value at exact time. Obviously,6(t)is not a Regular function,but Singularity function (or Generalized function)
Typical signals and their representation Unit Impulse Signal ( ) 0 0 ( ) 1 = ≠ = ∫ ∞ −∞ t t t dt δ δ • δ(t) is non-zero only at t=0,otherwise is 0 • δ(t) could not be represented by a constant even at t=0, but by an integral. • Regular function has exact value at exact time. Obviously,δ(t) is not a Regular function, but Singularity function(or Generalized function)
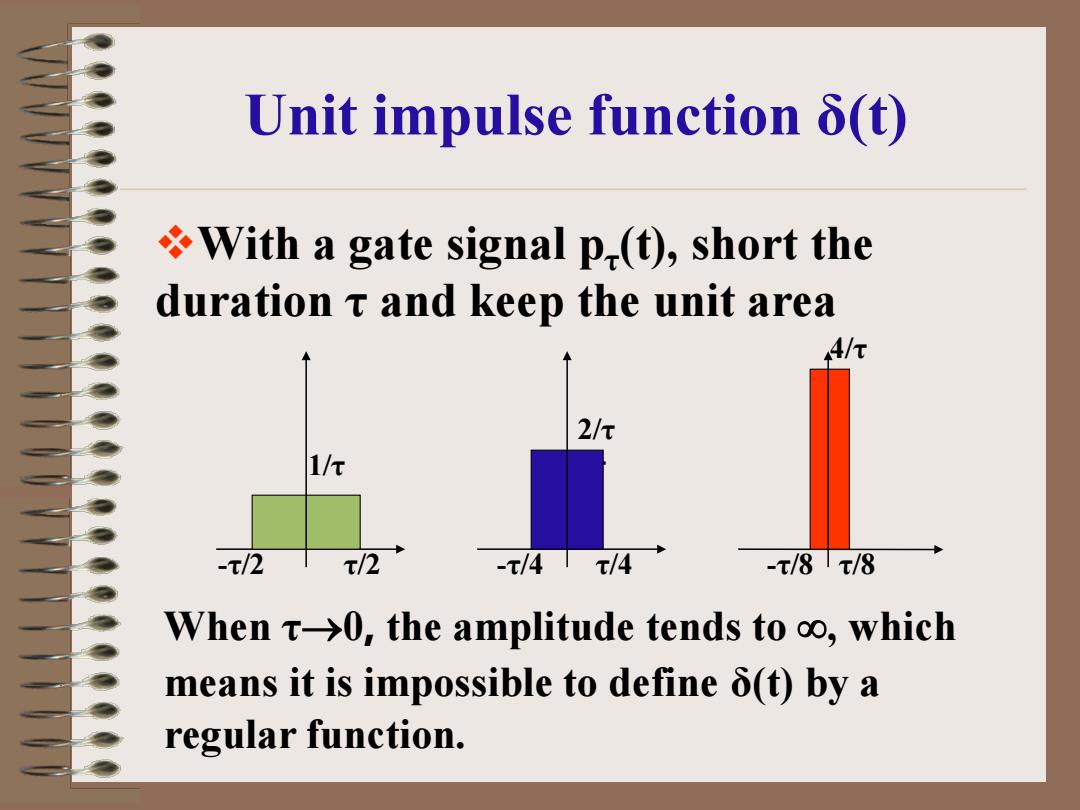
Unit impulse function 5(t) With a gate signal p,(t),short the duration t and keep the unit area 4/元 2/元 1/e -t/2 /2 -τ/4 τ/4 -τ/8T/8 When t->0,the amplitude tends to oo,which means it is impossible to define 6(t)by a regular function
Unit impulse function δ(t) With a gate signal pτ(t), short the duration τ and keep the unit area When τ→0, the amplitude tends to ∞, which means it is impossible to define δ(t) by a regular function. -τ/2 τ/2 1/τ -τ/4 1/τ τ/4 2/τ -τ/8 4/τ τ/8

Properties ofδ(t) Sampling Property ∫f(t)8(t)dt=fo) Briefly understanding: When t≠0,δ()=O,then f().δ(t)=0 .When t=0,f(t)=f(0)is a constant.Based on the definition ofδ(),it is easy to get: 0 ∫f06t)di=∫fo)8u)dh=f0)∫δ)dh=fo)
Properties of δ(t) Sampling Property ∫ ∞ −∞ f (t)δ (t)dt = f (0) Briefly understanding: •When t ≠ 0, δ(t)=0, then f(t)·δ(t)=0 •When t = 0, f(t) = f(0) is a constant. Based on the definition of δ(t), it is easy to get: ∫ ∫ ∫ ∞ −∞ ∞ −∞ ∞ −∞ f (t)δ (t)dt = f (0)δ (t)dt = f (0) δ (t)dt = f (0)

Properties ofδ(t) 必δ(t)shift δ() δ(t-t) 0 0 7 5(t)times a constant A: Aδ() A is called impulse intension which is the area of the integral
Properties of δ(t) δ(t) shift δ(t) 0 t δ(t-τ) 0 τ t δ(t) times a constant A: Aδ(t) A is called impulse intension which is the area of the integral