
Example 3 And therefore,by differentiating and using the chain rule, r=2r网+25(-例.y≥0
Example 3 ◼ And therefore, by differentiating and using the chain rule, 𝑓𝑌 = 1 2 𝑦 𝑓𝑋 𝑦 + 1 2 𝑦 𝑓𝑋 − 𝑦 , 𝑦 ≥ 0
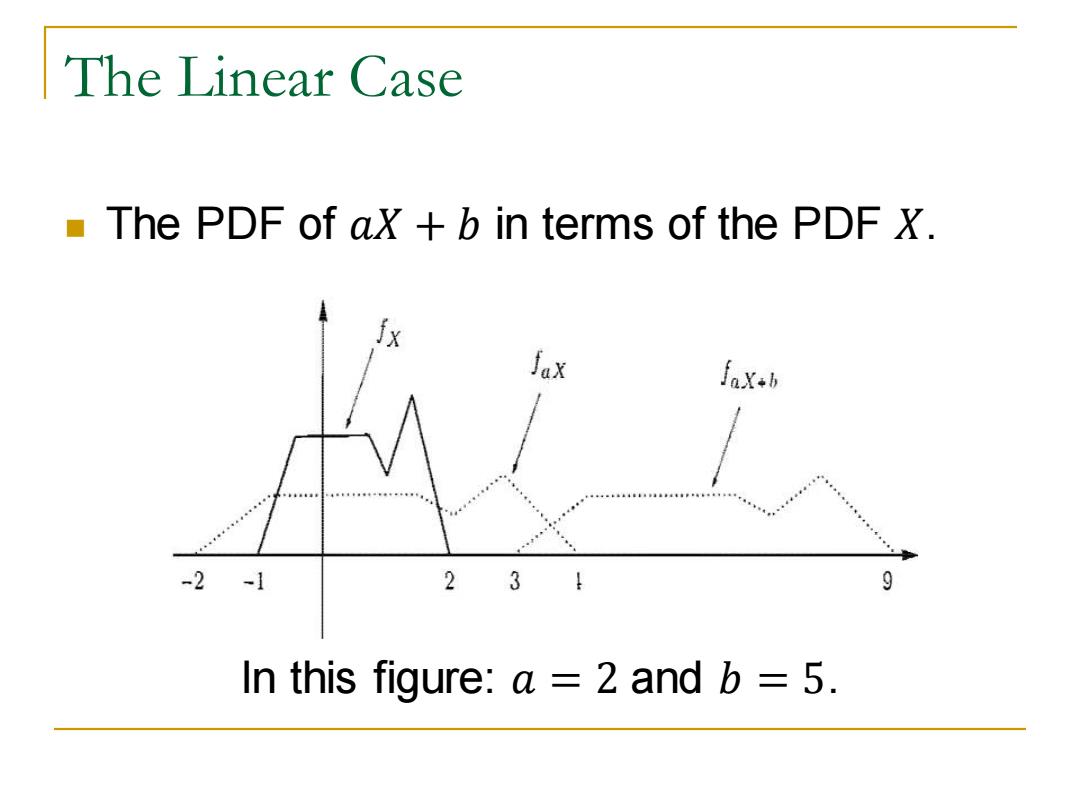
The Linear Case The PDF of ax +b in terms of the PDF X. -2 -1 23 9 In this figure:a =2 and b =5
The Linear Case ◼ The PDF of 𝑎𝑋 + 𝑏 in terms of the PDF 𝑋. In this figure: 𝑎 = 2 and 𝑏 = 5
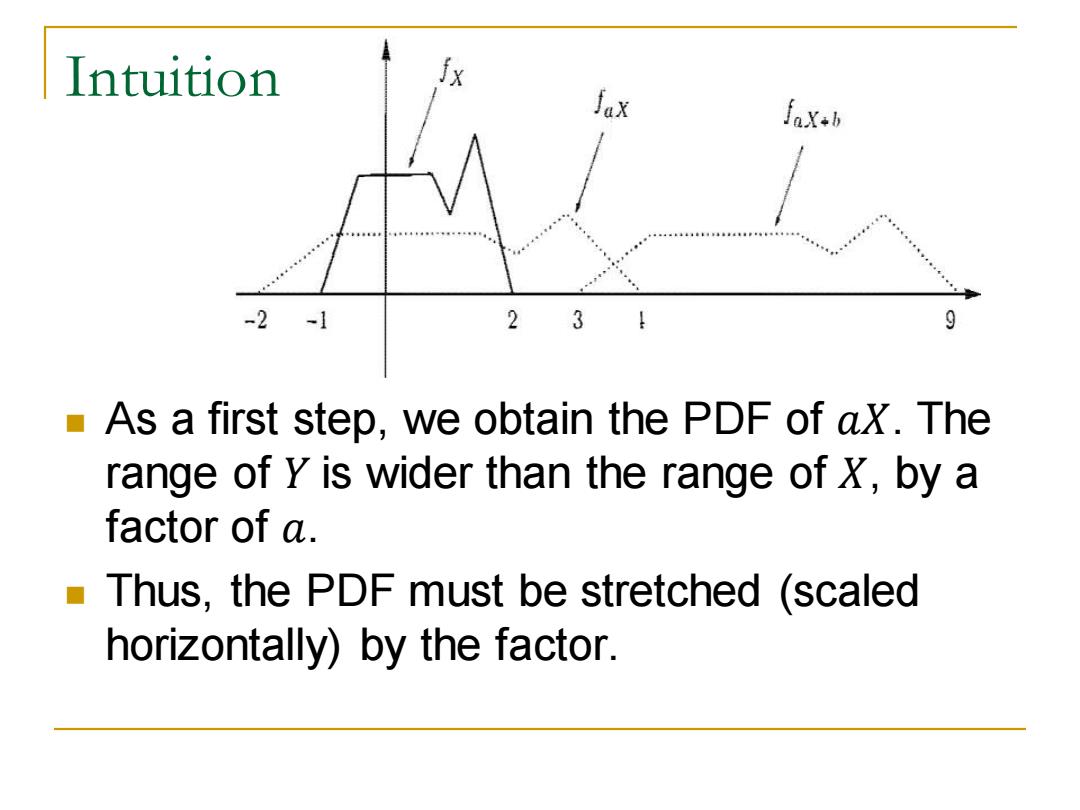
Intuition ix JaX fax-b -2-1 234 9 As a first step,we obtain the PDF of ax.The range of Y is wider than the range of X,by a factor of a. Thus,the PDF must be stretched (scaled horizontally)by the factor
◼ As a first step, we obtain the PDF of 𝑎𝑋. The range of 𝑌 is wider than the range of 𝑋, by a factor of 𝑎. ◼ Thus, the PDF must be stretched (scaled horizontally) by the factor. Intuition
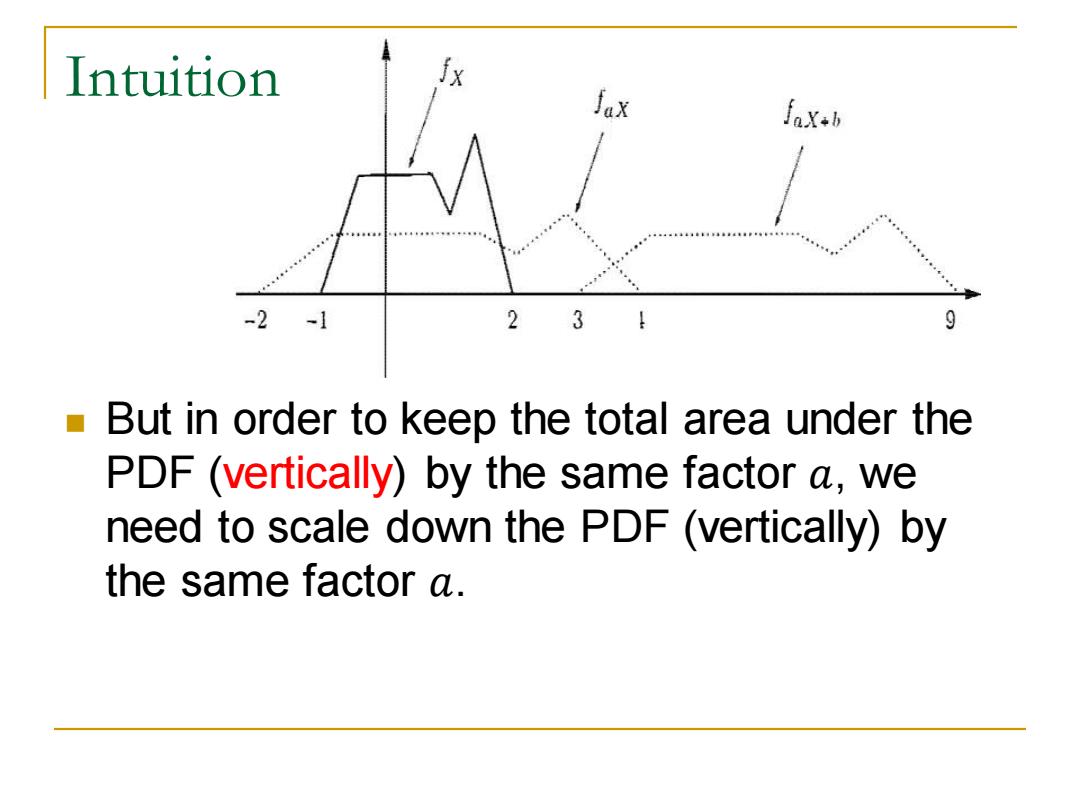
Intuition fx JaX fax-b -2-1 23 9 But in order to keep the total area under the PDF (vertically)by the same factor a,we need to scale down the PDF(vertically)by the same factor a
◼ But in order to keep the total area under the PDF (vertically) by the same factor 𝑎, we need to scale down the PDF (vertically) by the same factor 𝑎. Intuition
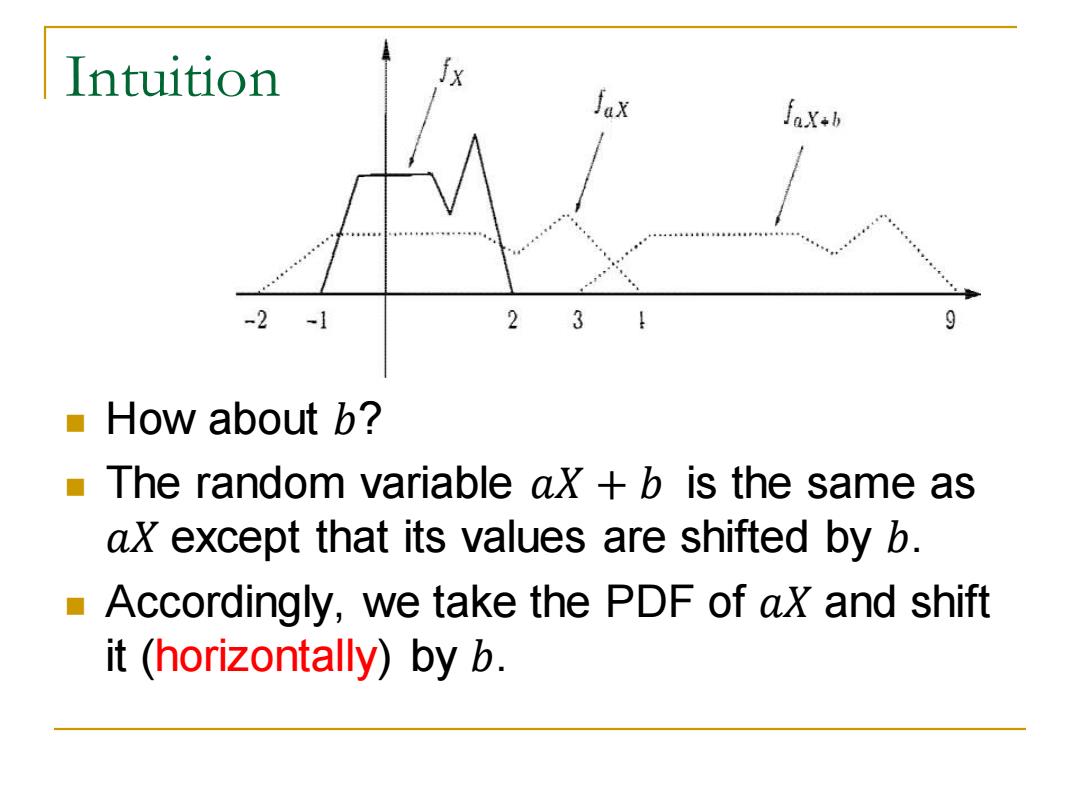
Intuition fx JaX fax-b -2-1 3 9 How about b? The random variable ax +b is the same as ax except that its values are shifted by b. Accordingly,we take the PDF of ax and shift it (horizontally)by b
◼ How about 𝑏? ◼ The random variable 𝑎𝑋 + 𝑏 is the same as 𝑎𝑋 except that its values are shifted by 𝑏. ◼ Accordingly, we take the PDF of 𝑎𝑋 and shift it (horizontally) by 𝑏. Intuition