
2.3热力学的一些基本概念 3.相平衡(phase equilibrium) 多相共存时,各相的组成和数量不随时 间而改变。 4.化学平衡(chemical equilibrium) 反应体系中各物的数量不再随时间而 改变。 2025/1112
2025/1/12 3.相平衡(phase equilibrium) 多相共存时,各相的组成和数量不随时 间而改变。 4.化学平衡(chemical equilibrium ) 反应体系中各物的数量不再随时间而 改变。 2.3 热力学的一些基本概念

2.3热力学的一些基本概念 四、状态函数 体系的一些性质,其数值仅取决于体系所 处的状态,而与体系的历史无关;它的变化值 仅取决于体系的始态和终态,而与变化的途径 无关。具有这种特性的物理量称为状态函数 (state function)。 状态函数的特性可描述为:异途同归,值 变相等;周而复始,数值还原。 状态函数在数学上具有全微分的性质。 2025/1/12
2025/1/12 体系的一些性质,其数值仅取决于体系所 处的状态,而与体系的历史无关;它的变化值 仅取决于体系的始态和终态,而与变化的途径 无关。具有这种特性的物理量称为状态函数 (state function)。 状态函数的特性可描述为:异途同归,值 变相等;周而复始,数值还原。 状态函数在数学上具有全微分的性质。 四、状态函数 2.3 热力学的一些基本概念

2.3热力学的一些基本概念 五、状态方程(state equation ) 体系状态函数之间的定量关系式称为状态方 程(state equation)。 对于一定量的单组分均匀体系,状态函数TP,V 之间有一定量的联系。经验证明,只有两个是独立 的,它们的函数关系可表示为: T=f (p,V) p=f (TV) V=f (p,T) 例如,理想气体的状态方程可表示为:pV=nRT 2025/1/12
2025/1/12 体系状态函数之间的定量关系式称为状态方 程(state equation )。 对于一定量的单组分均匀体系,状态函数T,p,V 之间有一定量的联系。经验证明,只有两个是独立 的,它们的函数关系可表示为: T=f(p,V) p=f(T,V) V=f(p,T) 例如,理想气体的状态方程可表示为:pV=nRT 五、状态方程(state equation ) 2.3 热力学的一些基本概念
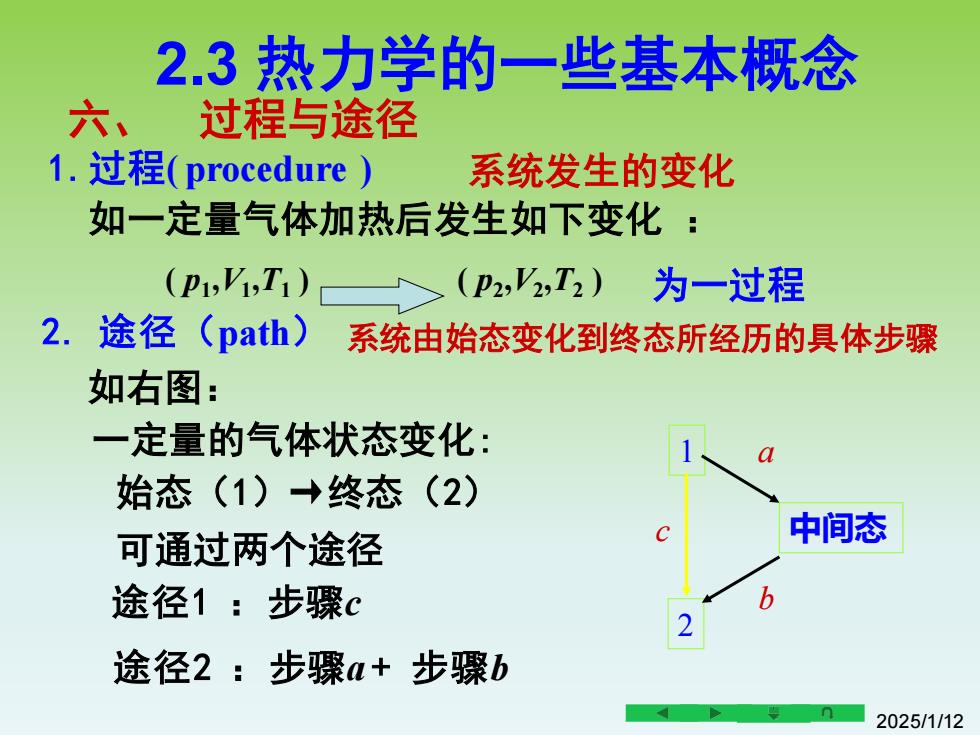
2.3热力学的一些基本概念 六、过程与途径 1.过程(procedure) 系统发生的变化 如一定量气体加热后发生如下变化: (P1,T1)(P2,T2)为一过程 2.途径(path) 系统由始态变化到终态所经历的具体步骤 如右图: 一定量的气体状态变化: 始态(1)→终态(2) 可通过两个途径 中间态 途径1:步骤c b 途径2:步骤a+步骤b 2025/1112
2025/1/12 六、 过程与途径 如一定量气体加热后发生如下变化 : ( p1 ,V1 ,T1 ) ( p2 ,V2 ,T2 ) 为一过程 2. 途径(path) 1.过程( procedure ) 系统发生的变化 系统由始态变化到终态所经历的具体步骤 如右图: 一定量的气体状态变化: 可通过两个途径 始态(1)→终态(2) 途径1 :步骤c 途径2 :步骤a + 步骤b 1 2 c 中间态 a b 2.3 热力学的一些基本概念

2.3热力学的一些基本概念 3.过程的分类 (1)恒温过程 即dT=0; 整个过程中,系统的温度保持恒定 等温过程:即△T=0; 始态温度(T1)=终态温度(T2)=环境温度(Tx) 即T1=T2=Tex, 2025/1/12
2025/1/12 3.过程的分类 (1)恒温过程 即 dT = 0; 整个过程中,系统的温度保持恒定 等温过程: 即 ΔT = 0; 始态温度(T1)= 终态温度(T2)= 环境温度(Tex) 即 T1=T2=Tex, 2.3 热力学的一些基本概念