
1概述 生产阻力取决于生产工艺过程的特点,有如下几种情 况: >生产阻力为常数,如车床; >生产阻力为机构位置的函数,如压力机; >生产阻力为执行构件速度的函数,如鼓风机、 搅拌 机等; >生产阻力为时间的函数,如球磨机、揉面机等; 本课程所讨论机械在外力作用下运动时,假定外力为已知。 所量大 KINJIANG UNIVERSITY 机械设计教研室 理械
机原 理械 生产阻力取决于生产工艺过程的特点,有如下几种情 况: ➢生产阻力为常数,如车床; ➢生产阻力为机构位置的函数,如压力机; ➢生产阻力为执行构件速度的函数,如鼓风机、搅拌 机等; ➢生产阻力为时间的函数,如球磨机、揉面机等; 本课程所讨论机械在外力作用下运动时,假定外力为已知
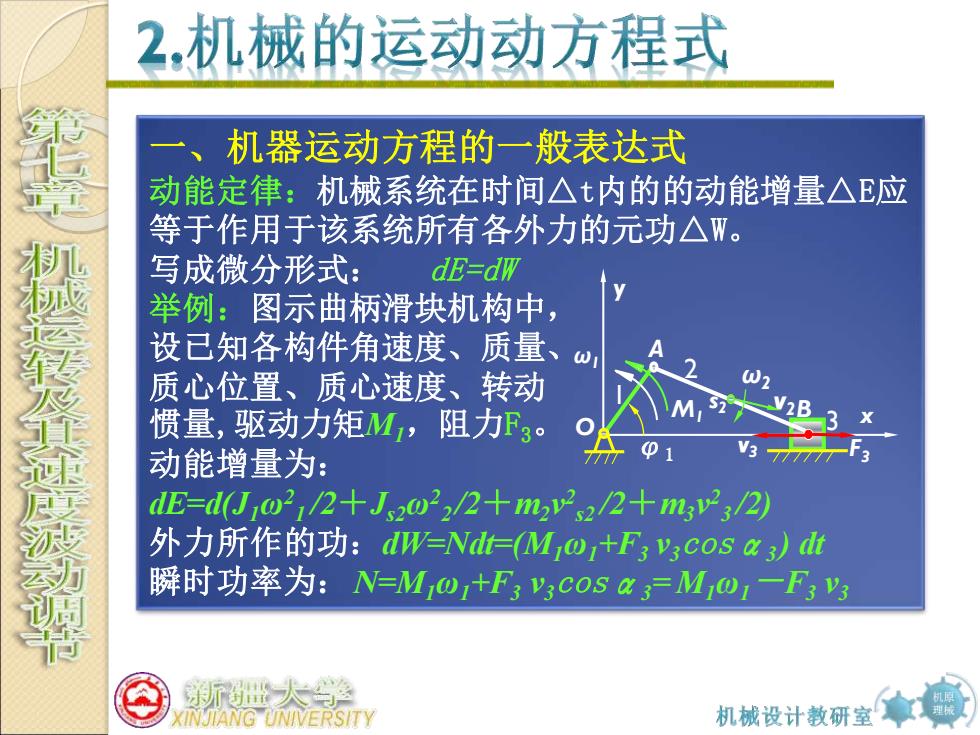
2,机械的运动动方程式 一、机器运动方程的一般表达式 动能定律:机械系统在时间△t内的的动能增量△E应 等于作用于该系统所有各外力的元功△W。 写成微分形式: dE=dW 举例:图示曲柄滑块机构中, 设已知各构件角速度、质量、 质心位置、质心速度、转动 惯量,驱动力矩M,阻力F3。 M V2B ● 动能增量为: 77 dE=d0o2/2十Jo2/2+m22/2+32 外力所作的功:dW-Ndt-(Mj@j+F,cosx 瞬时功率为:N=M+F3 v3cos a 3=M@1一F 世大学 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 一、机器运动方程的一般表达式 动能定律:机械系统在时间△t内的的动能增量△E应 等于作用于该系统所有各外力的元功△W。 写成微分形式: dE=dW 举例:图示曲柄滑块机构中, 设已知各构件角速度、质量、 质心位置、质心速度、转动 惯量,驱动力矩M1,阻力F3。 动能增量为: dE=d(J1ω2 1 /2+Js2ω2 2 /2+m2v 2 s2 /2+m3v 2 3 /2) 外力所作的功:dW=Ndt=(M1ω1+F3 v3cosα3 ) dt 瞬时功率为:N=M1ω1+F3 v3cosα3= M1ω1-F3 v3 x y 1 2 3 s2 O A B φ1 ω2 M1 ω1 v2 F3 v3

2,机械的运动动方程式 运动方程为: d0o22十J222十n22/2十m,/2=0M01F,y)dt 推广到一般,设有个活动构件,用E表示其动能。 则有: E=之E 二2(m心+2) 设作用在构件i上的外力为F,力矩M为,力F,作用 点的速度为y。则瞬时功率为: N-N. a为F与之间的夹角,M,与δ方向相同时取十”,相反时取“一” 机器运动方程的一般表达式为: Fm,cosa+】 ±M,o,ld 斯世大学 INJIANG UNIVERSITY 机械设计教研室 理械
机原 理械 运动方程为: d(J1ω2 1 /2+Jc2ω2 2 /2+m2v 2 c2 /2+m3v 2 3 /2)=(M1ω1-F3 v3 )dt 推广到一般,设有n个活动构件,用Ei表示其动能。 则有: 设作用在构件i上的外力为Fi,力矩Mi为,力Fi 作用 点的速度为vi。则瞬时功率为: αi为Fi与vi之间的夹角,Mi与ωi方向相同时取“+”,相反时取“-” 机器运动方程的一般表达式为: = = n i E Ei 1 = = n i N Ni 1 = = + n i mi vi Jci i 1 2 2 ) 2 1 2 1 ( = = = + n i n i i i i Mi i Fv 1 1 cos )] 2 1 2 1 [ ( 1 2 2 = + n i i i ci i d m v J Fv M dt n i n i i i i i i [ cos ] 1 1 = = = +

2,机械的运动动方程式 二、机械系统的等效动力学模型 上例有结论: dW1o2十Je2o2十m2c22十m32)=M1—FE v:)dt 重写为 do2/2(J+Je2o22/o21十m222/o21十3o2)] =ω,M一F3y3@)dt 右边小括号内的各项具有转动惯量的量纲, 左边小括号内的各项具有力矩的量纲。 令: J(Ji十J2022o2 M=M1-F3v3/0 则有:d3Jo22=M.o,dMd② 世大学 KINJIANG UNIVERSITY 机械设计教研室
机原 理械 二、机械系统的等效动力学模型 上例有结论: d(J1ω2 1 /2+Jc2ω2 2 /2+m2v 2 c2 /2+m3v 2 3 /2) =(M1ω1-F3 v3 )dt 重写为: d[ω2 1 /2 (J1+Jc2ω2 2 /ω2 1+m2v 2 c2 /ω2 1+m3v 2 3 /ω2 1 ) ] =ω1 (M1 -F3 v3 /ω1 )dt 右边小括号内的各项具有转动惯量的量纲, 左边小括号内的各项具有力矩的量纲。 令: Je=( J1+Jc2ω2 2 /ω2 1.) M e = M1-F3 v3 /ω1 则有: d(Jeω2 1 /2 )= Meω1 dt=Medφ
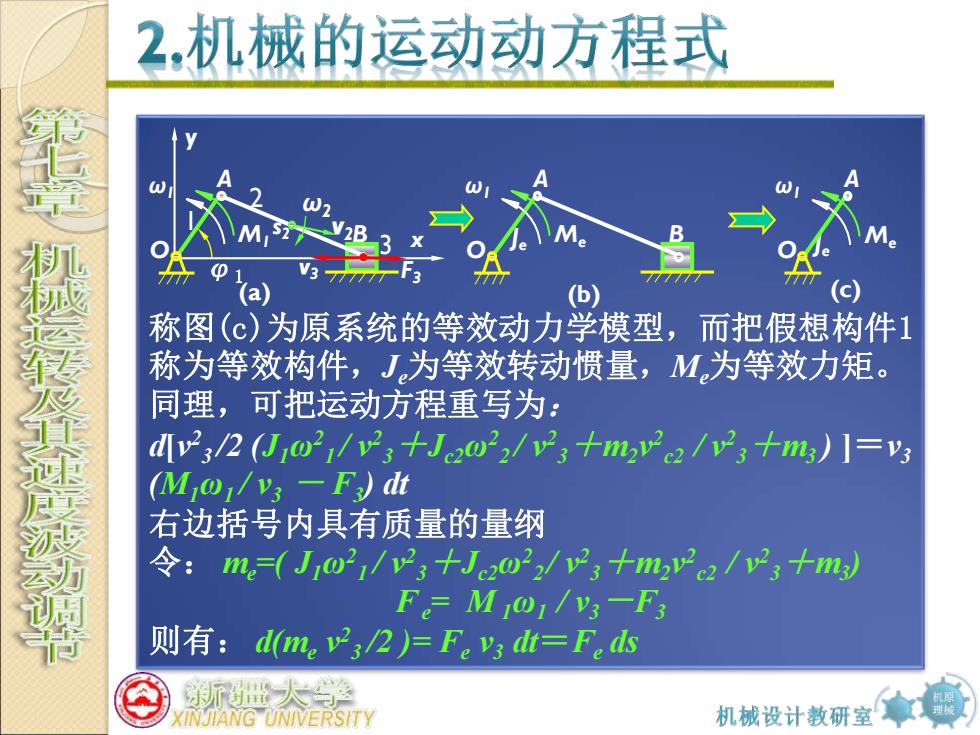
2,机械的运动动方程式 称图(c)为原系统的等效动力学模型,而把假想构件1 称为等效构件,J为等效转动惯量,M为等效力矩。 同理,可把运动方程重写为: d,2(Jo21/w2,+Je22十m2/v3十%)]=v3 (M0/v3-F)dt 右边括号内具有质量的量纲 令:m(Jo2/2十e2o2272十m22/,大m F=M9/3一F 则有:dme2,2)=F。dt=Fd INJIANG UNIVERSITY 机械设计教研室
机原 理械 称图(c)为原系统的等效动力学模型,而把假想构件1 称为等效构件,Je为等效转动惯量,Me为等效力矩。 同理,可把运动方程重写为: d[v 2 3 /2 (J1ω2 1 / v2 3+Jc2ω2 2 / v2 3+m2v 2 c2 / v2 3+m3 ) ]=v3 (M1ω1 / v3 - F3 ) dt 右边括号内具有质量的量纲 令: me=( J1ω2 1 / v2 3+Jc2ω2 2 / v2 3+m2v 2 c2 / v2 3+m3 ) Fe = M 1ω1 / v3-F3 则有: d(me v 2 3 /2 )= Fe v3 dt=Fe ds (a) (b) J x e y 1 2 3 s2 O A B φ1 ω2 M1 ω1 v2 F3 v3 O A Me B ω1 Me (c) J O e ω A 1